Сторона квадрата равна 4 см найдите длину описанной окружности

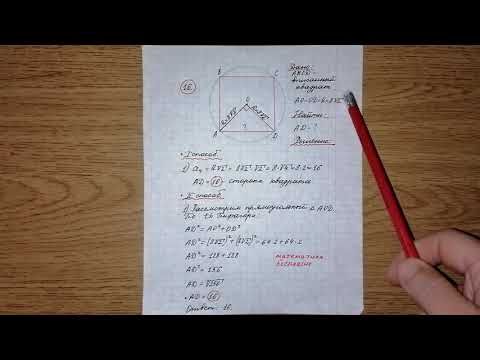
Решение:
Центр окружности лежит в центре квадрата. Проведите диагональ квадрата — она равна (корень из 2)*4 см. Если вам требуется найти диаметр, то это он и есть. Если радиус — разделите диаметр на два — получите 4/(корень из 2).

Радиусом окружности будет 1/2 диагонали квадрата. Эта диагональ — гипотенуза прямоугольного треугольника, катет которого — сторона квадрата = 4 см. Находим гипотенузу и дели ее пополам: $$ (sqrt<4^+4^>)/2 = 2sqrt $$ Длина окружности 2piR: = $$ 2*pi*2sqrt=4pisqrt $$

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Сторона квадрата равна 4 см вычислите длину длуну окружности описанной около него?

Геометрия | 5 — 9 классы

Сторона квадрата равна 4 см вычислите длину длуну окружности описанной около него.

5) [4 корень из 2]

Видео:16)Радиус окружности, описанной около квадрата, равен 8√2. Найдите длину стороны этого квадрата.Скачать

Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см?

Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Найдите полощадь круга и длину ограничивающей его окружности, если сторона квадрата , описанного около него, равна 6 см?

Найдите полощадь круга и длину ограничивающей его окружности, если сторона квадрата , описанного около него, равна 6 см.

Видео:ПОДРОБНОЕ РЕШЕНИЕ ВОСЕМНАДЦАТОГО ЗАДАНИЯ ОГЭ МАТЕМАТИКА 2018Скачать

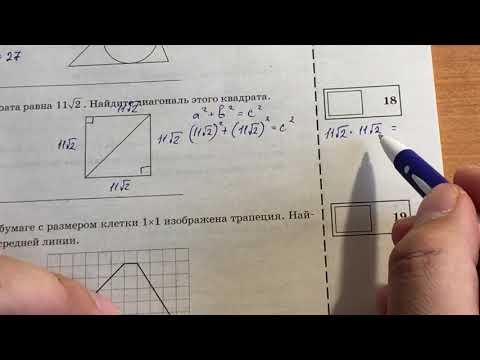
Длина окружности, описанной около квадрата, равно 8П см?

Длина окружности, описанной около квадрата, равно 8П см.

Найдите периметр квадрата.

Видео:Радиус окружности рассчитываем через длину стороны квадратаСкачать

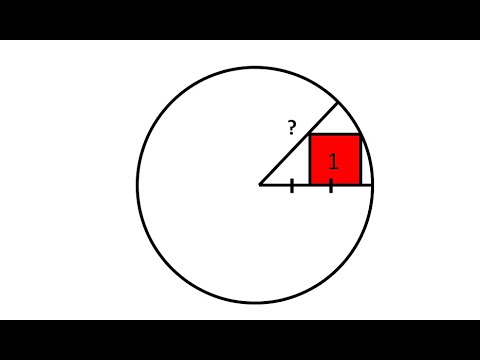
Найдите сторону квадрата описанного около окружности если сторона правильного шестиугольника вписанного в эту окружность равна 3?

Найдите сторону квадрата описанного около окружности если сторона правильного шестиугольника вписанного в эту окружность равна 3.

Видео:16 задание ОГЭ 2023 Окружность Квадрат#ShortsСкачать

Найдите длину окружности описанной около квадрата со стороной 8 сантиметров?

Найдите длину окружности описанной около квадрата со стороной 8 сантиметров.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите площадь круга и длину ограничевающнй его окружности, если сторона квадрата, описанного около него, равна 6 см?

Найдите площадь круга и длину ограничевающнй его окружности, если сторона квадрата, описанного около него, равна 6 см.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Длина окружности, описанной около квадрата, равна 12П см?

Длина окружности, описанной около квадрата, равна 12П см.

Найдите длину окружности, вписанной в квадрат.

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Длина окружности описанной около квадрата равна 4п см?

Длина окружности описанной около квадрата равна 4п см.

Найдите площадь квадрата.

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Длина окружности, описанной около квадрата, равно 8П см?

Длина окружности, описанной около квадрата, равно 8П см.

Найдите периметр квадрата.

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Найдите площадь круга и длину ограничивающей его окружности если сторона квадрата описанного около него равна 8 см?

Найдите площадь круга и длину ограничивающей его окружности если сторона квадрата описанного около него равна 8 см.

Вопрос Сторона квадрата равна 4 см вычислите длину длуну окружности описанной около него?, расположенный на этой странице сайта, относится к категории Геометрия и соответствует программе для 5 — 9 классов. Если ответ не удовлетворяет в полной мере, найдите с помощью автоматического поиска похожие вопросы, из этой же категории, или сформулируйте вопрос по-своему. Для этого ключевые фразы введите в строку поиска, нажав на кнопку, расположенную вверху страницы. Воспользуйтесь также подсказками посетителей, оставившими комментарии под вопросом.

A)y2 — 24y + 144 б)81 + 18m + m2 в)16×2 — 8xy + y2 г)169 — x2 д)36y2 + 84yn + 49n2 e) — 25s2 + 64×2.

Этих данных недостаточно. Задачу можно решить, если только ABCD — квадрат. Тогда периметр равен 7 * 4 = 28 см, а площадь — 7 * 7 = 49 см ^ 2.

DOE = AOB = 12° BOC = FOE = 69° AOF = COD = (360° — 2(12° + 69°)) : 2 = 99° BOD = BOC + COD = 69° + 99° = 168° Ответ : BOD = 168°.

MN||PK MN = PK = 10 MP : тргENK N = 60 E = 90 K = 30 NK = 2×NE NK = 2×2 NK = 4.

P = (a + b + c) / 2 = (13 + 14 + 15) / 2 = 42 / 2 = 21 По формуле Герона S = = S = R = = = = 8, 125 По теореме Пифагора SA = SB = SC = = = 8, 7.

Пусть в треугольнике ABC известны стороны AB = c, BC = b и медиана BM = m. На луче AM отложим отрезок MD, MD = AM и соединим точку D с точками B и C. Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD..

∠АВС = ∠А₁АС + ∠С₁СА ∠А₁АС = ∠С₁СА = х х + х + 130 = 180 2х + 130 = 180 2х = 180 — 130 2х = 50 х = 25 = ∠А₁АС = ∠С₁СА Тогда : ∠АВС = 25 + 25 = 50 Пусть ∠А = ∠С = у Тогда : у + у + 50 = 180 2у + 50 = 180 2у = 130 у = 65 = ∠А = ∠С ∠АА₁В = 180 — (ВАА₁ +..

Весь циферблат равен 360°. Каждые 5 минут — это 30° (360 : 12 = 30). 5 час — это отсек 25 минуты. Так же известно, что есть 10 минут. Получается, что угол занимает по три пятиминутки ((25 — 10) : 5 = 3) Узнаём градусную меру : 3•30° = 90°.

Большая дуга относится к меньшей как 4 : 1. Т. е. Большая дуга — 4 части, меньшая — 1 часть. Вся окружность — 5 частей. Градусная мера окружности 360°, откуда 1 часть = 360° : 5 = 72°. Это меньшая дуга. Большая дуга = 72 * 4 = 288°. Ответ : 72..

По теореме Пифагора : смНайдем синус угла B : sinB = AC / AB = 5 / 10 = 1 / 2значит, В = 30 градусов.

Видео:СТОРОНА КВАДРАТА через РАДИУС вписанной и описанной окружностейСкачать

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Видео:№1104. Найдите длину окружности, описанной около: а) правильного треугольника со стороной аСкачать

Свойства квадрата

• Длины всех сторон квадрата равны.
• Все углы квадрата прямые.
• Диагонали квадрата равны.
• Диагонали пересекаются под прямым углом.
• Диагонали квадрата являются биссектрисами углов.
• Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

.

(1)

Из равенства (1) найдем d:

.

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Видео:№1105. Найдите длину окружности, вписанной: а) в квадрат со стороной а; б) в равнобедренныйСкачать

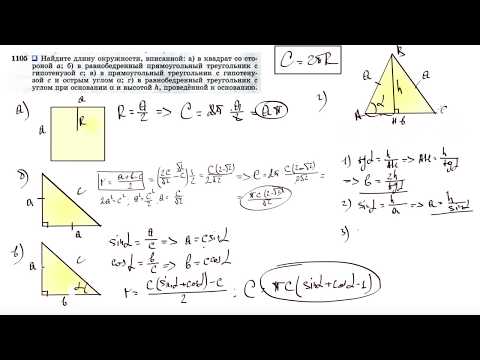
Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Видео:Длина окружности. Математика 6 класс.Скачать

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Видео:Длина окружности. Практическая часть. 9 класс.Скачать

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

.

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Видео:Найти длину стороны квадрата, вписанного интересным способомСкачать

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

.

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

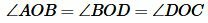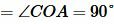(11)

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

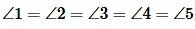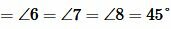(13)

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).