Запишите три плоскости заданные вершинами куба abcda1b1c1d1 и параллельные прямой aa1

Параллельность прямой плоскости.10 класс Презентация составлена для изучения темы. Будет полезна учителям и учащимся.

Просмотр содержимого документа
«Параллельность прямой плоскости»

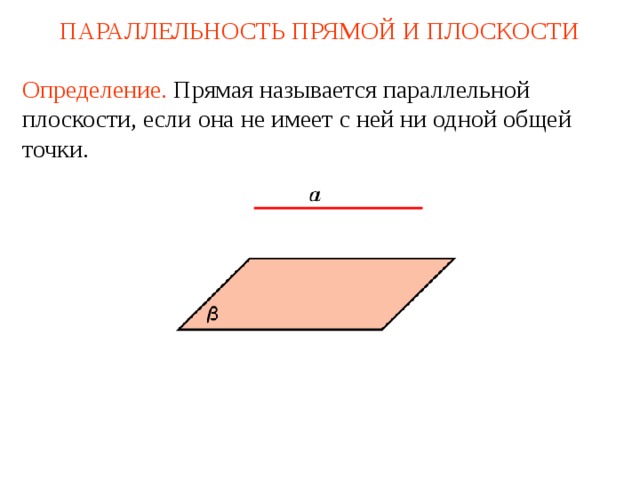
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Определение. Прямая называется параллельной плоскости, если она не имеет с ней ни одной общей точки.

В режиме слайдов формулировка появляется после кликанья мышкой

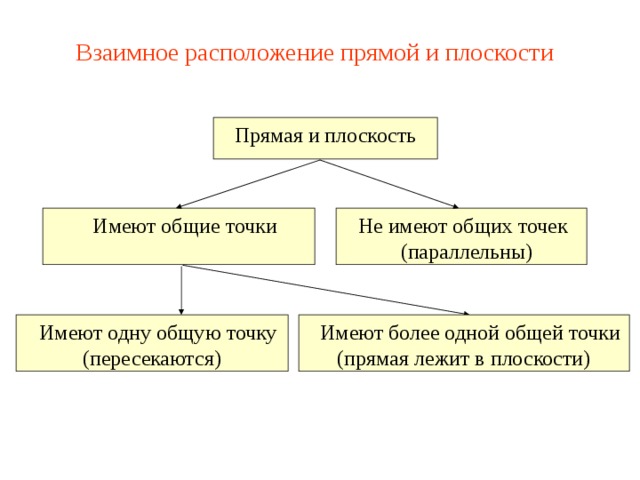
Взаимное расположение прямой и плоскости

Прямая и плоскость

Имеют общие точки

Не имеют общих точек

Имеют одну общую точку (пересекаются)

Имеют более одной общей точки (прямая лежит в плоскости)

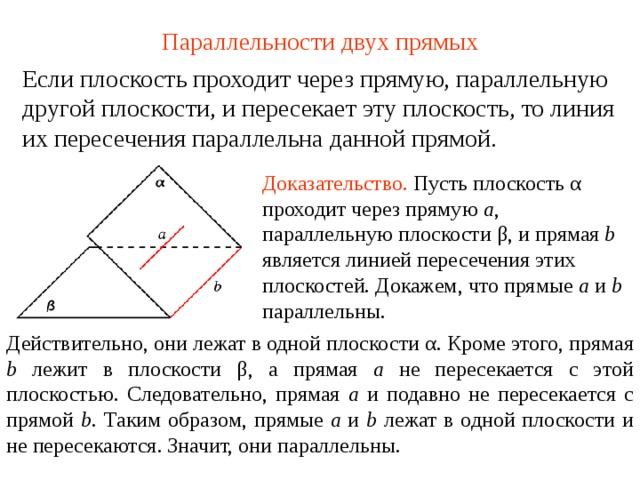
Параллельности двух прямых

Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия их пересечения параллельна данной прямой.

Доказательство. Пусть плоскость α проходит через прямую a , параллельную плоскости β , и прямая b является линией пересечения этих плоскостей. Докажем, что прямые a и b параллельны.

В режиме слайдов формулировка появляется после кликанья мышкой

Действительно, они лежат в одной плоскости α . Кроме этого, прямая b лежит в плоскости β , а прямая a не пересекается с этой плоскостью. Следовательно, прямая a и подавно не пересекается с прямой b . Таким образом, прямые a и b лежат в одной плоскости и не пересекаются. Значит, они параллельны.

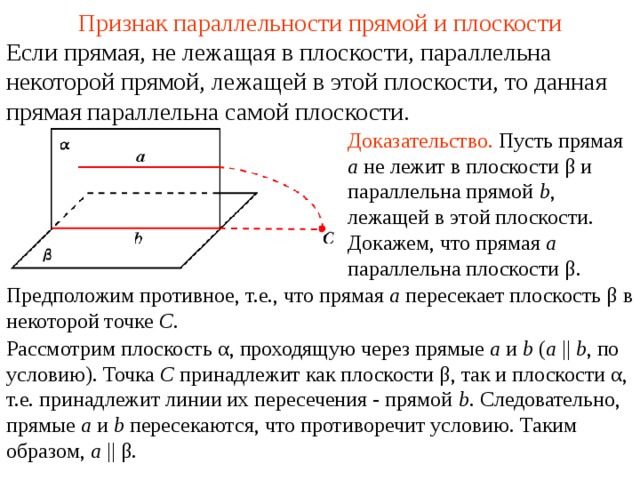
Признак параллельности прямой и плоскости

Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то данная прямая параллельна самой плоскости.

Доказательство. Пусть прямая a не лежит в плоскости β и параллельна прямой b , лежащей в этой плоскости. Докажем, что прямая a параллельна плоскости β .

Предположим противное, т.е., что прямая a пересекает плоскость β в некоторой точке C .

В режиме слайдов формулировка появляется после кликанья мышкой

Рассмотрим плоскость α , проходящую через прямые a и b ( a || b , по условию). Точка C принадлежит как плоскости β , так и плоскости α , т.е. принадлежит линии их пересечения — прямой b . Следовательно, прямые a и b пересекаются, что противоречит условию. Таким образом, a || β .

Верно ли утверждение о том, что две прямые, параллельные одной и той же плоскости, параллельны между собой?

В режиме слайдов ответ появляется после кликанья мышкой

Верно ли утверждение: «Прямая, параллельная плоскости, параллельна любой прямой, лежащей в этой плоскости»?

В режиме слайдов ответ появляется после кликанья мышкой

Одна из двух параллельных прямых параллельна плоскости. Верно ли утверждение, что и вторая прямая параллельна этой плоскости?

В режиме слайдов ответ появляется после кликанья мышкой

Даны две параллельные прямые. Через каждую из них проведена плоскость. Эти две плоскости пересекаются. Как расположена их линия пересечения относительно данных прямых?

В режиме слайдов ответ появляется после кликанья мышкой

Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым?

В режиме слайдов ответ появляется после кликанья мышкой

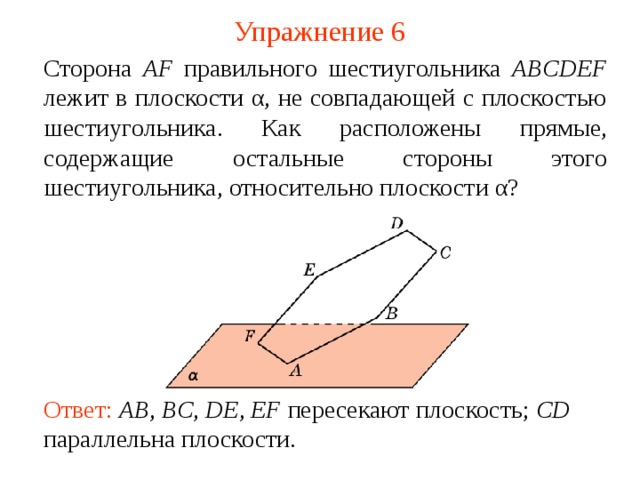
Сторона AF правильного шестиугольника ABCDEF лежит в плоскости α, не совпадающей с плоскостью шестиугольника. Как расположены прямые, содержащие остальные стороны этого шестиугольника, относительно плоскости α?

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: AB , BC , DE , EF пересекают плоскость; CD параллельна плоскости.

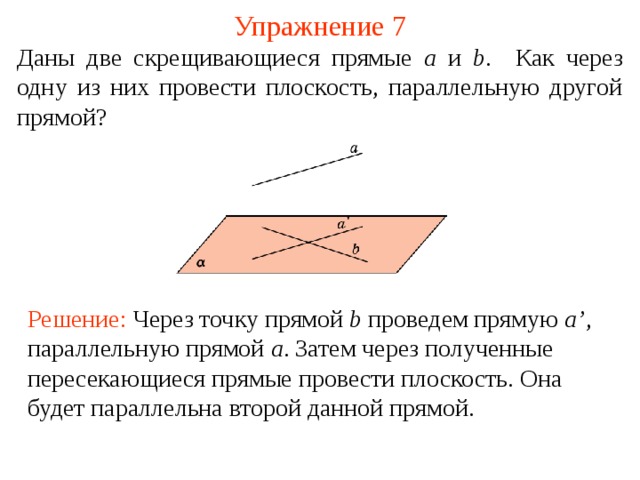
Даны две скрещивающиеся прямые a и b . Как через одну из них провести плоскость, параллельную другой прямой ?

Решение: Через точку прямой b проведем прямую a’ , параллельную прямой a . Затем через полученные пересекающиеся прямые провести плоскость. Она будет параллельна второй данной прямой.

В режиме слайдов ответ появляется после кликанья мышкой

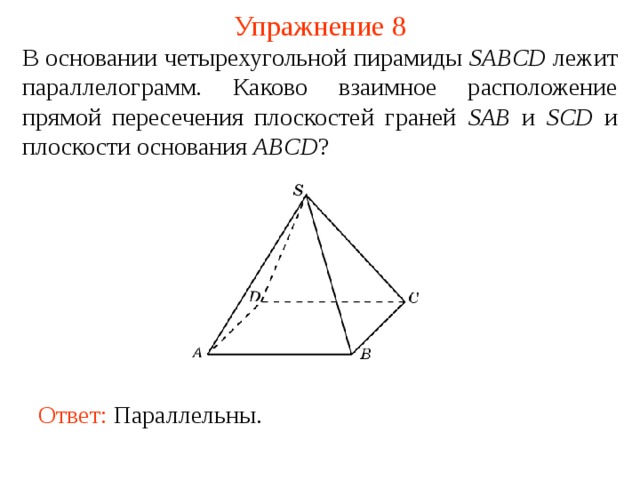
В основании четырехугольной пирамиды SABCD лежит параллелограмм. Каково взаимное расположение прямой пересечения плоскостей граней SAB и SCD и плоскости основания ABCD ?

В режиме слайдов ответ появляется после кликанья мышкой

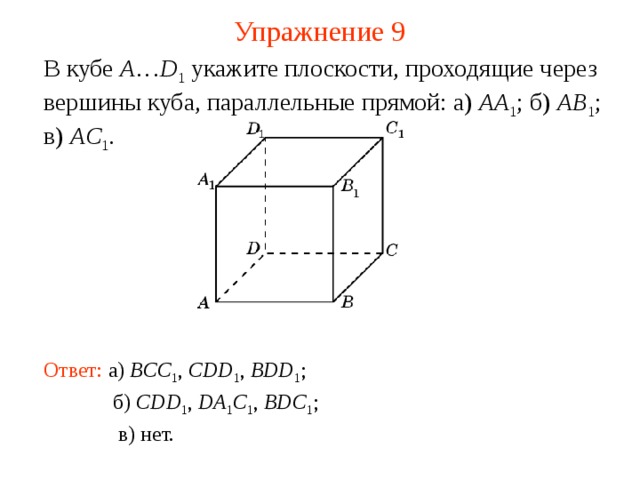
В кубе A … D 1 укажите плоскости, проходящие через вершины куба, параллельные прямой: а) AA 1 ; б) AB 1 ; в) AC 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: а ) BCC 1 , CDD 1 , BDD 1 ;

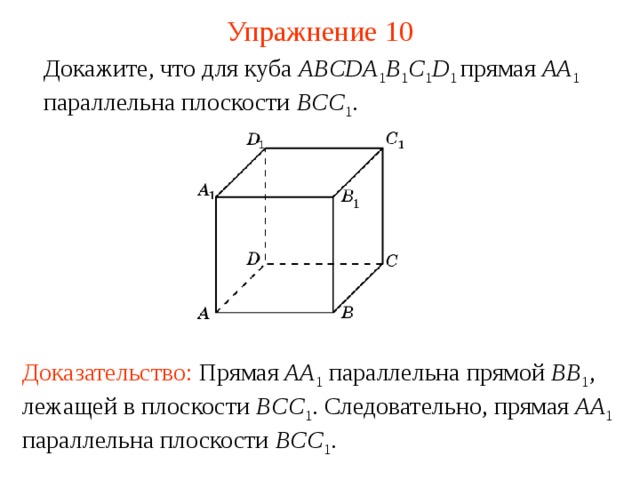
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AA 1 параллельна плоскости BCC 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AA 1 параллельна прямой BB 1 , лежащей в плоскости BCC 1 . Следовательно, прямая AA 1 параллельна плоскости BCC 1 .

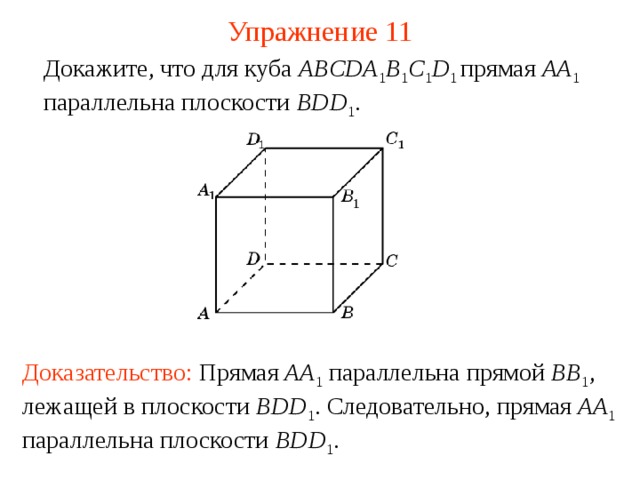
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AA 1 параллельна плоскости BDD 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AA 1 параллельна прямой BB 1 , лежащей в плоскости BDD 1 . Следовательно, прямая AA 1 параллельна плоскости BDD 1 .

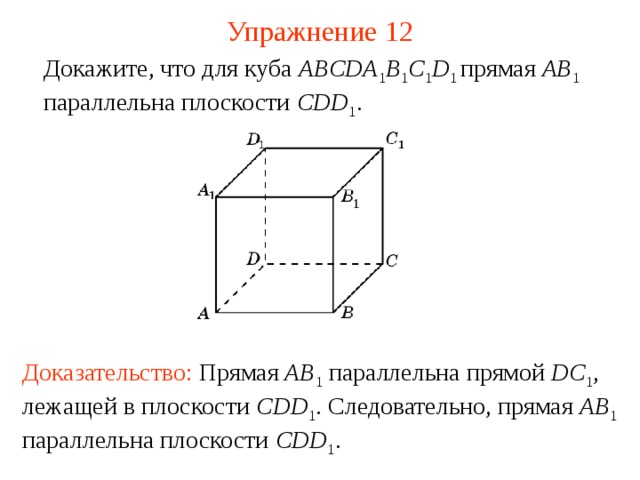
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AB 1 параллельна плоскости CDD 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AB 1 параллельна прямой DC 1 , лежащей в плоскости CDD 1 . Следовательно, прямая AB 1 параллельна плоскости CDD 1 .

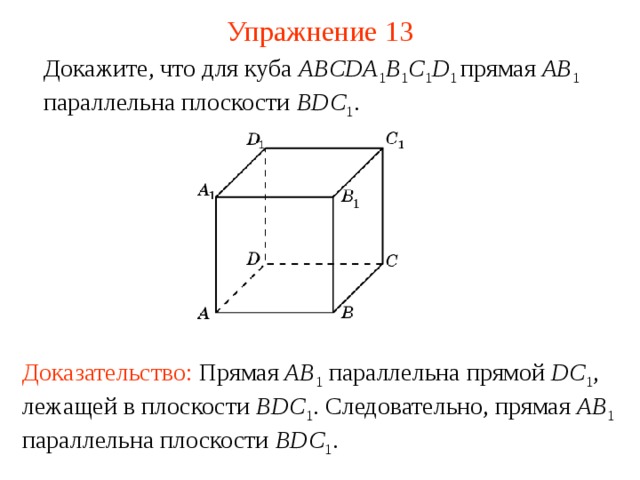
Докажите, что для куба ABCDA 1 B 1 C 1 D 1 прямая AB 1 параллельна плоскости BDC 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AB 1 параллельна прямой DC 1 , лежащей в плоскости BDC 1 . Следовательно, прямая AB 1 параллельна плоскости BDC 1 .

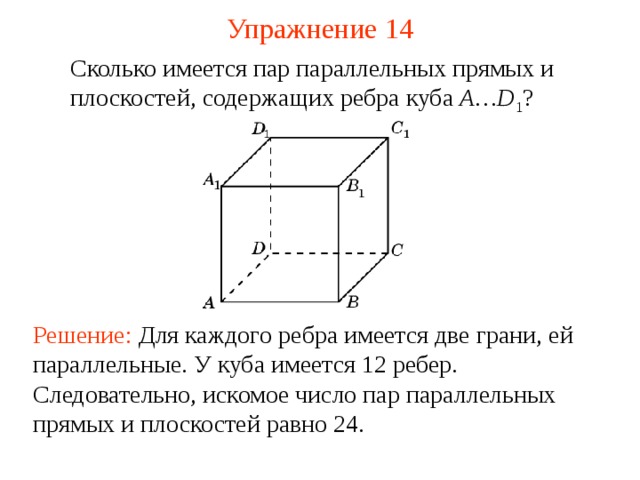
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра куба A…D 1 ?

В режиме слайдов ответ появляется после кликанья мышкой

Решение: Для каждого ребра имеется две грани, ей параллельные. У куба имеется 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24.

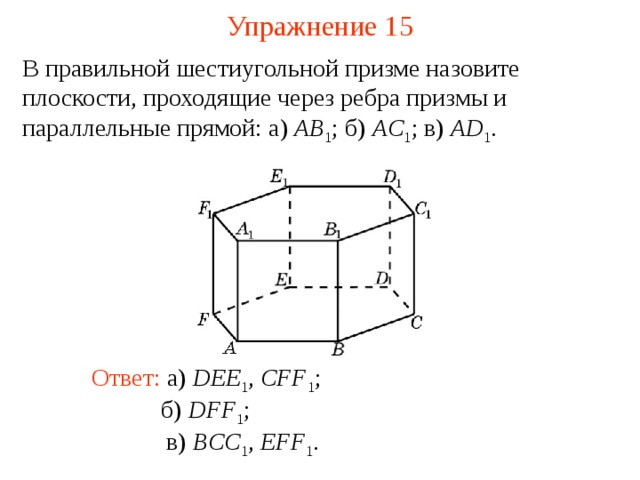
В правильной шестиугольной призме назовите плоскости, проходящие через ребра призмы и параллельные прямой: а) AB 1 ; б) AC 1 ; в) AD 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Ответ: а) DEE 1 , CFF 1 ;

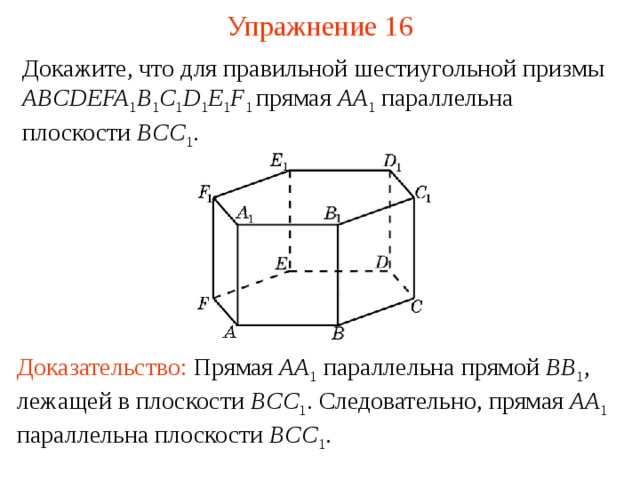
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AA 1 параллельна плоскости BCC 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AA 1 параллельна прямой BB 1 , лежащей в плоскости BCC 1 . Следовательно, прямая AA 1 параллельна плоскости BCC 1 .

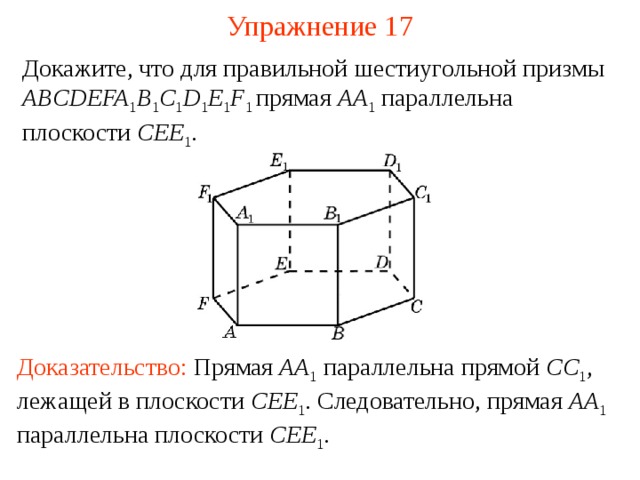
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AA 1 параллельна плоскости CEE 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AA 1 параллельна прямой CC 1 , лежащей в плоскости CEE 1 . Следовательно, прямая AA 1 параллельна плоскости CEE 1 .

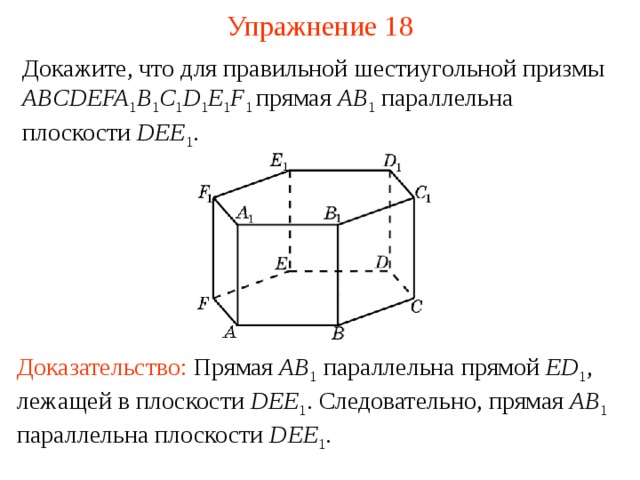
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AB 1 параллельна плоскости DEE 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AB 1 параллельна прямой ED 1 , лежащей в плоскости DEE 1 . Следовательно, прямая AB 1 параллельна плоскости DEE 1 .

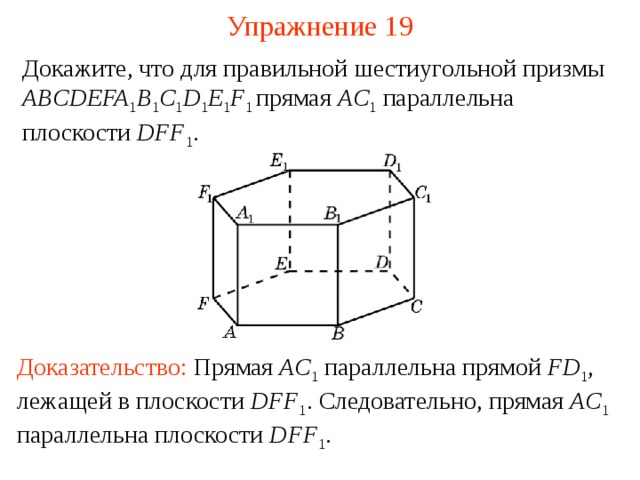
Докажите, что для правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 прямая AC 1 параллельна плоскости DFF 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AC 1 параллельна прямой FD 1 , лежащей в плоскости DFF 1 . Следовательно, прямая AC 1 параллельна плоскости DFF 1 .

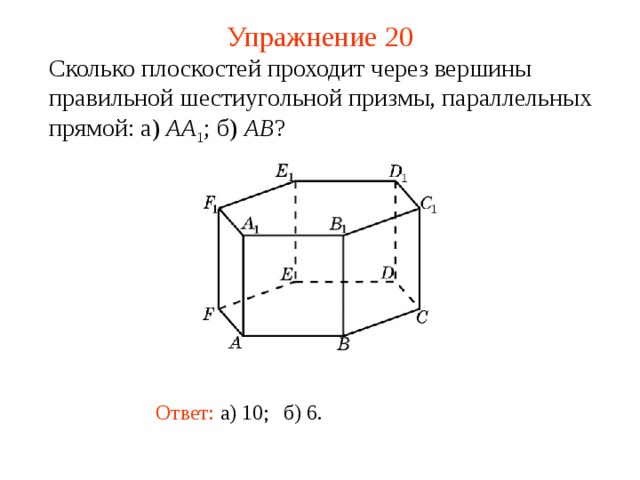
Сколько плоскостей проходит через вершины правильной шестиугольной призмы, параллельных прямой: а) AA 1 ; б) AB ?

В режиме слайдов ответ появляется после кликанья мышкой

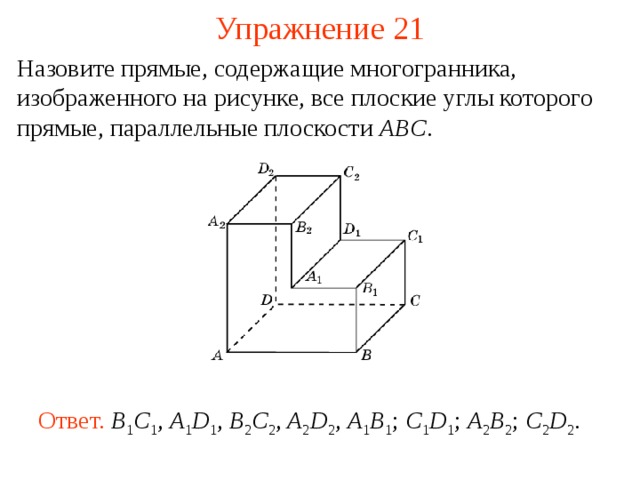
Назовите прямые, содержащие многогранника, изображенного на рисунке, все плоские углы которого прямые, параллельные плоскости ABC .

В режиме слайдов ответ появляется после кликанья мышкой

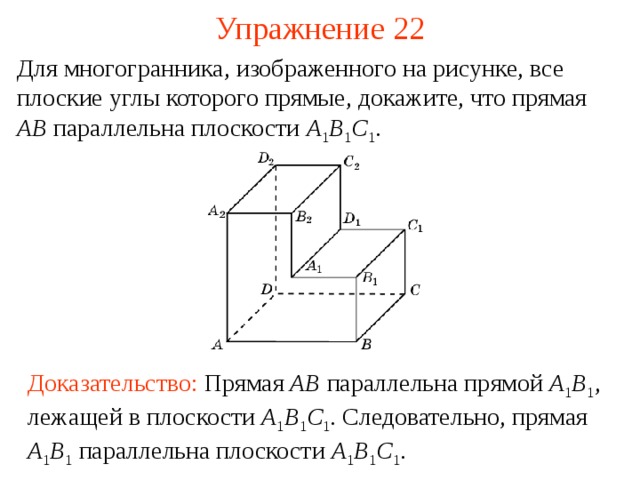
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AB параллельна плоскости A 1 B 1 C 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AB параллельна прямой A 1 B 1 , лежащей в плоскости A 1 B 1 C 1 . Следовательно, прямая A 1 B 1 параллельна плоскости A 1 B 1 C 1 .

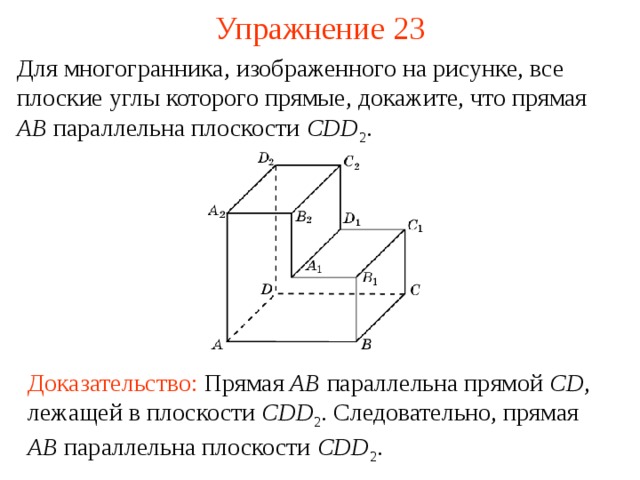
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AB параллельна плоскости CDD 2 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AB параллельна прямой CD , лежащей в плоскости CDD 2 . Следовательно, прямая AB параллельна плоскости CDD 2 .

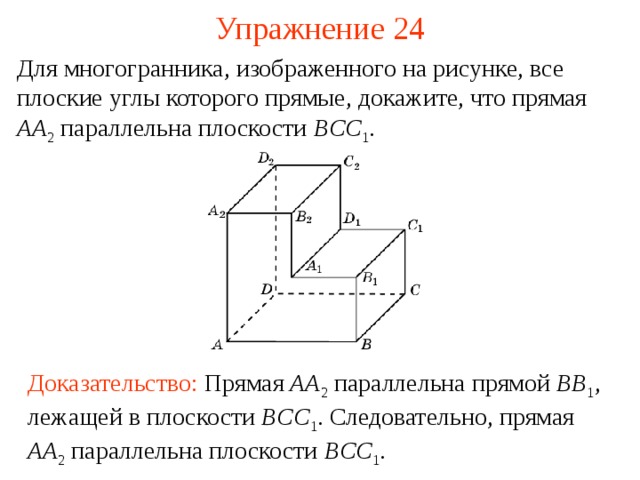
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AA 2 параллельна плоскости BCC 1 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AA 2 параллельна прямой BB 1 , лежащей в плоскости BCC 1 . Следовательно, прямая AA 2 параллельна плоскости BCC 1 .

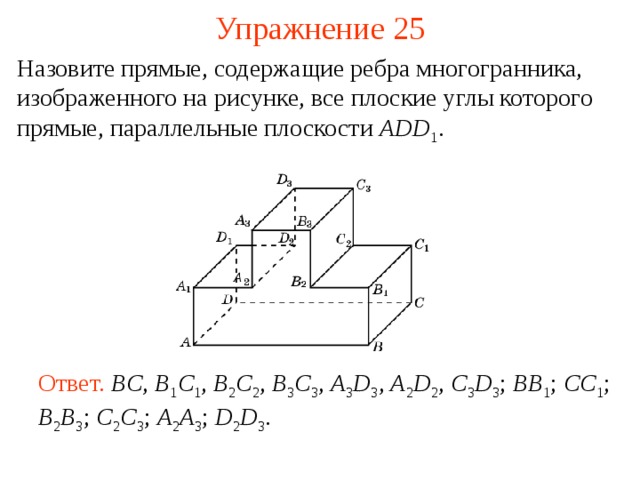
Назовите прямые, содержащие ребра многогранника, изображенного на рисунке, все плоские углы которого прямые, параллельные плоскости ADD 1 .

В режиме слайдов ответ появляется после кликанья мышкой

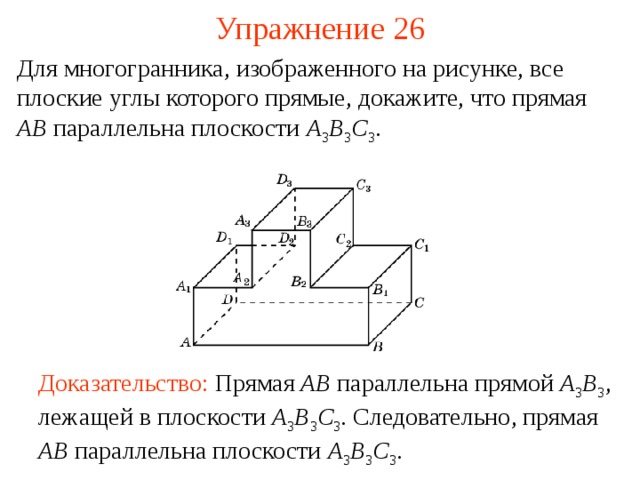
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AB параллельна плоскости A 3 B 3 C 3 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AB параллельна прямой A 3 B 3 , лежащей в плоскости A 3 B 3 C 3 . Следовательно, прямая AB параллельна плоскости A 3 B 3 C 3 .

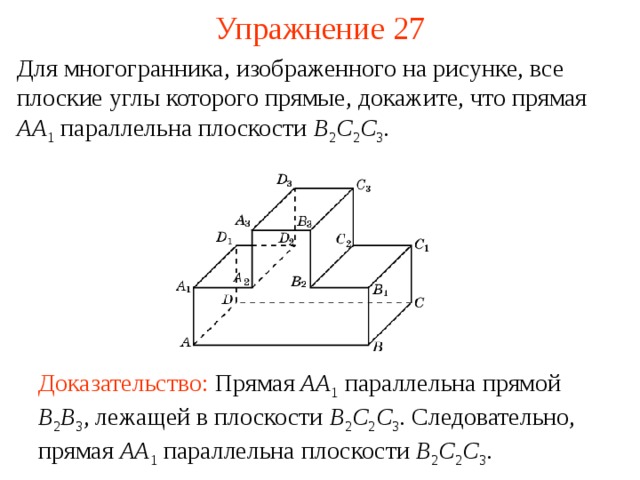
Для многогранника, изображенного на рисунке, все плоские углы которого прямые, докажите, что прямая AA 1 параллельна плоскости B 2 C 2 C 3 .

В режиме слайдов ответ появляется после кликанья мышкой

Доказательство: Прямая AA 1 параллельна прямой B 2 B 3 , лежащей в плоскости B 2 C 2 C 3 . Следовательно, прямая AA 1 параллельна плоскости B 2 C 2 C 3 .

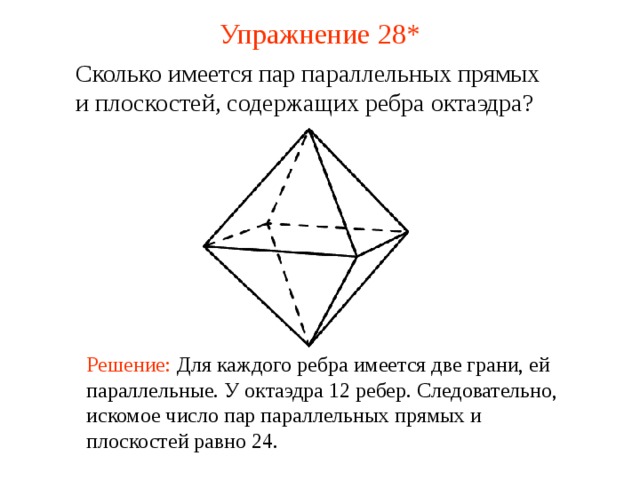
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра октаэдра?

В режиме слайдов ответ появляется после кликанья мышкой

Решение: Для каждого ребра имеется две грани, ей параллельные. У октаэдра 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24.

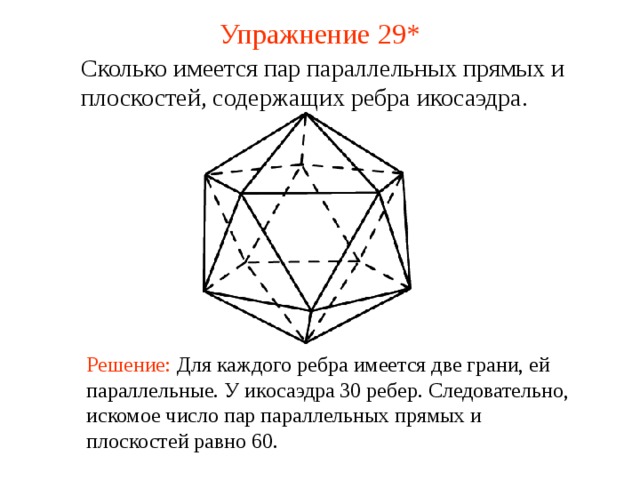
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра икосаэдра .

В режиме слайдов ответ появляется после кликанья мышкой

Решение: Для каждого ребра имеется две грани, ей параллельные. У икосаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 60.

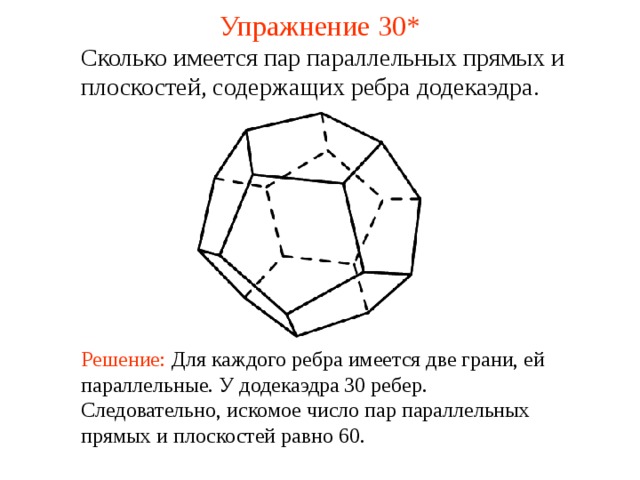
Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра додекаэдра .

В режиме слайдов ответ появляется после кликанья мышкой

Решение: Для каждого ребра имеется две грани, ей параллельные. У додекаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 60.

Видео:№196. Изобразите куб ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через:Скачать

Запишите три плоскости заданные вершинами куба abcda1b1c1d1 и параллельные прямой aa1

Ответ:

Объяснение:

AA₁ = BB₁ и AA₁║BB₁, a BB₁ = CC₁ и BB₁║CC₁ как противоположные стороны квадратов, значит

AA₁║CC₁ и АА₁ = СС₁, значит

АС ║ А₁С₁

Аналогично, A₁D₁ = BC и A₁D₁║BC, значит

A₁B║D₁C

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны.

Видео:№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать

Ход урока

Тематическое оценивание № 2 можно провести путем проведения тематической контрольной работы.

1. Тематическая контрольная работа № 2

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnlineСкачать

Вариант 1

1. Пользуясь изображением куба ABCDA 1В1 C 1 D 1 (рис. 113), запишите ребра куба, параллельные грани ABCD . (3 балла)

2. Сторона АВ треугольника АВС лежит в плоскости α , а вершина С не лежит в этой плоскости. Точки М и N — середины сторон АС и ВС соответственно. Докажите, что прямая MN параллельна плоскости α . (3 балла)

3. Даны две параллельные плоскости α и β . Точки А и В принадлежат плоскости α , точки С и D — в плоскости β . Отрезки AD и ВС пересекаются в точке М, АВ = 10 см, BM = 6 см, CM = 12 см. Найти длину отрезка CD . (3 балла)

4. Постройте сечение куба ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки А, В и D 1. (3 балла)

Вариант 2

1. Пользуясь изображением куба ABCDA 1 B 1 C 1 D 1 (рис. 114), запишите грани куба, параллельные ребру AA 1. (3 балла)

2. Две стороны данного треугольника параллельны плоскости α . Докажите, что и третья его сторона параллельна этой плоскости. (3 балла)

3. Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно и параллельна стороне АС. Найти длину отрезка MN , если АС = 24 см, а ВМ:АМ = 3:1. (3 балла)

4. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через диагональ ВС1 грани куба и параллельная диагонали АС грани куба. (3 балла)

Вариант 3

1. Пользуясь изображением прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 (рис. 115), укажите ребра, параллельные плоскости BDD 1. (3 балла)

2. Основание AD трапеции ABCD лежит в плоскости α , а точки В и С не принадлежат этой плоскости. Докажите, что прямая ВС параллельна плоскости α . (3 балла)

3. Даны две параллельные плоскости α и β . Луч SC пересекает плоскость α в точке А, а плоскость β в точке С; луч SD пересекает плоскость α в точке В, а плоскость β в точке D ; SA = 14 см, SC = 42 см, CD = 18 см. Найти длину отрезка АВ. (3 балла)

4. Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через точки В, С и A 1. (3 балла)

Вариант 4

1. Пользуясь изображением прямоугольного параллелепипеда (рис. 116), запишите грани прямоугольного параллелепипеда, параллельные прямой ВС. (3 балла)

2. Стороны данного острого угла параллельны плоскости α . Докажите, что и биссектриса этого угла параллельна этой плоскости. (3 балла)

3. Плоскость α пересекает стороны АВ и ВС треугольника АВС в точках М и N соответственно и параллельна стороне АС. Найти сторону АС треугольника, если АС — MN = 8 см, ВМ : МА = 2:1. (3 балла)

4. Постройте сечение куба ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через диагональ AD 1 грани куба и параллельная диагонали BD грани куба. ( 3 балла)

Ответ. Вариант 1. 1. А 1 В 1 , В 1 С 1 , C 1 D 1 , А 1 D 1 . 3. 20 cm . 4. ( Рис. 117 )

Вариант 2. 1. ВСС 1 В 1 , DCC 1 D 1 . 3. 18 cm . 4. ( Рис. 118 )

Вариант 3. 1. АА 1 , СС 1 . 3. 6 cm. 4. ( Рис. 119 )

Вариант 4. 1. ADD1A1, A1B1C1D1. 3. 24см. 4. ( Рис. 120 )

Вариант 1

1. Дано треугольную пирамиду SABC . Точки К, L , М — середины ребер SA , SB , SC соответственно.

а) Каково взаимное расположение прямой KL и плоскости АВС ? (2 балла)

б) Каково взаимное расположение плоскостей KLM и АВС? (2 балла)

в) Каково взаимное расположение плоскостей АВС и KLS ? (2 балла)

2. Верно ли утверждение: если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости, то эти плоскости параллельны? Ответ обоснуйте. (3 балла)

3. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 точка Р принадлежит ребру CD . Постройте сечение параллелепипеда плоскостью, проходящей через эту точку и параллельна плоскости сечения ACD 1 . (3 балла )

Вариант 2

1. Дан прямоугольный параллелепипед АВС D А 1 В 1 С 1 D 1 .

а) Каково взаимное расположение прямой А 1 В 1 и плоскости АВС ? (2 балла)

б) Каково взаимное расположение плоскостей ACD 1 и А 1 С 1 В? (2 балла)

в) Каково взаимное расположение плоскостей ACD 1 и BB 1 D 1 ? (2 балла)

2. Верно ли утверждение: если две прямые, лежащие в одной плоскости, параллельны другой плоскости, то эти плоскости параллельны? Ответ обоснуйте. (3 балла)

3. В треугольной пирамиде SABC точки Е, К, Р принадлежат ребрам АВ, SB , SC соответственно, причем РК ВС. Постройте сечение тетраэдра плоскостью ЭКР. (3 балла)

Вариант 3

1. Дано треугольную пирамиду SABC . Точки К, L , М — середины ребер SA , SB , SC соответственно.

а) Каково взаимное расположение прямой АВ и плоскости К L М ? (2 балла)

б) Каково взаимное расположение плоскостей KLM и АВС ? (2 балла)

в) Каково взаимное расположение плоскостей KLC и АВМ? (2 балла)

2. Каким может быть взаимное расположение прямых а и b , если прямая а лежит в плоскости α , а прямая b параллельна этой плоскости? Ответ обоснуйте. (3 балла)

3. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 точки К, Р, М принадлежат соответственно ребрам АА 1 , A 1 B 1 и ВС. Постройте сечение параллелепипеда плоскостью КРМ. (3 балла)

Вариант 4

1. Дан куб ABCDA 1 B 1 C 1 D 1 . Точки К, L, М — середины ребер АВ, AD , АА 1 соответственно.

а) Каково взаимное расположение прямой KL и плоскости BDC 1 ? (2 балла)

б) Каково взаимное расположение плоскостей KLM и BDA 1? (2 балла)

в) Каково взаимное расположение плоскостей KLM и BDC 1 ? (2 балла)

2. Каким может быть взаимное расположение двух прямых, если обе они параллельны одной плоскости? Ответ обоснуйте. (3 балла)

3. В тетраедрі SABC точка Е принадлежит ребру АС. Постройте сечение тетраэдра плоскостью, проходящей через точку Е и параллельная ребрам AD и ВС. Определите вид сечения. (3 балла)

Тематическое оценивание № 2 можно провести с помощью теста, тексты которого представлен ниже.

При оценивании выполнения тестов учитываются только те шесть из выполненных заданий, которым соответствует наибольшее количество баллов.

Параллельность прямых и плоскостей

Цель данного теста — проверить, умеет ли учащийся:

— изображать и находить на рисунках прямые, пересекающие плоскость и параллельные ей;

— решать задачи, используя признак параллельности прямой и плоскости;

— изображать и находить на рисунках параллельные плоскости и плоскости, которые пересекаются;

— решать задачи на взаимное расположение плоскостей, используя соответствующие свойства и признаки.

Видео:№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

Вариант 1

И уровень

1. Дано изображение прямоугольного параллелепипеда (рис. 121). Какая из указанных плоскостей параллельна прямой С D ? (1 балл)

a) AA 1 D ; б) ABB 1; в) ВВ1 D 1; г) AD 1 C.

2. Дано изображение куба ABCDA 1 B 1 C 1 D 1 (рис. 122). Какая из указанных плоскостей параллельна плоскости BDA 1? (1 балл)

а) В1 D 1А; б) АСВ1; в) А1С1 D 1; г) В1 D 1С.

3. Точки К, L , М — середины ребер SA , SB , SC тетраэдра SABC (рис. 123). Каково взаимное расположение плоскостей АВС и KLM ? (1 балл)

а) Пересекаются; б) совпадают; в) параллельны; г) определить невозможно.

1. Отрезок АВ не пересекает плоскость α , С — середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость соответственно в точках А1, В1, С1 . (рис. 124). Найдите АА1, если ВВ1 = 4 cm ; CC 1 = 3 см. ( 1 балл)

а) 1 см; б) 2 см; в) 3 см; г) 4 см.

2. Плоскость α пересекает стороны АВ и АС треугольника АВС соответственно в точках В 1 и С 1 , ВС || α (рис. 125). Найдите ВС, если В 1 С 1 = 1 см, ВВ 1 : 1 А = 3:1. (1 балл)

а) 1 см; б) 2 см; в) 3 см; г) 4 см .

3. Даны плоскость α и точка А вне ее. Сколько существует различных прямых, проходящих через точку А и параллельные α ? ( 1 балл)

а) Одна; б) ни одной; в) две; г) множество.

III уровень

1. Точки К, L , М, N являются серединами соответственно ребер SA , ВА, ВС, SC тетраэдра SABC . Найдите периметр четырехугольника KLMN , если АС = m , SB = n . (2 балла)

а) 2 m ; 6) 2 n ; в) m + n ; г) .

2. В пространстве даны две параллельные прямые а и b , а также точку А, не принадлежащую им. Сколько существует плоскостей, проходящих через точку А и параллельные прямым а и b ? (2 балла)

а) Одна; б) ни одной; в) две; г) множество.

3. Какие из указанных фигур могут быть параллельной проекцией трапеции? (2 балла)

а) Квадрат; б) трапеция; в) ромб; г) треугольник.

1. АВС D А 1 В 1 С 1 D 1 — куб, К — середина ребра СС 1 . Определить число сторон сечения куба плоскостью, проходящей через точки В, К, А. (3 балла)

а) 3; б) 4; в) 5; г) 6.

2. Какую фигуру образуют все отрезки, соединяющие любые точки двух мимобіжних отрезков? (3 балла)

а) Четырехугольник; б) плоскость; в) тетраэдр; г) отрезок.

3. ABCD — квадрат со стороной 6 см. Точка S удалена от каждой вершины квадрата на 7 см. Найдите расстояние от середины отрезка SA до середин сторон квадрата. (3 балла)

а) 2,5 см; б) 3,5 см; в) 4,5 см; г) 5,5 см.

Видео:Как строить сечения параллелепипедаСкачать

Вариант 2

1. Дано изображение тетраэдра SABC (рис. 126). Точки К, L — середины ребер SA и SB . Какая из указанных плоскостей параллельна прямой KL ? (1 балл)

a ) SAC ; б) SAB ; в) SBC ; г) АВС.

2. Дано изображение прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 (рис. 127). Какая из указанных плоскостей параллельна плоскости АВС? ( 1 балл)

a ) BDC 1 ; б) А 1 В 1 С 1 ; в) BCD ; г) DCC 1 .

3. Дано изображение куба ABCDA 1 B 1 C 1 D 1 (рис. 128). Каково взаимное расположение плоскостей АСВ 1 и A 1 C 1 D ? (1 балл)

а) Пересекаются; б) совпадают; в) параллельны; г) определить невозможно.

II уровень

1. Отрезок АВ не пересекает плоскость α , С — середина отрезка АВ. Через точки А, В, С проведены параллельные прямые, пересекающие плоскость соответственно в точках А1, В1, С1 (рис. 129). Найдите СС1, если АА1 = 2 см; ВВ1 = 4 см. (1 балл)

а) 4 см; б) 3 см; в) 2 см ; г) 1 см .

2. Плоскость α пересекает стороны АВ и АС треугольника АВС соответственно в точках В1 и С1, ВС || α (рис. 130). Найдите АС, если АС1 = 2 см, ВС:В1С1=2:1. (1 балл)

а) 1 см; б) 2 см; в) 3 см; г) 4 см.

3. Даны плоскость α и точка А вне ее. Сколько существует плоскостей, проходящих через точку А и параллельные α? (1 балл)

а) Одна; б) ни одной; в) две; r) множество.

III уровень

1. Точки К, L , М, N являются серединами соответственно ребер SA , АС, ВС, BS тетраэдра SABC . Найдите периметр четырехугольника KLMN , если каждое ребро тетраэдра равно а. (2 балла)

а) а; б) 2а; в) 3; г) 4а.

2. В пространстве даны две скрещивающиеся прямые а и b и точку А, не принадлежащую им. Сколько существует плоскостей, проходящих через точку А и параллельные прямым а и b ? (2 балла)

а) Одна; б) ни одной; в) две; г) множество.

3. Какие из указанных фигур могут быть параллельной проекцией прямоугольника? (2 балла)

а) Квадрат; б) трапеция; в) ромб; г) треугольник.

IV уровень

1. ABCDA 1 B 1 C 1 D 1 — куб, К — середина ребра СС1. Определить число сторон сечения куба плоскостью, проходящей через точки А, В1, К. (3 балла)

а) 3; б) 4; в) 5; r) 6.

2. Прямые а и b — скрещивающиеся. Найдите геометрическое место точек, образованное прямыми, каждая из которых пересекает прямую b и параллельна прямой а. (3 балла)

а) Прямая; б) плоскость; в) тетраэдр; г) отрезок.

3. Три параллельные плоскости пересекают две скрещивающиеся прямые в точках А1, А2, А3 и В1, В2, В3. Известно, что А1А2 = 4 см, В2В3 = 9 см, А2А3 = В1В2. Найдите длину отрезка А1А3. (3 балла)

💡 Видео

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и В1D1. Ответ дайте в градусах.Скачать

СЕЧЕНИЕ КУБА ПЛОСКОСТЬЮ ПРОХОДЯЩЕЙ ЧЕРЕЗ ТРИ ТОЧКИ. ЗАДАЧИ ПО СТЕРЕОМЕТРИИСкачать

Как строить сеченияСкачать

№364. Точка К—середина ребра В1С1 куба ABCDA1B1C1D1. Разложите вектор АК по векторам а = АВ,Скачать

🔥Как строить сечения куба, параллелепипеда через заданные точки?Скачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Построение сечения куба по трем точкамСкачать

Построение сечения кубаСкачать

ЕГЭ математика СТЕРЕОМЕТРИЯ 8#13🔴Скачать

#3. КАК СТРОИТЬ СЕЧЕНИЯ МНОГОГРАННИКОВ?Скачать

10 класс, 24 урок, Прямоугольный параллелепипедСкачать

Задачи на куб. Диагональ куба - bezbotvyСкачать

Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать