Задано целое число n и целочисленный вектор повторить каждый элемент вектора n раз в матлаб (8 видео)

Как писать векторизованные функции в MATLAB

Я только изучаю MATLAB, и мне трудно понять коэффициенты производительности циклов против векторизованных функций.

в моем предыдущем вопросе:вложенные циклы for очень медленно в MATLAB (предварительно) я понял, что использование векторизованной функции против 4 вложенных циклов сделало 7X раз разница во времени выполнения.

в этом примере вместо зацикливания всех измерений 4-мерного массива и вычисления медиана для каждого вектора было намного чище и быстрее просто вызвать медиану(stack, n), где n означало рабочее измерение медианной функции.

но медиана-это просто очень простой пример и мне просто повезло что это реализован параметр dimension.

мой вопрос в том, что как вы сами пишете функцию, которая работает так же эффективно, как и та, которая имеет этот диапазон измерений реализовано?

например, у вас есть функция my_median_1D который работает только на 1-D векторе и возвращает число.

как вы пишете функцию my_median_nD который действует как медиана MATLAB, принимая n-мерный массив и «рабочий размер»

Содержание

4 ответов
векторизация
MEX-files
колонка-главный заказ
как изменить порядок в векторах в Matlab
Создать массив нулей в MATLAB
1. Создание массива нулей вручную
2. Создание массива нулей с помощью встроенной функции (zeros ())
Создание (nxn) матрицы нулей
Создание массива нулей (sz1 by sz2 by- …….-Szn)
Создание матрицы определенного размера
Создание указанных типов данных нулей
Создание матрицы с использованием прототипа массива
🔥 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

4 ответов

обновление 2 (чтобы ответить на ваш обновленный вопрос)

MATLAB оптимизирован для работы с массивами. Как только вы привыкнете к этому, на самом деле очень приятно просто ввести одну строку и заставить MATLAB сделать полный 4D-цикл, не беспокоясь об этом. MATLAB часто используется для прототипирования / одноразовых вычислений, поэтому имеет смысл сэкономить время для кодирования человека и отказаться от некоторых C [++ / #] гибкость.

вот почему MATLAB внутренне делает некоторые петли очень хорошо — часто путем кодирования их как скомпилированной функции.

фрагмент кода, который вы даете на самом деле не содержит соответствующей строки кода, которая выполняет основную работу, а именно

другими словами, код, который вы показываете, должен только получить доступ к медианным значениям по их правильному индексу в теперь отсортированном многомерном массиве x (что не занимает много времени). Фактическая работа с доступом ко всем элементам массива была выполнена sort , который является встроенной (т. е. скомпилированной и высоко оптимизированной) функцией.

оригинальный ответ (о том, как построить свои собственные быстрые функции, работающие на массивах)

на самом деле существует довольно много встроенных модулей, которые принимают параметр измерения: min(stack, [], n) , max(stack, [], n) , mean(stack, n) , std(stack, [], n) , median(stack,n) , sum(stack, n) . вместе с тем, что другие встроенные функции как exp() , sin() автоматически работать над каждым элементом всего массива (т. е. sin(stack) автоматически делает четыре вложенных цикла для вас, если stack is 4D),вы можете создать много функций, которые вам могут понадобиться, просто полагаясь на существующие встроенные.

если этого недостаточно для конкретного случая, вы должны взглянуть на repmat , bsxfun , arrayfun и accumarray которые являются очень мощными функциями для выполнения вещей «путь MATLAB». Просто найдите на SO вопросы (а точнее ответы) используя один of эти, я много узнал о сильных сторонах MATLABs таким образом.

как пример, скажем, вы хотели реализовать п-норма стека вдоль измерения n , вы могли бы написать

. где вы эффективно повторно используете «что-измерение емкости» sum .

обновление

как указывает Макс в комментариях, также посмотрите на Колон оператор ( : ) который является очень мощным инструментом для выбора элементов из массива (или даже изменения его формы, что в целом делается с reshape ).

в общем, взгляните на раздел Работа С Массивами в справке-он содержит repmat et al. упоминалось выше, но и cumsum и некоторые более неясные вспомогательные функции, которые вы должны использовать в качестве строительных блоков.

не могли бы вы объяснить мне, почему этот код настолько эффективен по сравнению с простыми вложенными циклами? Вложенные циклы как и другие функции.

проблема с вложенными циклами-это не сами вложенные циклы. Это операции, которые вы выполняете внутри.

каждый вызов функции (особенно для не встроенной функции) генерирует немного накладных расходов; тем более, если функция выполняет, например, проверку ошибок, которая занимает столько же независимо от размера входных данных. Таким образом, если функция имеет только 1 мс накладных расходов, если вы вызываете его 1000 раз, вы потеряете секунду. Если вы можете вызвать его один раз для выполнения векторизованного расчета, вы платите накладные расходы только один раз.

кроме того,JIT компилятор (pdf) может помочь векторизировать простой for-loops, где вы, например, выполняете только основные арифметические операции. Таким образом, петли с простыми вычислениями в вашем посте ускоряются на много, в то время как петли, вызывающие median нет.

векторизация

в дополнение к тому, что уже было сказано, вы также должны понять, что векторизация включает в себя распараллеливание, т. е. выполнение параллельных операций с данными в отличие от последовательного выполнения (например, инструкции SIMD) и даже использование потоков и мультипроцессоров в некоторых случаях.

MEX-files

теперь, хотя пункт» интерпретированный против скомпилированный » уже был аргументирован, никто не упомянул, что вы можно расширить MATLAB, написав MEX-файлы, которые скомпилированы исполняемыми файлами, написанными на C, которые можно вызвать непосредственно как нормальную функцию изнутри MATLAB. Это позволяет реализовать критически важные для производительности части, используя язык более низкого уровня, такой как C.

колонка-главный заказ

наконец, при попытке оптимизировать некоторый код всегда помните,что MATLAB хранит матрицы в порядке столбцов. Доступ к элементам в этом порядке может привести к значительным улучшениям по сравнению с другими произвольный порядок.

например, в вашем предыдущем связанном вопросе вы вычисляли median набора сложенных изображений вдоль некоторого измерения. Теперь порядок, в котором эти размеры упорядочены, сильно влияет на производительность. Иллюстрация:

разница во времени была огромной:

но с общей функцией вы можете попробовать разбить свой массив на mat2cell (который может работать с N-D массивами, а не только матрицами) и применять ваш через cellfun . Ниже я буду использовать median в качестве примера, чтобы показать, что вы получаете эквивалентные результаты, но вместо этого вы можете передать ему любую функцию, определенную в m-файле, или анонимную функцию, определенную с помощью @(args) нотации.

Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

как изменить порядок в векторах в Matlab

У меня есть вектор

Я хочу, чтобы это было похоже

Я пробовал с H (:), но это не сработает, есть 17 нулей и 16 единиц, что может быть проблема?

Если вы хотите чередовать элементы:

Объяснение:

[1:2:end,2:2:end] , если H2 равна той же длине, что и H, создает серию индексов, которые также имеют одинаковую длину вектора H. Если вы вызываете 2:2:end и end (последний элемент) является нечетным, он эквивалентен 2:2:(end-1) , поэтому нам не нужно беспокоиться о том, что end элемент в два раза.

Для вашего вектора это выглядит как [1,3,5. 33,2,4,6. 32]

Тогда для каждого элемента из H мы присваиваем его элементу H2, представленному этим индексным вектором. То есть вторая строка сообщает MATLAB, что мы хотим, чтобы H2(1) = H(1) , H2(3) = H(2) и так далее.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Создать массив нулей в MATLAB

MATLAB обычно хранит свои переменные в матричной форме, а также в виде массива и вектора. Иногда нам часто требуется матрица (или массив, или вектор) нуля (ов) для некоторых конкретных операций. Мы можем создать матрицу нулей (ей) вручную или с помощью встроенной функции MATLAB. Встроенная функция, которая используется для создания массива или матрицы нулей (ей), называется функцией zeros (). Обычно мы предпочитаем эту встроенную функцию для простоты задачи, а не создавать массив нулей вручную. Следующая часть содержит два метода создания массива или матрицы нулей.

Видео:Умножение вектора на число. 9 класс.Скачать

1. Создание массива нулей вручную

Если мы хотим создать массив нулей, мы можем просто сделать это вручную, используя следующий код:

Matlab

По сути, это вектор-строка размером 1X5, а также массив из 5 нулей.

Создание вектора-столбца вручную: если мы хотим создать вектор-столбец, мы можем просто использовать следующий код:

Matlab

По сути, он создает вектор-столбец размером 5X1.

Создание (nxm) матрицы нулей: В этом разделе мы собираемся создать размерную матрицу (nxm). Например, пусть n = 3 и m = 4. По сути, следующая строка кода сгенерирует матрицу с 3 строками и 4 столбцами.

Matlab

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

2. Создание массива нулей с помощью встроенной функции (zeros ())

Есть несколько матриц и массивов, которые мы можем создать с помощью функции zeros (). Мы собираемся подробно описать каждый из них в следующем разделе:

Создание скалярного нуля

Синтаксис: имя_переменной = нули

Возвращаемое значение: в этом случае возвращаемое значение — только скалярный ноль («0»).

Matlab

Создание (nxn) матрицы нулей

синтаксис: matrix = zeros (n) // Здесь n — размер матрицы.

Возвращаемое значение: функция zeros (n) возвращает матрицу нулей (nxn):

Размер квадратной матрицы, заданной как целое число.
Если n равно 0, возвращается пустая матрица.
Если n отрицательно, он также возвращает пустую матрицу.

Matlab

Этот код возвращает матрицу нулей 3×3.

Создание массива нулей (sz1 by sz2 by- …….-Szn)

синтаксис: матрица = нули (sz1, sz2, ……., szn)

Возвращаемое значение: эта функция возвращает массив нулей размером sz1 на… на szN, где sz1,…, szN указывают размер каждого измерения. Например, zeros (2, 3, 4) возвращает матрицу нулей 2 X 3 X 4.

Все входные аргументы указаны как целое число.
Если любой из аргументов равен 0, возвращается пустая матрица.
Если какой-либо из аргументов отрицательный, он обрабатывается как 0.
За пределами второго измерения zeros () игнорирует конечные измерения с размером 1. Например, нули (4,1,1, 1) создают вектор нулей 4 на 1.

Matlab

Приведенный выше код создает массив нулей размером 2 на 3 на 4.

Создание матрицы определенного размера

Синтаксис: matrix = zeros (sz) // Здесь sz — размер матрицы в форме [mn].

Возвращаемое значение: возвращает массив нулей, где вектор размера sz определяет размер (матрицу). Например, нули ([2 3]) возвращают матрицу 2 на 3.

Размер каждого измерения, заданного как вектор-строка целочисленных значений. Остальные характеристики этого синтаксиса такие же, как и у предыдущего.

Matlab

% MATLAB Code for clone the size of

% another matrix

matrix = zeros([2 3])

Или мы также можем клонировать размер другой матрицы, например:

Matlab

Приведенный выше код в основном возвращает матрицу 2 X 3 с нулями в качестве каждого элемента.

Создание указанных типов данных нулей

синтаксис: matrix = zeros (___, typename) // Здесь первым аргументом может быть любой из предыдущих типов.

Возвращаемое значение: возвращает массив нулей указанного типа данных с именем typename.

Тип данных (класс) для создания, указанный как ’double’, ’single’, ’logic’, ’int8′, ’uint8′, ’int16′, ’uint16′, ’int32′, ’uint32′, ’int64′, uint64 или имя другого класса, который поддерживает нули.

Matlab

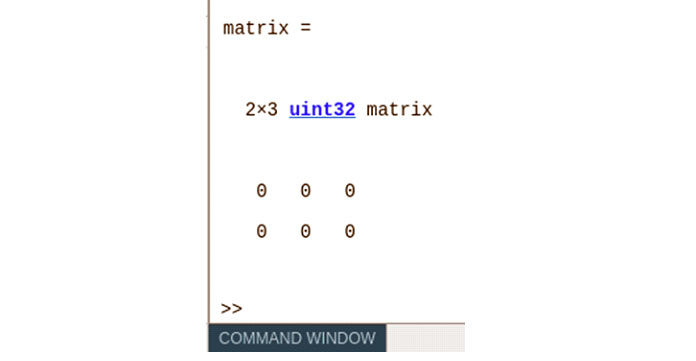
Этот код создает матрицу размером 2 на 3 с типом данных uint32.

Создание матрицы с использованием прототипа массива

синтаксис: matrix = zeros (___, ’like’, p) // Здесь первым аргументом может быть любой из предыдущих типов.

Возвращаемое значение: возвращает массив нулей, например p; т. е. того же типа данных (класса), разреженности и сложности (реальной или сложной), что и p. Пользователь может указать typename или like, но не то и другое одновременно.

Прототип создаваемого массива, заданного как массив.