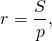Что такое вписанная окружность?Какими свойствами она обладает?
Вписанная в выпуклый многоугольник окружность — это окружность, которая касается всех сторон этого многоугольника (то есть каждая из сторон многоугольника является для окружности касательной).
Центр вписанной окружности лежит внутри многоугольника.
Многоугольник, в который вписана окружность, называется описанным.
В выпуклый многоугольник можно вписать окружность, если биссектрисы всех его внутренних углов пересекаются в одной точке.
Центр вписанной в многоугольник окружности — точка пересечения его биссектрис.
Центр вписанной окружности равноудален от сторон многоугольника. Расстояние от центра до любой стороны равно радиусу вписанной окружности (По свойству касательной, сторона описанного многоугольника перпендикулярна радиусу, проведённому в точку касания).
По свойству касательных, проведённых из одной точки, любая вершина описанного многоугольника равноудалена от точек касания, лежащих на сторонах, выходящих из этой вершины.
Окружность с центром в точке O и радиусом r вписана в пятиугольник ABCDE.
ABCDE — описанный пятиугольник.
O — точка пересечения биссектрис ABCD, то есть ∠EAO=∠BAO, ∠ABO=∠CBO, ∠BCO=∠DCO, ∠CDO=∠EDO, ∠AEO=∠DEO.
Точка O равноудалена от точек касания. Расстояние от точки O до любой из сторон равно радиусу: OK=OL=ON=OM=OP=r.
Вершины ABCDE равноудалены от соответствующих точек касания:
AM=AN, BN=BL, CL=CK, DK=DP, EP=EM.
В любой треугольник можно вписать окружность. Центр вписанной в треугольник окружности называется инцентром.
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. В частности, в трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон.
В любой правильный многоугольник можно вписать окружность. Около любого правильного многоугольника можно также описать окружность. Центр вписанной и описанной окружностей лежат в центре правильного многоугольника.
Для любого описанного многоугольника радиус вписанной окружности может быть найден по формуле
где S — площадь многоугольника, p — его полупериметр.
Кроме основной, существуют формулы для нахождения радиуса вписанной окружности в частных случаях (для правильных многоугольников, отдельных видов треугольников, трапеции, ромба и т.д.).
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать
Описанная и вписанная окружность
теория по математике 📈 планиметрия
Видео:Окружность, вписанная в правильный многоугольник | Геометрия 7-9 класс #106 | ИнфоурокСкачать
Описанная окружность
Окружность называется описанной вокруг многоугольника, если все вершины многоугольника принадлежат этой окружности. Многоугольник в этом случае называется вписанным в окружность.
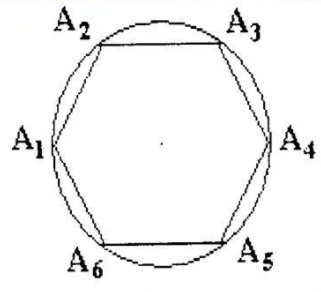
Любой правильный многоугольник можно вписать в окружность. На рисунке описанная окружность проходит через каждую вершину правильного шестиугольника.
Видео:9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать
Вписанная окружность
Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в этом случае называется описанным около окружности.
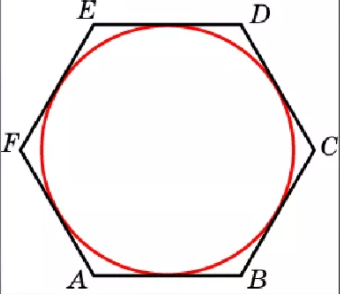
В любой правильный многоугольник можно вписать окружность. На рисунке окружность вписана в правильный шестиугольник, она касается всех его сторон.
Вписанный и описанный треугольники
Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
В любой треугольник можно вписать окружность: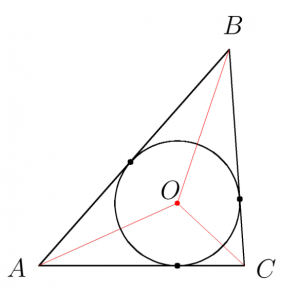 
Центр вписанной окружности
Центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Вписанный и описанный четырехугольники
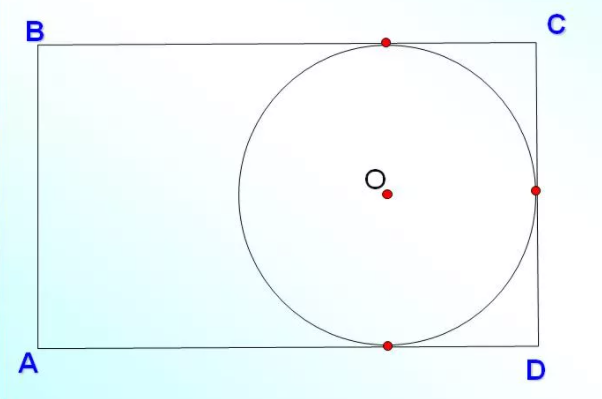
Не во всякий четырехугольник можно вписать окружность. Например, в прямоугольник нельзя вписать окружность. По рисунку видно, что окружность касается только трех его сторон, что не соответствует определению.
Условие вписанной в 4-х угольник окружности
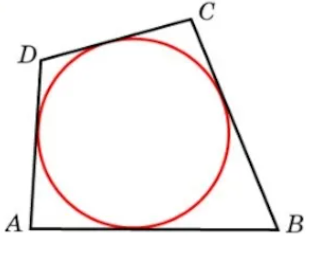
Окружность является вписанной в четырехугольник, если суммы длин противоположных сторон равны.
На рисунке выполняется данное условие, то есть AD + BC=DC + AB
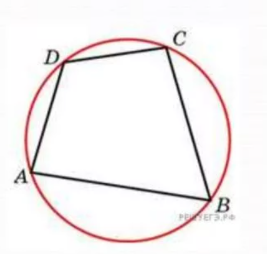
Окружность является описанной около четырехугольника, если суммы противоположных углов равны 180 градусов.
На рисунке окружности описана около четырехугольника, следовательно выполнено условие, что сумма углов А и С равна сумме углов B и D и равна 180 градусов.
Видео:Окружность, вписанная в правильный многоугольник. Видеоурок по геометрии 9 классСкачать
Окружность, вписанная в правильный многоугольник
На этом занятии мы рассмотрим следующую тему – «Окружность, вписанная в правильный многоугольник». В первую очередь дадим определение правильному многоугольнику. После чего докажем теорему о том, что внутри любого правильного многоугольника можно вписать окружность, и притом только одну. Кроме того, рассмотрим следствия из этой теоремы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
📸 Видео
Вписанная и описанная окружность - от bezbotvyСкачать
Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать
9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать
Окружность вписанная в треугольник и описанная около треугольника.Скачать
Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать
Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать
Вписанная и описанная окружности | Лайфхак для запоминанияСкачать
112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать
ТЕСТ НА ЭРУДИЦИЮ и кругозор: МНОГО УМНЫХ ВОПРОСОВ, ответы знает не каждый. #насколькотыумный #тестСкачать
Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать
Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать
Построить описанную окружность (Задача 1)Скачать
