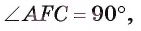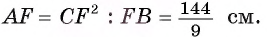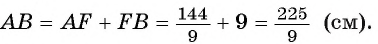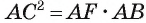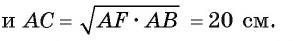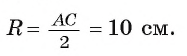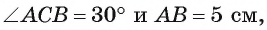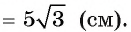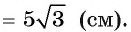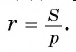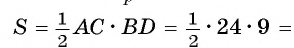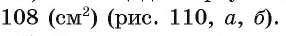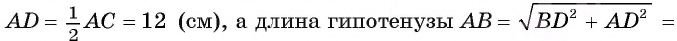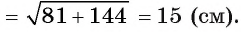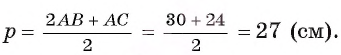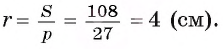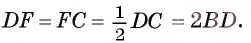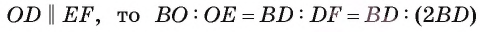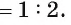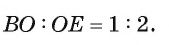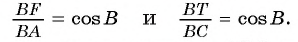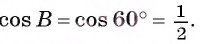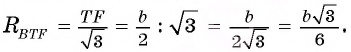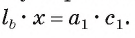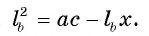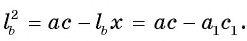Задачи треугольник с вписанной окружностью решения (8 видео)

Окружность вписана в треугольник

Окружность вписана в треугольник. В данной статье собрал для вас задачи, в которых даётся треугольник с вписанной в него или описанной около него окружностью. В условии ставится вопрос о нахождении радиуса окружности или стороны треугольника.

Данные задания удобно решать используя представленные формулы. Рекомендую их выучить, бывают очень полезны не только при решении этого типа заданий. Одна формула выражает связь радиуса вписанной в треугольник окружности с его сторонами и площадью, другая радиус описанной около треугольника окружности также с его сторонами и площадью:

где a, b, c – стороны треугольника

S – площадь треугольника

27900. Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120 0 . Найдите диаметр описанной окружности этого треугольника.

Здесь окружность описана около треугольника.

Диаметр мы сможем найти, если будет известен радиус. Используем формулу радиуса описанной около треугольника окружности:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны нам известны (боковые стороны равнобедренного треугольника), третью мы можем вычислить используя теорему косинусов:

Теперь вычислим площадь треугольника:

*Использовали формулу (2) из этой статьи .

Таким образом диаметр будет равен 2.

Это устные вычисления. Для тех кто имеет навык решения заданий с вписанным в окружность шестиугольником, тот сразу определит, что стороны треугольника АС и ВС «совпадают» со сторонами вписанного в окружность шестиугольника (угол шестиугольника как раз равен 120 0 , как и в условии задачи). А далее на основании того, что сторона вписанного в окружность шестиугольника равна радиусу этой окружности не сложно сделать вывод о том, что диаметр будет равен 2АС, то есть двум.

Подробнее о шестиугольнике посмотрите информацию в этой статье (п.5).

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:

А площадь треугольника будет равна 0,5х 2 .

Таким образом, гипотенуза будет равна:

В ответе требуется записать:

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.

По теореме Пифагора:

Воспользуемся формулой радиуса окружности вписанной в треугольник:

где a, b, c – стороны треугольника

S – площадь треугольника

Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:

27624. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

27625. Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.

27626. Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.

27923. Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.

27932. Катеты равнобедренного прямоугольного треугольника равны . Найдите радиус окружности, вписанной в этот треугольник.

Если в условии дан треугольник и вписанная или описанная окружность, и речь идёт о сторонах, площади, радиусе, то сразу вспомните об указанных формулах и пробуйте использовать их при решении. Если не получается, то тогда уже ищите другие способы решения.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Треугольники и окружность — задачи с примерами решения

Пример:

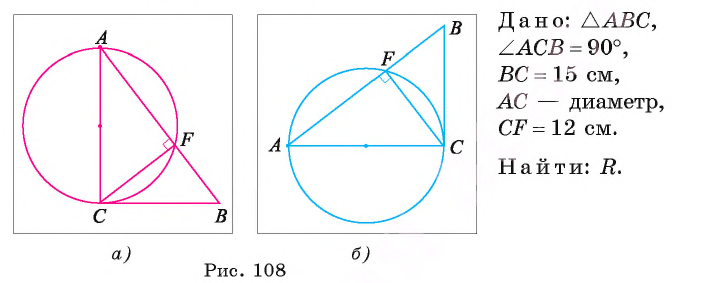
Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.

Решение:

Из условия следует, что радиус R равен половине катета АС. Заметим, что

1) В треугольнике

2) Воспользовавшись равенством 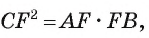найдем

3) Теперь

4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно,

Таким образом,

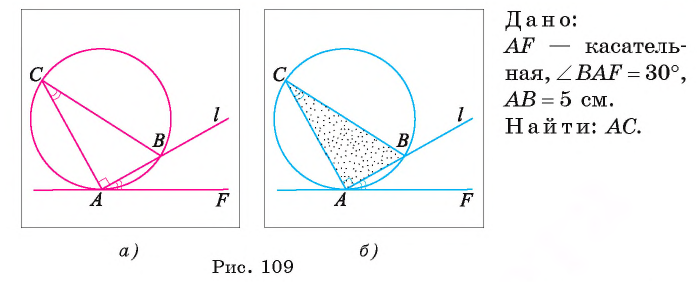
Пример:

Решение:

По теореме об угле между хордой и касательной 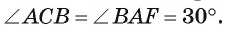Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как

Ответ

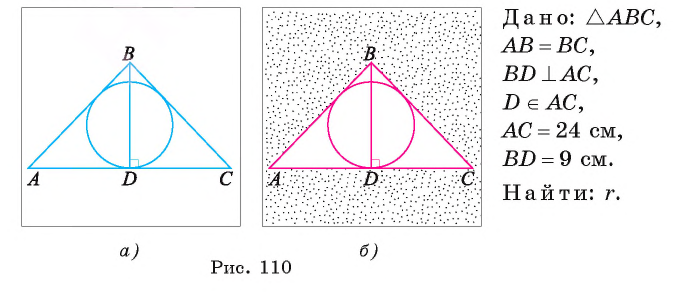
Пример:

Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.

Решение:

Для вычисления радиуса г вписанной окружности воспользуемся формулой 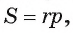где S — площадь треугольника, р — его полупериметр. Отсюда получим

1) Площадь треугольника

2) В прямоугольном треугольнике ADB длина катета

3) Теперь полупериметр

4) Таким образом, найдем

Пример:

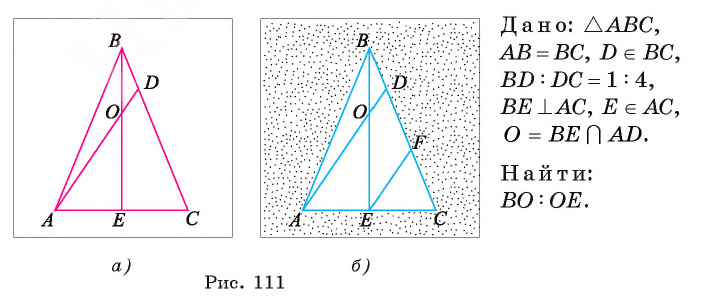
В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что 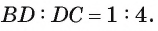В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?

Решение:

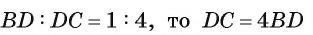
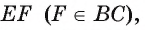
1) Так как (рис. 111, а, б). Проведем отрезок , параллельный отрезку AD.

2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.

3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,

4) Так как

Ответ:

Пример:

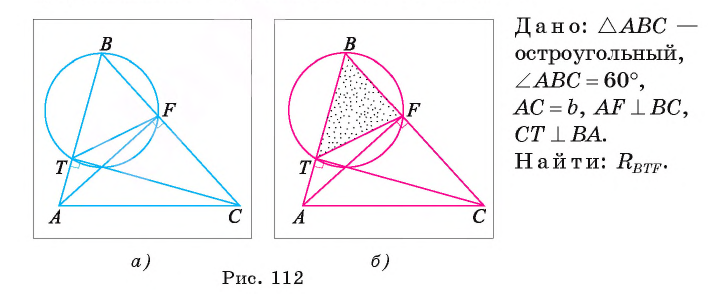
Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.

Решение:

Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.

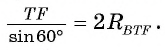
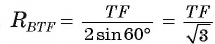
1) В треугольнике BTF по теореме синусов выполняется равенствоСледовательно, (рис. 112, a, 6).

2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно,

Следовательно,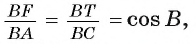т.е. треугольники подобны с коэффициентом подобия

3) Из подобия треугольников ABC и FTC следует, что 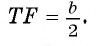Таким образом,

Ответ:

Пример:

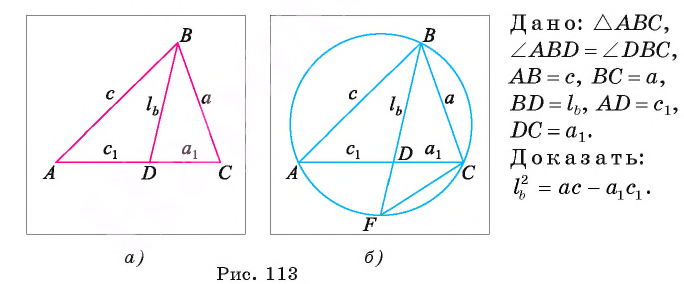
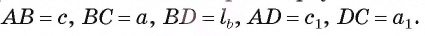
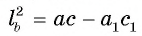
Отрезок BD — биссектриса треугольника ABC. Известно, что Докажите, что (рис. 113, а).

Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).

1) По свойству отрезков пересекающихся хорд выполняется равенство

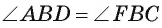
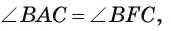
2) Треугольники ABD и FBC подобны, так как по условию и поскольку являются вписанными в окружность и опираются на одну и ту же дугу.

3) Из подобия треугольников ABD и FBC следует, что 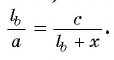Отсюда

3) Таким образом,

Что и требовалось доказать.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Площадь треугольника
Соотношения между сторонами и углами произвольного треугольника
Окружность и круг
Описанные и вписанные окружности
Пространственные фигуры — виды, изображения, свойства
Взаимное расположения прямых на плоскости
Треугольник
Решение треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Классификация задач на вписанные в треугольник и описанные около треугольника окружности

Разделы: Математика

Задачи на вписанные в треугольник и описанные около треугольника окружности вызывают даже у сильных учащихся затруднения при их решении. Попытка провести классификацию этих задач по содержанию и методам решения привела к положительным результатам. Учащиеся полюбили этот тип задач. Хотим поделиться нашим опытом.

Замечательное открытие: люди изобрели колесо.
Окружность, описанная около треугольника.
Окружность, вписанная в треугольник.
Задачи на вписанные и описанные окружности.

На востоке от Аравийского полуострова с севера на юг текут две большие реки – Евфрат и Тигр. Между ними тянется узкая длинная полоса земли. В древности она называлась Месопотамией, что в переводе означает “ Междуречье’’. Самым известным государством Месопотамии был Вавилон. Земля в Междуречье плодородная, но там не было ни металлов, ни камня, ни леса, чтобы строить дома. Всё это вавилонянам приходилось покупать у других народов. Поэтому Вавилон раньше других стран стал вести большую торговлю. Торговля помогала науке. В математике вавилонские учёные добились больших успехов.

Около шести тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо. Колесо? Что же тут замечательного? Но так кажется только на первый взгляд. Представьте себе на секунду, что вдруг случилось чудо, и на земле исчезли все колёса. Это было бы настоящей катастрофой! Остановятся автомобили и поезда, замрут заводы и фабрики, перестанут давать ток электростанции. Выходит, что неизвестный вавилонский изобретатель первого колеса действительно сделал великое открытие.

Вавилонские инженеры и мастера стали пользоваться блоками. Они поднимали и перетаскивали такие тяжести, справиться с которыми без колеса было бы не под силу. Колесо и рычаг стали первыми настоящими помощниками человека в работе с большими тяжестями.Так изобретение колеса сыграло очень большую роль в истории Вавилона.

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат в окружности.

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. Около любого треугольника можно описать окружность.

Доказательство: Рассмотрим произвольный В треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=ОВ=ОС. Поэтому окружность с центром О радиуса ОА проходит через О все три вершины треугольника и, значит, является описанной около треугольника АВС.

Вывод: Центр описанной около треугольника окружности лежит А С на пересечении серединных перпендикуляров и расположен:

а) в треугольнике, если он остроугольный;

б) на середине гипотенузы, если он прямоугольный;

в) вне треугольника, если он тупоугольный.

Рассмотрим задачи на нахождение радиуса описанной около треугольника окружности. (См. Приложение1.)

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. В любой треугольник можно вписать окружность.

Доказательство: Рассмотрим произвольный треугольник АВС и обозначим М буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры А К В ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА.

Так как точка О равноудалена A k B от сторон треугольника АВС то ОК = ОL=ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М.

Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ.

Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС.

Выводы. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника. Касательная к окружности (стороны треугольника) перпендикулярна к радиусу, проведённому в точку касания.

Рассмотрим задачи на нахождение радиуса вписанной в треугольник окружности.

Задачи на вписанную и описанную окружность. (См. Приложение 3.)