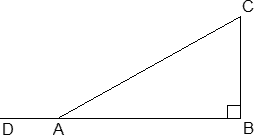Задачи по тригонометрии треугольника

Сегодня рассмотрим задачи B8 c тригонометрией в ее классическом понимании, где изучаются обычные прямоугольные треугольники. Поэтому никаких тригонометрических окружностей и отрицательных углов сегодня не будет — только обычные синусы и косинусы.

Такие задачи составляют примерно 30% от общего числа. Помните: если в задаче B8 хоть раз упоминается угол π , она решается совсем другими способами. Мы обязательно рассмотрим их в ближайшее время. А сейчас — главное определение урока:

— фигура на плоскости, состоящая из трех точек и отрезков, которые их соединяют. Фактически, это замкнутая ломаная из трех звеньев. Точки называются , а отрезки — сторонами. Важно заметить, что вершины не должны лежать на одной прямой, иначе треугольник вырождается в отрезок.

Довольно часто треугольником называют не только саму ломаную, но и часть плоскости, которая этой ломаной ограничена. Таким образом, можно определить площадь треугольника.

Два треугольника называются равными, если один можно получить из другого путем одного или нескольких движений плоскости: сдвига, поворота или симметрии. Кроме того, существует понятие подобных треугольников: их углы равны, а соответствующие стороны пропорциональны.

Все, что написано выше, можно было не читать. Потому что это не нужно. Вы что, не знаете, что такое треугольник? Вы действительно не знаете, как он выглядит? Хорошо, я сейчас покажу.

Это треугольник ABC . Более того, это прямоугольный треугольник: в нем ∠ C = 90°. Именно такие чаще всего и встречаются в задаче B8.

Все, что надо знать для решения задачи B8 — это несколько простых фактов из геометрии и тригонометрии, а также общая схема решения, в которой эти факты используются. Затем останется просто «набить руку».

Начнем с фактов. Они разбиты на три группы:

1. Определения и следствия из них;
2. Основные тождества;
3. Симметрии в треугольнике.

Нельзя сказать, что какая-то из этих групп важнее, сложнее или проще. Но информация, которая в них содержится, позволяет решить любую задачу B8. Поэтому знать надо все. Итак, поехали!

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Группа 1: определения и следствия из них

Рассмотрим треугольник ABC , где ∠ C — прямой. Для начала — определения:

угла — это отношение противолежащего катета к гипотенузе.

угла — это отношение прилежащего катета к гипотенузе.

угла — это отношение противолежащего катета к прилежащему.

Один угол или отрезок может входить в разные прямоугольные треугольники. Более того, очень часто один и тот же отрезок является катетом в одном треугольнике и гипотенузой — в другом. Но об этом — дальше, а пока будем работать с обычным углом А . Тогда:

Основные следствия из определения:

1. sin A = cos B ; cos A = sin B — самые часто используемые следствия
2. tg A = sin A : cos A — связывает тангенс, синус и косинус одного угла
3. Если ∠ A + ∠ B = 180°, т.е. углы смежные, то: sin A = sin B ; cos A = −cos B .

Хотите — верьте, хотите — нет, но этих фактов достаточно, чтобы решить примерно треть всех тригонометрических задач B8.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Группа 2: основные тождества

Первое и самое главное тождество — : квадрат гипотенузы равен сумме квадратов катетов. Применительно к треугольнику ABC , рассмотренному выше, эту теорему можно записать так:

AC 2 + BC 2 = AB 2

И сразу — небольшое замечание, которое убережет читателя от множества ошибок. Когда решаете задачу, всегда (слышите, всегда!) записывайте теорему Пифагора именно в таком виде. Не пытайтесь сразу выражать катет, как это обычно требуется. Возможно, вы сэкономите пару строчек вычислений, но именно на этой «экономии» было потеряно больше баллов, чем где-либо еще в геометрии.

Второе тождество — из тригонометрии. Выглядит следующим образом:

sin 2 A + cos 2 A = 1

Оно так и называется: . С его помощью можно через синус выразить косинус и наоборот.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Группа 3: Симметрии в треугольнике

То, что написано ниже, относится только к равнобедренным треугольникам. Если в задаче таковой не фигурирует, то для решения достаточно фактов из первых двух групп.

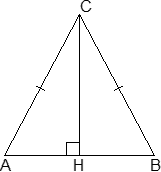
Итак, рассмотрим равнобедренный треугольник ABC , где AC = BC . Проведем к основанию высоту CH . Получим следующие факты:

1. ∠ A = ∠ B . Как следствие, sin A = sin B ; cos A = cos B ; tg A = tg B .
2. CH — не только высота, но и биссектриса, т.е. ∠ ACH = ∠ BCH . Аналогично, равны и тригонометрические функции этих углов.
3. Также CH — это медиана, поэтому AH = BH = 0,5 · AB .

Теперь, когда все факты рассмотрены, перейдем непосредственно к методам решения.

Видео:12 часов Тригонометрии с 0.Скачать

Общая схема решения задачи B8

Геометрия отличается от алгебры тем, что в ней нет простых и универсальных алгоритмов. Каждую задачу приходится решать с нуля — и в этом ее сложность. Тем не менее, общие рекомендации дать все-таки можно.

Для начала, следует обозначить неизвестную сторону (если таковая имеется) за X . Затем применяем схему решения, которая состоит из трех пунктов:

1. Если в задаче есть равнобедренный треугольник, применить к нему все возможные факты из третьей группы. Найдите равные углы и выразите их тригонометрические функции. Кроме того, равнобедренный треугольник редко бывает прямоугольным. Поэтому ищите в задаче прямоугольные треугольники — они там обязательно есть.
2. Применить к прямоугольному треугольнику факты из первой группы. Конечная цель — получить уравнение относительно переменной X . Найдем X — решим задачу.
3. Если фактов из первой группы оказалось недостаточно, применяем факты из второй группы. И снова ищем X .

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Примеры решения задач

А теперь попробуем с помощью полученных знаний решить наиболее распространенные задачи B8. Не удивляйтесь, что с таким арсеналом текст решения окажется не намного длиннее, чем исходное условие. И это радует 🙂

Задача. В треугольнике ABC угол C равен 90°, AB = 5, BC = 3. Найдите cos A .

По определению (группа 1), cos A = AC : AB . Гипотенуза AB нам известна, а вот катет AC придется искать. Обозначим его AC = x .

Переходим к группе 2. Треугольник ABC — прямоугольный. По теореме Пифагора:

AC 2 + BC 2 = AB 2 ;
x 2 + 3 2 = 5 2 ;
x 2 = 25 − 9 = 16;
x = 4.

Теперь можно найти косинус:

cos A = AC : AB = 4 : 5 = 0,8.

Задача. В треугольнике ABC угол B равен 90°, cos A = 4/5, BC = 3. BH — высота. Найдите AH .

Обозначим искомую сторону AH = x и рассмотрим треугольник ABH . Он прямоугольный, причем ∠ AHB = 90° по условию. Поэтому cos A = AH : AB = x : AB = 4/5. Это пропорция, ее можно переписать так: 5 · x = 4 · AB . Очевидно, мы найдем x , если будем знать AB .

Рассмотрим треугольник ABC . Он также прямоугольный, причем cos A = AB : AC . Ни AB , ни AC нам не известны, поэтому переходим ко второй группе фактов. Запишем основное тригонометрическое тождество:

sin 2 A + cos 2 A = 1;
sin 2 A = 1 − cos 2 A = 1 − (4/5) 2 = 1 − 16/25 = 9/25.

Поскольку тригонометрические функции острого угла положительны, получаем sin A = 3/5. С другой стороны, sin A = BC : AC = 3 : AC . Получаем пропорцию:

3 : AC = 3 : 5;
3 · AC = 3 · 5;
AC = 5.

Итак, AC = 5. Тогда AB = AC · cos A = 5 · 4/5 = 4. Наконец, находим AH = x :

5 · x = 4 · 4;
x = 16/5 = 3,2.

Задача. В треугольнике ABC AB = BC , AC = 5, cos C = 0,8. Найдите высоту CH .

Обозначим искомую высоту CH = x . Перед нами равнобедренный треугольник ABC , в котором AB = BC . Следовательно, из третьей группы фактов имеем:

∠ A = ∠ C ⇒ cos A = cos C = 0,8

Рассмотрим треугольник ACH . Он прямоугольный (∠ H = 90°), причем AC = 5 и cos A = 0,8. По определению, cos A = AH : AC = AH : 5. Получаем пропорцию:

AH : 5 = 8 : 10;
10 · AH = 5 · 8;
AH = 40 : 10 = 4.

Осталось воспользоваться второй группой фактов, а именно теоремой Пифагора для треугольника ACH :

AH 2 + CH 2 = AC 2 ;
4 2 + x 2 = 5 2 ;
x 2 = 25 − 16 = 9;
x = 3.

Задача. В прямоугольном треугольнике ABC ∠ B = 90°, AB = 32, AC = 40. Найдите синус угла CAD .

Поскольку нам известна гипотенуза AC = 40 и катет AB = 32, можно найти косинус угла A : cos A = AB : AC = 32 : 40 = 0,8. Это был факт из первой группы.

Зная косинус, можно найти синус через основное тригонометрическое тождество (факт из второй группы):

sin 2 A + cos 2 A = 1;
sin 2 A = 1 − cos 2 A = 1 − 0,8 2 = 0,36;
sin A = 0,6.

При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы BAC и CAD смежные. Из первой группы фактов имеем:

∠ BAC + ∠ CAD = 180°;
sin CAD = sin BAC = sin A = 0,6.

Задача. В треугольнике ABC AC = BC = 5, AB = 8, CH — высота. Найдите tg A .

Треугольник ABC — равнобедренный, CH — высота, поэтому заметим, что AH = BH = 0,5 · AB = 0,5 · 8 = 4. Это факт из третьей группы.

Теперь рассмотрим треугольник ACH : в нем ∠ AHC = 90°. Можно выразить тангенс: tg A = CH : AH . Но AH = 4, поэтому остается найти сторону CH , которую обозначим CH = x . По теореме Пифагора (факт из группы 2) имеем:

AH 2 + CH 2 = AC 2 ;
4 2 + x 2 = 5 2 ;
x 2 = 25 − 16 = 9;
x = 3.

Теперь все готово, чтобы найти тангенс: tg A = CH : AH = 3 : 4 = 0,75.

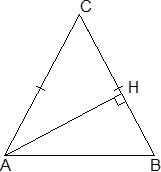
Задача. В треугольнике ABC AC = BC , AB = 6, cos A = 3/5. Найдите высоту AH .

Обозначим искомую высоту AH = x . Снова треугольник ABC — равнобедренный, поэтому заметим, что ∠ A = ∠ B , следовательно, cos B = cos A = 3/5. Это факт из третьей группы.

Рассмотрим треугольник ABH . По условию, он прямоугольный (∠ AHB = 90°), причем известна гипотенуза AB = 6 и cos B = 3/5. Но cos B = BH : AB = BH : 6 = 3/5. Получили пропорцию:

BH : 6 = 3 : 5;
5 · BH = 6 · 3;
BH = 18/5 = 3,6.

Теперь найдем AH = x по теореме Пифагора для треугольника ABH :

AH 2 + BH 2 = AB 2 ;
x 2 + 3,6 2 = 6 2 ;
x 2 = 36 − 12,96 = 23,04;
x = 4,8.

Видео:Решение задачи с применением теоремы синусовСкачать

Дополнительные соображения

Бывают нестандартные задачи, где рассмотренные выше факты и схемы бесполезны. Увы, в таком случае нужен действительно индивидуальный подход. Подобные задачи любят давать на всевозможных «пробных» и «демонстрационных» экзаменах.

Ниже приведены две реальные задачи, которые предлагались на пробном ЕГЭ в Москве. Справились с ними единицы, что свидетельствует о высокой сложности этих задач.

Задача. В прямоугольном треугольнике ABC из угла C = 90° провели медиану и высоту. Известно, что ∠ A = 23°. Найдите ∠ MCH .

Заметим, что медиана CM проведена к гипотенузе AB , поэтому M — центр описанной окружности, т.е. AM = BM = CM = R , где R — радиус описанной окружности. Следовательно, треугольник ACM — равнобедренный, и ∠ ACM = ∠ CAM = 23°.

Теперь рассмотрим треугольники ABC и CBH . По условию, оба треугольника прямоугольные. Кроме того, ∠ B — общий. Следовательно, треугольники ABC и CBH подобны по двум углам.

В подобных треугольника соответствующие элементы пропорциональны. В частности:

Наконец, рассмотрим ∠ C . Он прямой, и, кроме того, ∠ C = ∠ ACM + ∠ MCH + ∠ BCH . В этом равенстве ∠ MCH — искомый, а ∠ ACM и ∠ BCH известны и равны 23°. Имеем:

90° = 23° + MCH + 23°;
MCH = 90° − 23° − 23° = 44°.

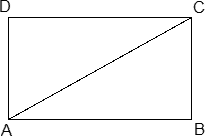
Задача. Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Обозначим стороны прямоугольника: AB = x , BC = y . Выразим периметр:

P_ABCD = 2 · ( AB + BC ) = 2 · ( x + y ) = 34;
x + y = 17.

Аналогично выразим площадь: S_ABCD = AB · BC = x · y = 60.

Теперь рассмотрим треугольник ABC . Он прямоугольный, поэтому запишем теорему Пифагора:

AB 2 + BC 2 = AC 2 ;
AC 2 = x 2 + y 2 .

Заметим, что из формулы квадрата разности следует равенство:

x 2 + y 2 = ( x + y ) 2 − 2 · x · y = 17 2 − 2 · 60 = 289 − 120 = 169

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Видео:Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Видео:Супер ЖЕСТЬ ➜ Найдите сторону треугольника ➜ Решить без тригонометрииСкачать

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Видео:Профильный ЕГЭ 2023. Задача 3. Тригонометрия треугольника. 10 класс.Скачать

Тригонометрия: Таблица значений тригонометрических функций

0 °30 °45 °60 °90 °sin α01 22 23 21cos α13 22 21 20tg α03 313нетctg αнет313 30

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Видео:8 класс, 29 урок, Синус, косинус и тангенс острого угла прямоугольного треугольникаСкачать

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Видео:ТРИГОНОМЕТРИЯ с нуля — Синус, косинус, тангенс и котангенс острого углаСкачать

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Видео:ТРИГОНОМЕТРИЯ с нуля за 30 минутСкачать

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Видео:Геометрия 8 класс : Решение задач на sin, cos и tg острого угла прямоугольного треугольникаСкачать

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Видео:Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Видео:Тригонометрия: Как запомнить? + ПОЛУЧИ ПОДАРОК от Ольги АлександровныСкачать

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

Видео:Решение задач. Синус косинус тангенс котангенс 8 классСкачать

Материал для проведения зачета на тему» Прямоугольный треугольник. Решение задач с использованием определения тригонометрических функций»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ зачет на тему использование тригонометрических функций.docx

Зачет на тему «Решение задач с использованием определения тригонометрических функций »

В треугольнике ABC угол C равен 90°, ВС=25 , Найдите AC .

В треугольнике ABC угол C равен 90°, ВС =2. , Найдите АС .

В треугольнике ABC угол C равен 90°, АВ=13 , Найдите высоту CH .

В треугольнике АВС угол С равен 90°,АС=4 , Найдите АВ.

В треугольнике АВС угол С равен 90°, , АС=4 . Найдите АВ.

В треугольнике ABC угол C равен 90°, ВС =3. Найдите АВ .

В треугольнике ABC угол C равен 90°, ВС =3. Найдите АВ .

Выбранный для просмотра документ формулы.docx

Краткое описание документа:

В данном архиве представителен материал для проведения зачета в 9 классе, а также для подготовки к ОГЭ и ЕГЭ по математики для 9 и 11 классов. Тема зачета «Прямоугольный треугольник. Решение задач с использованием определения тригонометрических функций.» Архив состоит из: 1) файла со справочными материалами, 2) скан.версия решение задачи № 1 из зачет I способом, 3) скан.версия решение задачи № 1 из зачет II способом, 4) лист-зачет.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Основное тригонометрическое тождество. 8 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 555 229 материалов в базе

Материал подходит для УМК

«Геометрия. 7-9 класс», Волович М.Б., Атанасян Л.С.

Глава 9. Соотношение между сторонами и углами треугольника

Другие материалы

• 19.02.2018
• 1103
• 20

• 19.02.2018
• 483
• 0

• 19.02.2018
• 421
• 2

• 19.02.2018
• 226
• 0

• 19.02.2018
• 1363
• 1

• 19.02.2018
• 485
• 0

• 19.02.2018
• 1079
• 19

• 18.02.2018
• 8575
• 394

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 20.02.2018 2980
• RAR 2.2 мбайт
• 33 скачивания
• Оцените материал:

Настоящий материал опубликован пользователем Варелиди Ольга Андреевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 4 года
• Подписчики: 0
• Всего просмотров: 6571
• Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили ввести пост уполномоченного по правам учителей

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В России классы будут переводить на дистант, если заболели 20% детей

Время чтения: 1 минута

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

Новые курсы: управление детским садом, коучинг, немецкий язык и другие

Время чтения: 18 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.