Один из самых популярных методов дискретизации сферических областей основан на варианте метода дробления. Как и в случае с кругом, шар разбивается на сектора, но уже тетраэдрической формы. Для этого можно использовать либо 3 взаимно перпендикулярные плоскости, проходящие через центр шара (рис. 14), либо вписанный в шар икосаэдр (правильный 20-гранник, гранями которого являются равносторонние треугольники). Второй вариант предпочтительней из-за существенно меньших геометрических искажений сетки при ее построении (рис. 15).
Рис. 14. Разбиение сферы на 8 секторов
Рис. 15. Разбиение сферы на 20 секторов с помощью вписанного икосаэдра
Идея методов дробления состоит в последовательном измельчении некоторой уже построенной грубой сетки путем дробления ее элементов. В данном случае необходимо раздробить сектора, имеющие форму тетраэдров с одной кривой гранью. Особенностью этой задачи является то, что использование одинакового шаблона для каждого сектора автоматически обеспечивает согласование триангуляции между секторами ввиду очевидной симметрии.
Рассмотрим два возможных шаблона дробления тетраэдра.
Первый шаблон предполагает разбиение тетраэдра на 8 частей. Для этого каждое его ребро делится надвое дополнительным узлом; через эти узлы проводятся плоскости, отсекающие 4 тетраэдра с исходными вершинами. Оставшийся в итоге объемный ромб (если тетраэдр был правильный, то получится октаэдр) делится на 4 тетраэдра вставкой внутреннего ребра (из трех возможных вариантов проведения ребра выбирается оптимальный).
Рис. 16. Дробление тетраэдра на 8 частей
При использовании второго шаблона тетраэдр разбивается на 27 частей. Для этого необходимо разбить каждое его ребро на три равные части и вставить по дополнительному узлу в центр каждой грани. Каждая грань при этом разобьется на 9 треугольников. Соединив ребрами узлы, лежащие в центрах граней, получим разбиение исходного тетраэдра на 11 тетраэдров и 4 объемных ромба, каждый из которых затем оптимальным образом разбивается на 4 тетраэдра.
Рис. 17. Дробление тетраэдра на 27 частей
Процесс дробления можно продолжать итерационно до тех пор, пока элементы не станут нужного размера.
Единственная сложность, с которой можно столкнуться при использовании этого шаблона для дискретизации секторов, заключается в наличии «кривой» (выпуклой) грани. Однако этой сложности можно избежать, если использовать не декартовы, а сферические координаты. В этом случае нужные координаты новых узлов будут получаться автоматически, без использования каких-либо процедур отображения. Ниже приведена двумерная аналогия этого принципа.
Заметим, что при использовании метода дробления на основе 20 секторов сетка, которая образуется на границе сферы, будет состоять из правильных треугольников. Это весьма благотворно сказывается на качестве аппроксимации граничных условий [18]. Общее качество дискретизации шара методом дробления также довольно велико, хотя и (слабо экспоненциально) ухудшается с каждым шагом дробления. Для трех шагов дробления (при дроблении на 27 тетраэдров) средняя АХ будет около 0.5 (при этом линейные размеры элементов будут составлять примерно 1/50 от диаметра шара). К сожалению, сетки на основе метода дробления неоднородны и, как правило, не имеют четкой топологической структуры (при оптимальном подборе направления вставляемых ребер).
- Геодезический купол. Об устройстве и моем опыте расчетов
- Метод равных дуг.
- GIS-LAB
- Создание треугольных сеток на сфере
- Содержание
- [править] Постановка задачи
- [править] Генерация сетки в сферическом треугольнике
- [править] Метод бисекции
- [править] Метод трисекции
- [править] Программная реализация
- [править] Сферические многогранники
- 🎥 Видео
Видео:№584. Все стороны треугольника ABC касаются сферы радиуса 5 см. Найдите расстояние от центра сферыСкачать

Геодезический купол. Об устройстве и моем опыте расчетов
Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.
Википедию цитировать не буду. Почему я выбрал купол в качестве дома?
- При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
- Мне нравится как выглядит сфера.
- Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!
Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.
В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.
Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.
Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.
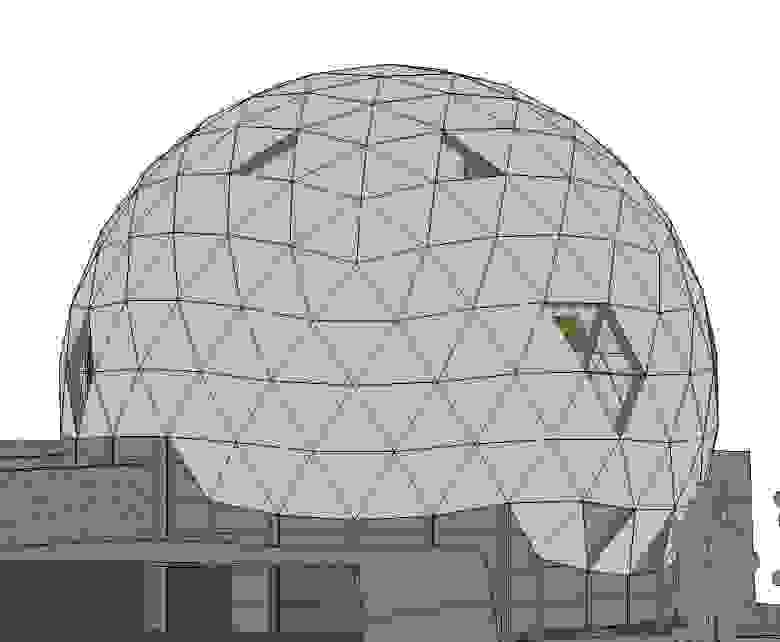
Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.
Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.
В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.
Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.
Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.
Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.
Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.
Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.
Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.
Метод равных дуг.
Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.
Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.
Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.
Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:
Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.
Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:
Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!
Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.
Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.
Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.
Конечно, трудности на этом не закончились, но это уже совсем другая история.
Видео:№581. Вершины треугольника ABC лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы доСкачать
GIS-LAB
Географические информационные системы и дистанционное зондирование
Видео:№583. Стороны треугольника касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскоСкачать

Создание треугольных сеток на сфере
Рассматриваются вопросы создания треугольной сетки на сфере. Приводится программа построения сетки в сферическом треугольнике на Си. Прилагаются слои сетки на основе икосаэдра.
Видео:🔥 ФОКУС с треугольником #shortsСкачать

Содержание
Видео:FreeCad Сфера из треугольниковСкачать

[править] Постановка задачи
Требуется создать регулярное покрытие сферы треугольниками, близкими по размеру и форме. В качестве эталона примем сетку, образованную на плоскости равносторонними треугольниками. Отличие геометрии треугольника от правильной равносторонней будем интерпретировать как искажение формы. [1]
В начале рассмотрим алгоритм построения сетки в базовом сферическом треугольнике. Затем уделим внимание различным способам разделения сферы на базовые сферические треугольники. Наконец, представим пример создания треугольной сетки на основе икосаэдра.
Видео:Геометрия Стороны треугольника касаются сферы радиуса 5 см. Определите расстояние от центра сферыСкачать

[править] Генерация сетки в сферическом треугольнике
Процедуру создания на некоторой поверхности сетки треугольников обычно называют триангуляцией. В качестве базы для создания сетки используем некоторый сферический треугольник, заданный координатами своих вершин.
[править] Метод бисекции
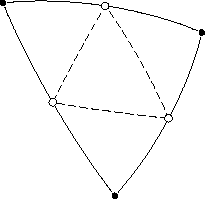
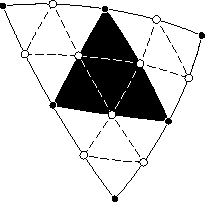
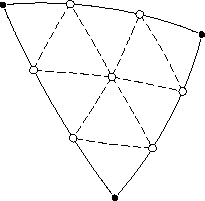
Назовём бисекцией операцию деления исходного треугольника на четыре треугольника нового поколения. Собственно термин «бисекция» относится к делению сторон пополам. В середины рёбер вставляются новые вершины (белые точки на рисунках), которые соединяются новыми рёбрами (пунктирные линии), образующими новые треугольники. Следующее поколение получается очередной бисекцией.
В терминах геометрии на сфере задача вставки точек в стороны треугольников решается последовательным решением обратной и прямой геодезических задач. Однако в данном случае гораздо проще использовать векторную алгебру. Пусть концы стороны заданы векторами a и b; тогда средняя точка f вычисляется как их нормированная сумма:







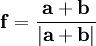
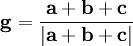











![Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]](https://i.ytimg.com/vi/JsrRqLK8zKg/0.jpg)
