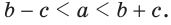Неравенство треугольника векторное доказательство

Содержание:

Неравенство треугольника:

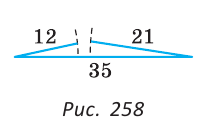
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

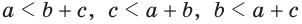
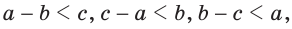
Замечание. Из неравенств треугольника следует, что то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо

Пример:

Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:

Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС B (рис. 108, а).

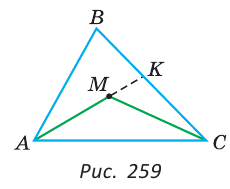
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF 1.

4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.

5) Так как треугольник FАС является равнобедренным, то 1 = 2.

Таким образом, BСА > 1, 1 = 2 и 2 > B.

Отсюда получаем, что ВСА > B.

Теорема 2. В треугольнике против большего угла лежит большая сторона.

1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.

В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.

Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.

Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.

Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.

Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.

Неравенство треугольника

Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.

Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Неравенства треугольника. 7 класс.Скачать

Неравенство треугольника векторное доказательство

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Евклидовы пространства Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

Глава 4
ЕВКЛИДОВЫ ПРОСТРАНСТВА

Из курса аналитической геометрии читатель знаком с понятием скалярного произведения двух свободных векторов и с четырьмя основными свойствами указанного скалярного произведения. В настоящей главе изучаются линейные пространства любой природы, для элементов которых каким-либо способом (причем безразлично каким) определено правило, ставящее в соответствие любым двум элементам число, называемое скалярным произведением этих элементов. При этом важно только, чтобы это правило обладало теми же четырьмя свойствами, что и правило составления скалярного произведения двух свободных векторов. Линейные пространства, в которых определено указанное правило, называются евклидовыми пространствами. В настоящей главе выясняются основные свойства произвольных евклидовых пространств.

§ 1. Вещественное евклидово пространство и его простейшие свойства

1. Определение вещественного евклидова пространства. Вещественное линейное пространство R называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования.
I. Имеется правило, посредством которого любым двум элементам этого пространства х и у ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом (х, у).
П. Указанное правило подчинено следующим четырем аксиомам:
1°. (х, у) = (у, х) (переместительное свойство или симметрия);
2°. (x₁ + x 2, у) = (х₁ , у) + (х₂, у) (распределительное свойство);
3°. ( λ х, у) = λ (х, у) для любого вещественного λ ;
4°. (х, х) > 0, если х — ненулевой элемент; (х, х) = 0, если х — нулевой элемент.
Подчеркнем, что при введении понятия евклидова пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов, произведения элемента на число и скалярного произведения элементов (важно лишь, чтобы эти правила удовлетворяли восьми аксиомам линейного пространства и четырем аксиомам скалярного произведения).
Если же природа изучаемых объектов и вид перечисленных правил указаны, то евклидово пространство называется конкретным.
Приведем примеры конкретных евклидовых пространств.
Пример 1. Рассмотрим линейное пространство В₃, всех свободных векторов. Скалярное произведение любых двух векторов определим так, как это было сделано в аналитической геометрии (т. е. как произведение длин этих векторов на косинус угла между ними). В курсе аналитической геометрии была доказана справедливость для так определенного скалярного произведения аксиом 1°- 4° (см. выпуск «Аналитическая геометрия», гл.2, §2, п.З). Стало быть, пространство В₃ с так определенным скалярным произведением является евклидовым пространством.
Пример 2. Рассмотрим бесконечномерное линейное пространство С [а, b ] всех функций x(t), определенных и непрерывных на сегменте а ≤ t ≤ b . Скалярное произведение двух таких функций x(t) и y(t) определим как интеграл (в пределах от а до b ) от произведения этих функций

Элементарно проверяется справедливость для так определенного скалярного произведения аксиом 1°-4°. В самом деле, справедливость аксиомы 1° очевидна; справедливость аксиом 2° и 3° вытекает из линейных свойств определенного интеграла; справедливость аксиомы 4° вытекает из того, что интеграл от непрерывной неотрицательной функции x 2 (t) неотрицателен и обращается в нуль лишь тогда, когда эта функция тождественно равна нулю на сегменте а ≤ t ≤ b (см. выпуск «Основы математического анализа», часть I, свойства 1° и 2° из п. 1 §6 гл. 10) (т.е. является нулевым элементом рассматриваемого пространства).
Таким образом, пространство С [а, b ] с так определенным скалярным произведением представляет собой бесконечномерное евклидово пространство.
Пример 3. Следующий пример евклидова пространства дает n-мерное линейное пространство А _n упорядоченных совокупностей n вещественных чисел, скалярное произведение двух любых элементов х= (х₁, x₂. х_n) и у = ( y ₁, y ₂. y _n) которого определяется равенством

Справедливость для так определенного скалярного произведения аксиомы 1° очевидна; справедливость аксиом 2° и 3° легко проверяется достаточно вспомнить определение операций сложения элементов и умножения их на числа:

наконец, справедливость аксиомы 4° вытекает из того, что (х, х) = х₁ 2 + x₂ 2 + . + х_n 2 всегда является неотрицательным числом и обращается в нуль лишь при условии х₁ = х₂ = . = х _n = 0.
Рассмотренное в этом примере евклидово пространство часто обозначают символом Е _n .
Пример 4. В том же самом линейном пространстве А _n введем скалярное произведение любых двух элементов х= (х₁, x₂. х_n) и у = ( y ₁, y ₂. y _n) не соотношением (4.2), а другим, более общим, способом.
Для этого рассмотрим квадратную матрицу порядка n

Составим с помощью матрицы (4.3) однородный многочлен второго порядка относительно n переменных х₁, x₂. х_n

Забегая вперед, отметим, что такой многочлен называется квадратичной формой (порождаемой матрицей (4.3)) ( квадратичные формы систематически изучаются в гл. 7 этой книги).
Квадратичная форма (4.4) называется положительно определенной, если она принимает строго положительные значения для всех значений переменных х₁, x₂. х_n , одновременно не равных нулю (в гл. 7 этой книги будет указано необходимое и достаточное условие положительной определенности квадратичной формы).
Так как при х₁ = х₂ = . = х _n = 0 квадратичная форма (4.4), очевидно, равна нулю, то можно сказать, что положительно определенная
квадратичная форма обращается в нуль лишь при условии х₁ = х₂ = . = х _n = 0.
Потребуем, чтобы матрица (4.3) удовлетворяла двум условиям.
1°. Порождала положительно определенную квадратичную форму (4.4).
2°. Была симметричной (относительно главной диагонали), т.е. удовлетворяла условию a_ik = а _ki для всех i = 1, 2. n и k = I, 2. n .
С помощью матрицы (4.3), удовлетворяющей условиям 1° и 2°, определим скалярное произведение двух любых элементов х= (х₁, x₂. х_n) и у = ( y ₁, y ₂. y _n) пространства А _n соотношением

Легко проверить справедливость для так определенного скалярного произведения всех аксиом 1°-4°. В самом деле, аксиомы 2° и 3°, очевидно, справедливы при совершенно произвольной матрице (4.3); справедливость аксиомы 1° вытекает из условия симметричности матрицы (4.3), а справедливость аксиомы 4° вытекает из того, что квадратичная форма (4.4), представляющая собой скалярное произведение (х, х), является положительно определенной.
Таким образом, пространство А _n со скалярным произведением, определяемым равенством (4.5), при условии симметричности матрицы (4.3) и положительной определенности порождаемой ею квадратичной формы, является евклидовым пространством.
Если в качестве матрицы (4.3) взять единичную матрицу, то соотношение (4.4) перейдет в (4.2), и мы получим евклидово пространство Е _n , рассмотренное в примере 3.
2. Простейшие свойства произвольного евклидова пространства. Устанавливаемые в этом пункте свойства справедливы для совершенно произвольного евклидова пространства как конечной, так и бесконечной размерности.
Теорема 4.1. Для любых двух элементов х и у произвольного евклидова пространства справедливо неравенство

( x, y ) 2 ≤ ( x, x )( y, y ), (4.6)

называемое неравенством Коши-Буняковского.
Доказательство. Для любого вещественного числа λ , в силу аксиомы 4° скалярного произведения, справедливо неравенство ( λ х — у, λ х — у) > 0. В силу аксиом 1°-3°, последнее неравенство можно переписать в виде

λ 2 (x, x) — 2 λ (x, y) + (y, y) ≤ 0

Необходимым и достаточным условием неотрицательности последнего квадратного трехчлена является неположительность его дискриминанта, т. е. неравенство (в случае (х, х) = 0 квадратный трехчлен вырождается в линейную функцию, но в этом случае элемент х является нулевым, так что (х, у) = 0 и неравенство (4.7) также справедливо)

( x, y ) 2 — ( x, x )( y, y ) ≤ 0. (4.7)

Из (4.7) сразу же вытекает неравенство (4.6). Теорема доказана.
Наша очередная задача — ввести в произвольном евклидовом пространстве понятие нормы (или длины) каждого элемента. Для этого введем понятие линейного нормированного пространства.
Определение. Линейное пространство R называется нормированным, если выполнены следующие два требования.
I. Имеется правило, посредством которого каждому элементу х пространства R ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом ||х||.
П. Указанное правило подчинено следующим трем аксиомам:
1°. ||х|| > 0, если х — ненулевой элемент; ||х|| = 0, если х — нулевой элемент;
2°. || λ х|| = | λ | ||х|| для любого элемента х и любого вещественного числа λ ;
3°. для любых двух элементов х и у справедливо следующее неравенство

называемое неравенством треугольника (или неравенством Минковского).
Теорема 4.2. Всякое евклидово пространство является нормированным, если норму любого элемента х в нем определить равенством

Доказательство. Достаточно доказать, что для нормы, определенной соотношением (4.9), справедливы аксиомы 1°-3° из определения нормированного пространства.
Справедливость для нормы аксиомы 1° сразу вытекает из аксиомы 4° скалярного произведения. Справедливость для нормы аксиомы 2° почти непосредственно вытекает из аксиом 1° и 3° скалярного произведения.
Остается убедиться в справедливости для нормы аксиомы 3°, т. е. неравенства (4.8). Будем опираться на неравенство Коши-Буняковского (4.6), которое перепишем в виде

С помощью последнего неравенства, аксиом 1°-4° скалярного произведения и определения нормы получим

Теорема доказана.
Следствие. Во всяком евклидовом пространстве с нормой элементов, определяемой соотношением (4.9), для любых двух элементов х и у справедливо неравенство треугольника (4.8).

Заметим далее, что в любом вещественном евклидовом пространстве можно ввести понятие угла между двумя произвольными элементами х и у этого пространства. В полной аналогии с векторной алгеброй, мы назовем углом φ между элементами х и у тот (изменяющийся в пределах от 0 до π ) угол, косинус которого определяется соотношением

Данное нами определение угла корректно, ибо в силу неравенства Коши-Буняковского (4.7′) дробь, стоящая в правой части последнего равенства, по модулю не превосходит единицы.
Далее договоримся называть два произвольных элемента х и у евклидова пространства Е ортогональными, если скалярное произведение этих элементов (х, у) равно нулю (в этом случае косинус угла ( φ между элементами х и у будет равен нулю).
Снова апеллируя к векторной алгебре, назовем сумму х + у двух ортогональных элементов х и у гипотенузой прямоугольного треугольника, построенного на элементах х и у.
Заметим, что во всяком евклидовом пространстве справедлива теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. В самом деле, поскольку х и у ортогональны и (х, у) = 0, то в силу аксиом и определения нормы

||х + y || 2 = ( x+y, x+y ) = ( x, x ) + 2( x, y ) + (y, y) = (x,x) + (y, y) = ||х|| 2 + || y || 2 .

Этот результат обобщается и на n попарно ортогональных элементов х₁, x₂. х_n: если z = х₁ + x₂ + . + х_n, то

В заключение запишем норму, неравенство Коши-Буняковского и неравенство треугольника в каждом из конкретных евклидовых пространств, рассмотренных в предыдущем пункте.
В евклидовом пространстве всех свободных векторов с обычным определением скалярного произведения норма вектора а совпадает с его длиной |а|, неравенство Коши-Буняковского приводится к виду (( a,b ) 2 ≤ |а| 2 | b | 2 , а неравенство треугольника — к виду |a + b| ≤ |а| + | b | (Если сложить векторы а и b по правилу треугольника, то это неравенство тривиально сводится к тому, что одна сторона треугольника не превосходит суммы двух других его сторон).
В евклидовом пространстве С [а, b ] всех непрерывных на сегменте а ≤ t ≤ b функций х = x(t) со скалярным произведением (4.1) норма элемента х = x(t) равна , а неравенства Коши-Буняковского и треугольника имеют вид

Оба эти неравенства играют важную роль в различных разделах математического анализа.
В евклидовом пространстве Е _n упорядоченных совокупностей n вещественных чисел со скалярным произведением (4.2) норма любого элемента х = (х₁, x₂. х_n) равна

а неравенства Коши-Буняковского и треугольника имеют вид

Наконец, в евклидовом пространстве упорядоченных совокупностей n вещественных чисел со скалярным произведением (4.5) норма любого элемента х = (х₁, x₂. х_n) равна 0 (напоминаем, что при этом матрица (4.3) симметрична и порождает положительно определенную квадратичную форму (4.4)).

а неравенства Коши-Буняковского и треугольника имеют вид

Видео:✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать

Неравенство треугольника: доказательство, примеры, решенные упражнения

Неравенство треугольника: доказательство, примеры, решенные упражнения — Наука

Видео:Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать

Содержание:

Это называется неравенство треугольника к свойству двух действительных чисел, заключающемуся в том, что абсолютное значение их суммы всегда меньше или равно сумме их абсолютных значений. Это свойство также известно как неравенство Минковского или треугольное неравенство.

Это свойство чисел называется треугольным неравенством, потому что в треугольниках длина одной стороны всегда меньше или равна сумме двух других, даже если это неравенство не всегда применяется в области треугольников.

Существует несколько доказательств треугольного неравенства в действительных числах, но в этом случае мы выберем одно, основанное на свойствах абсолютного значения и биномиального квадрата.

Теорема: Для каждой пары чисел к Y б относящиеся к действительным числам, он должен:

Видео:Неравенство треугольникаСкачать

Демонстрация

Начнем с рассмотрения первого члена неравенства, который возведем в квадрат:

| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (уравнение 1)

На предыдущем шаге мы использовали свойство, согласно которому любое число в квадрате равно абсолютному значению указанного числа в квадрате, то есть:| х | ^ 2 = х ^ 2. Также использовалось квадратное биномиальное разложение.

Все номера Икс меньше или равно его абсолютному значению. Если число положительное, оно равно, но если число отрицательное, оно всегда будет меньше положительного числа. В этом случае его собственное абсолютное значение, то есть можно сказать, что x ≤ | х |.

Продукт (а б) является числом, поэтому применяется, что (а б) ≤ | а б |. Когда это свойство применяется к (уравнение 1), мы имеем:

| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | а б | + b ^ 2 (уравнение 2)

Учитывая, что | a b | = | а || б | la (уравнение 2) можно записать следующим образом:

| a + b | ^ 2 ≤ a ^ 2 + 2 | а || б | + b ^ 2 (уравнение 3)

Но поскольку мы говорили ранее, что квадрат числа равен абсолютному значению квадрата числа, то уравнение 3 можно переписать следующим образом:

| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | б | + | b | ^ 2 (уравнение 4)

Во втором члене неравенства признается замечательный продукт, применение которого приводит к:

| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (уравнение 5)

В предыдущем выражении следует отметить, что значения, которые должны быть возведены в квадрат в обоих членах неравенства, положительны, поэтому необходимо также убедиться, что:

| а + б | ≤ (| a | + | b |) (уравнение 6)

Вышеприведенное выражениеэто именно то, что хотели продемонстрировать.

Видео:Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать

Примеры

Далее мы проверим треугольное неравенство на нескольких примерах.

Видео:Неравенство треугольникаСкачать

Пример 1

Мы берем значение a = 2 и значение b = 5, то есть оба положительных числа, и проверяем, выполняется ли неравенство.

Равенство проверено, следовательно, теорема о неравенстве треугольника выполнена.

Видео:7 класс, 34 урок, Неравенство треугольникаСкачать

Пример 2

Выбираются следующие значения a = 2 и b = -5, то есть положительное число, а другое отрицательное, проверяем, выполняется неравенство или нет.

Неравенство выполнено, следовательно, теорема о треугольном неравенстве проверена.

Видео:Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Пример 3

Берём значение a = -2 и значение b = 5, то есть отрицательное число, а другое положительное, проверяем, выполняется ли неравенство.

Неравенство проверено, значит, теорема выполнена.

Видео:Неравенства треугольника. Практическая часть. 7 класс.Скачать

Пример 4

Выбираются следующие значения a = -2 и b = -5, то есть оба отрицательные числа, и мы проверяем, выполняется неравенство или нет.

Равенство проверено, следовательно, теорема о неравенстве Минковского выполнена.

Видео:Математика это не ИсламСкачать

Пример 5

Мы берем значение a = 0 и значение b = 5, то есть число ноль, а другое положительное, затем проверяем, выполняется неравенство или нет.

Равенство выполнено, следовательно, теорема о неравенстве треугольника проверена.

Видео:Доказательство свойств модуля, №25.Скачать

Пример 6

Мы берем значение a = 0 и значение b = -7, то есть число ноль, а другое положительное, затем проверяем, выполняется неравенство или нет.

Равенство проверено, следовательно, теорема о треугольном неравенстве выполнена.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Решенные упражнения

В следующих упражнениях изобразите геометрически неравенство треугольника или неравенство Минковского для чисел a и b.

Число a будет представлено как сегмент на оси X, его начало O совпадает с нулем оси X, а другой конец сегмента (в точке P) будет в положительном направлении (вправо) от оси X, если > 0, но если a 0), а точка Q будет | b | единиц слева от P, если b Предыдущая статья

4 Последствия английской революции

Как Карл Великий правил такой огромной империей?

💥 Видео

Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Неравенство Коши — Буняковского | Ботай со мной #049 | Борис Трушин |Скачать

Неравенство треугольникаСкачать

Геометрия - 7. Неравенство треугольника теория + практикаСкачать

#240. Неравенства Йенсена, о средних, Коши-Буняковского, ГёльдераСкачать

ГЕОМЕТРИЯ 7 класс : Неравенство треугольника | ВидеоурокСкачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать