Задачи на вектор умова пойнтинга

Мгновенное значение объемной плотности энергии электромагнитного поля в объеме dV в среде с параметрами е_а и р_а равно сумме объемных плотностей энергии электрического и магнитного полей, которые выражаются следующим образом:

В выражении (2.17) Е = E(t) и Н = H(_t) — мгновенные значения напряженностей электрического и магнитного полей электромагнитной волны. С учетом соотношения Н_т = E_m/Z_B, соотношений (2.8), (2.10), (2.13) выражение (2.17) запишется следующим образом:

Энергия, заключенная в объеме dV, будет равна

В выражении (2.18) dV = ds ? dl, где dV — элементарный объем, принимаемый в виде куба со сторонами dl; ds — площадь боковой поверхности куба. Волна, перемещающаяся в пространстве со скоростью о, за время dt пройдет участок длиной dl = udt. Удельная мощность потока энергии, пронизывающего элементарную площадку ds, будет равна

В выражении (2.19) записан модуль вектора удельной мощности потока энергии, пронизывающий элементарную площадку ds. Вектор удельной мощности потока энергии называется вектором Умова — Пойнтинга (в иностранной литературе он называется вектором Пойнтинга).

Вектор Умова — Пойнтинга направлен вдоль оси z и равен векторному произведению векторов Е и Н:

Он измеряется в В-А/м 2 или Вт/м 2 . Вектор направлен нормально к плоскости, образованной векторами Е и Н.

В соответствии с рис. 2.1 вектор Умова — Пойнтинга для мгновенных значений векторов напряженности электрического и магнитного полей будет направлен по оси z и по модулю будет равен

Положив начальные фазы векторов Е и Н равными (в выражении (2.15) это а_п и а₂₁), для фиксированного момента времени t = t₁ получим график распространения мгновенного значения вектора Умова — Пойнтинга вдоль координаты z, как показано на рис. 2.2. На рисунке показано среднее по времени

значение вектора S₀ =—Е_тН_т. Записанный в выражении

(2.20) вектор Умова — Пойнтинга для синусоидального процесса изменяется по синусоидальному закону с удвоенной частотой по сравнению с частотой изменения электрического и магнитного полей, как показано на рис. 2.2.

Рис. 2.2. Волновой характер распределения энергии

Вектор Умова — Пойнтинга в комплексной форме записи. Мощность энергии светового потока. Для расчета энергетических характеристик синусоидальных с периодом Т процессов в теории электромагнитного поля используются среднеквадратичные или действующие значения синусоидальных функций. Действующие значения характеризуют среднеквадратичные на периоде Т значения синусоидальных колебаний. Для синусоидальных функции напряженностей электрического и магнитного полей (2.14) действующие значения напряженностей электрического и магнитного полей запишутся следующим образом: 32

На комплексной плоскости векторы действующих значений напряженностей электрического и магнитного полей представляются векторами, длины которых пропорциональны действующему значению синусоидальной функции, с горизонтальной ось эти векторы составляют угол, равный начальной фазе синусоидальной функции. Представим синусоидальные функции напряженностей электрического и магнитного полей комплексами действующих значений E(t)—> Е_де^Е и Н(0->Н_де^н, где Ф_? — начальная фаза синусоидальной функции напряженности электрического поля, а ср_н — начальная фаза синусоидальной функции напряженности магнитного поля. В пространстве эти векторы задаются их проекциями на координатные оси х, у, z с единичными ортами i,j, к:

Вектор Умова — Пойнтинга для синусоидального процесса запишется следующим образом:

В формуле (2.21) Е_д — вектор действующего значения электрического поля, направленного в соответствии с рис. 2.1 по оси х, Н_д — вектор действующего значения напряженности магнитного поля, направленного по оси у.

Вектор Умова — Пойнтинга в комплексной форме записи S равен векторному произведению комплексных действующих значений векторов электрического и магнитного полей. При принятых направлениях векторов Е_д и Н_д он будет направлен по оси z.

Поток вектора S определяется выражением

В выражении (2.22) ds — это вектор, направление которого определяется нормалью к элементу ds поверхности s. В правой части равенства записано комплексное число, элементы которого Р и Q — это активная и реактивная мощности потока энергии, пронизывающей поверхность s. Символ; в этой записи — это мнимая единица, j = v-l. Следует обратить внимание на то, что поверхность s и вектор Умова — Пойнтин- га S обозначаются одинаковыми символами, как это принято в работах по теории электромагнитного поля.

Пример 2.3. Записать мгновенное значение модуля вектора Умова — Пойнтинга для условий задачи, сформулированной в примере 2.2.

Видео:Вектор Умова-Пойнтинга ● 3Скачать

Эквивалентность массы и энергии

Согласно принципу, лежащему в основе теории относительности, полная энергия физического объекта или системы физических тел определяется выражением

где Е — энергия объекта; т — его масса; с — скорость света в вакууме, с = 299 792 458 м/с.

В универсальной форме этот принцип был сформулирован в 1905 г. А. Эйнштейном. Связь инертных свойств объекта (системы физических тел) с его массой была установлена гораздо раньше рядом ученых.

В своей работе «Теория простых сред» (1873) Н. А. Умов получил соотношение массы и энергии в виде Е = ктс 2 , а в докторской диссертации в 1874 г. им были введены понятия потока энергии и мощности потока энергии через единицу поверхности. Джон Генри Пойнтинг в 1884 г. применил эти понятия к теории электромагнитного поля.

Видео:Вектор Умова-Пойнтинга ● 1Скачать

Вектор Пойнтинга (вектор Умова — Пойнтинга)

Перенос энергии бегущей упругой и электромагнитной волной определяют при помощи вектора, который называют вектором потока энергии. Этот вектор обозначим как $overline $(встречается обозначение $overline

$) Он показывает количество энергии, протекающее в волне за единицу времени через единицу площади поперечного сечения волны. Для электромагнитных волн данный вектор был введен Пойнтингом в 1884 г. Скорость переноса энергии при помощи вектора Пойнтинга не изменяется и равна характеристической скорости распространения электромагнитной волны в пространстве. Сейчас данный вектор ($overline$) называют вектором Умова — Пойнтинга.

Видео:Вектор Умова-Пойнтинга ● 2Скачать

Определение

Вектором Умова — Пойнтинга ($overline$) называют физическую величину, определяющую поток энергии электромагнитного поля, который равен:

где $overline$ — напряженность электрического поля; $overline$ — напряженность магнитного поля. Направлен $overline$ перпендикулярно $overline$ и $overline$ и совпадает с направлением распространения электромагнитной волны.

Видео:5 Вектор ПойтингаСкачать

Величина вектора Умова — Пойнтинга

Правая часть формулы (1) представляет собой векторное произведение векторов, значит, величина вектора Умова — Пойнтинга для электромагнитной волны равна:

где $alpha $ — угол между векторами $overline$ и $overline$, но $overlinebot $ $overline$, следовательно, получаем для электромагнитной волны:

Вектор $overline $удовлетворяет в свободном пространстве уравнению непрерывности:

где $w$ — объемная плотность энергии электромагнитного поля.

Видео:Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Вектор Умова — Пойнтинга плоской электромагнитной волны

В случае плоской электромагнитной волны величина вектора $overline$ равна:

где $u$ $=frac<sqrt<_0mu varepsilon _0>>$- фазовая скорость распространения электромагнитного возмущения в веществе с диэлектрической проницаемостью $varepsilon $ и магнитной проницаемостью $mu .$

где $c$ — скорость света в вакууме.

Мгновенные величины напряженности магнитного и электрического полей в рассматриваемой волне связаны соотношением:

выразим напряженность $H$:

Учитывая формулу (8) величину вектора $overline$ запишем как:

В изотропном веществе объемную плотность энергии электромагнитного поля найдем как:

Учитывая формулы (6) и (10) запишем еще одно выражение для величины вектора $overline$:

На практике переходят от мгновенных величин к их средним значениям. Для плоской электромагнитной волны средняя величина по времени вектора Умова — Пойнтинга равна:

Модуль величины $left|_tright|$ называют интенсивностью ($I$) электромагнитной волны:

Направление вектора Умова — Пойнтинга показывает направление движения энергии в электромагнитном поле. Если изобразить линии, касательные к которым в любой точке совпадут с направлениями вектора $overline$, то такие линии будут являться путями распространения энергии электромагнитного поля. В оптике это лучи.

Видео:Билет №38 "Поток энергии"Скачать

Примеры задач с решением

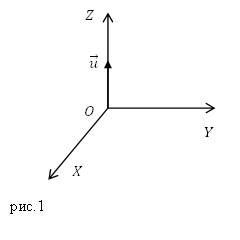
Задание. На рис.1 изображен вектор фазовой скорости плоской электромагнитной волны. В какой плоскости расположены векторы $overline$ и $overline$ полей этой волны?

Решение. Основой решения нашей задачи будем считать определение вектора $overline$:

Вектор $overline$ является результатом векторного произведения векторов$overline$ и $overline$, он направлен в сторону распространения электромагнитной волны, следовательно, $overlineuparrow uparrow overline$, для рис.1 вектор Умова — Пойнтинга направлен по оси Z. Значит, векторы $overlineи overline$ лежат в плоскости XOY.

Ответ. XOY

Задание. Запишите модуль среднего вектора Умова — Пойнтинга электромагнитной волны: $overline=E_0 $Считайте, что волна распространяется в вакууме по оси X.

Решение. Модуль вектора Умова — Пойнтинга для электромагнитной волны:

где $E$ и $H$ — мгновенные значения электрического и магнитного полей. Мгновенное значение вектора Умова — Пойнтинга будет равно:

[S=EH=E_0H_0<^2 left(omega t-kxright)(2.2), >]

где $H_0$ — амплитуда колебаний напряженности магнитного поля.

Средняя величина $_t$ может быть найдена:

принимая во внимание, что $<leftlangle <^2 left(omega t-kxright) >rightrangle >_t=frac$, для вакуума имеем:

Видео:Вектор Умова-Пойнтинга ● 5Скачать

Расчет вектора Умова-Пойнтинга и силы давления электромагнитной волны на однородный диэлектрический цилиндр Текст научной статьи по специальности « Физика»

Видео:Вектор Умова-Пойнтинга ● 4Скачать

Аннотация научной статьи по физике, автор научной работы — В.В. Котляр, А.Г. Налимов, Р.В. Скиданов

Рассмотрен алгоритм расчета дифракции электромагнитной монохроматической волны на диэлектрических микрообъектах имеющих размеры, сравнимые с длиной волны. Приведены сравнения численного моделирования расчета дифракции на микрообъектах для ТЕи ТМполяризацией с точным решением. С помощью данного алгоритма рассчитаны вектор Умова-Пойнтинга и сила давления непараксиальной цилиндрической гауссовой волны на круглый микро-цилиндр.

Видео:Лекция 25: Закон сохранения энергии. Вектор Умова-Пойнтинга.Скачать

Похожие темы научных работ по физике , автор научной работы — В.В. Котляр, А.Г. Налимов, Р.В. Скиданов

Видео:Средняя плотность потока энергии. вектор Пойнтинга.Скачать

CALCULATING OF THE UMOV-POITING VECTOR AND PRESSURE FORCE OF THE ELECTROMAGNETIC WAVE ON THE HOMOGENEOUS DIELECTRIC CYLINDER

Algorithm for calculating of diffraction of the electromagnetic monochromatic wave on the dielectric micro objects with the sizes same to wavelength is considered. Comparisons of the numerical modeling of diffraction of TEand TMpolarized waves on a micro objects with exact solving of this problem are presented. Using this algorithm Umov-Pointing vector and pressure force of the non-paraxial cylindrical Gaussian wave on the circle micro cylinder are calculated.

Видео:Вектор ПойнтингаСкачать

Текст научной работы на тему «Расчет вектора Умова-Пойнтинга и силы давления электромагнитной волны на однородный диэлектрический цилиндр»

РАСЧЕТ ВЕКТОРА УМОВА-ПОЙНТИНГА И СИЛЫ ДАВЛЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ НА ОДНОРОДНЫЙ ДИЭЛЕКТРИЧЕСКИЙ ЦИЛИНДР

© 2005 В.В. Котляр1, А.Г Налимов2, Р.В. Скиданов1

1 Институт систем обработки изображений РАН 2 Самарский государственный аэрокосмический университет

Рассмотрен алгоритм расчета дифракции электромагнитной монохроматической волны на диэлектрических микрообъектах имеющих размеры, сравнимые с длиной волны. Приведены сравнения численного моделирования расчета дифракции на микрообъектах для ТЕ- и ТМ- поляризацией с точным решением. С помощью данного алгоритма рассчитаны вектор Умова-Пойнтинга и сила давления непараксиальной цилиндрической гауссовой волны на круглый микро-цилиндр.

Обычно задачу манипуляции микрочастицами рассматривают для 3D случая, например, для частиц сферической формы. Впервые теоретическую задачу давления света на сферу с помощью теории Ми рассмотрел Де-бай в 1909 [1]. В общем случае сила давления света на микрочастицу должна рассматриваться с помощью максвелловского тензора напряжений электромагнитного поля [2]. Впервые сила давления слабосходящегося гауссова пучка на сферическую частицу с помощью теории Ми была оценена в [3], а для «острой» (непараксиальной) фокусировки гауссова пучка в [4,5]. Пользуются популярностью и приближенные методы расчета силы, действующей со стороны света на частицу: метод геометрической оптики с учетом фре-нелевских коэффициентов отражения и преломления [6], который применен для больших

значений параметра q = k0 а >> 1, где

— волновое число света в вакууме, а — радиус сферы, охватывающей объект, и метод градиентной и рассеивающей сил [7], применимый для рэлеевских частиц ^ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

2 , i2 i 12 И,, — E — H

Fz = — fí1 Z 8лЦ2

где к -— — волновое число света с длиной А

волны А. Аналогично (10) сила давления света с ТМ-поляризацией на 2D объект будет иметь следующие проекции

где dS; = -^dxdy , dSy =

F = -1 fJ 1 y 8л f I 2

dSz — ^х^у, Е1 — Ех, Е2 — Еу, Е3 — Ег (для

Hi и Ег. аналогично).

Перепишем выражения (9) для силы давления света на микрообъект в 2D случае. Для

ТЕ-поляризации ( Нх — Еу — Ег — 0 ) электрическое поле направлено вдоль оси X: Ех ^ 0, Z — оптическая ось, 2D-объект имеет вид цилиндра с произвольной формой сечения и имеет бесконечную протяженность вдоль оси X. Плоскость YOZ — плоскость падения света. В этом случае соотношение (9) примет вид:

2 2 2 EÁ — Ey — |И;|

Здесь £1 уже контур, охватывающий сечение

объекта в плоскости YOZ. Сила — направлена вдоль оптической оси и является аналогом рассеивающей силы для рэлеевских частиц [7], а Ку — направлена поперек оптической оси и является аналогом градиентной силы [7].

Связь между проекциями Ну, Нг и Ех следует из уравнений Максвелла:

+ RefeEy )dSy >, где (как и в уравнении (10))

dSy = nydl = sin tydl = dz

dSz = nzdl = cos Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

внутри объекта (у, г) е V и

фп+1( У, г) = уф0( ^ г) -у

3(ф„ (£, л) р(£, л)>3(н 02) (кЛ

нормали к контуру S, (у, г) е 5, 3 и 3-1 —

прямое и обратное 2D Фурье-преобразования. г / „ , ,

. снаружи объекта (у, г)£V , где ф, и ф —

Аналогично, интеграл типа свертки по площади объекта V в (13) и (14) можно перепи- рассчитанные комплексные амплитуды поля сать через преобразование Фурье с помощью функции объекта

на (п+1)-й и (п)-й итерациях, у — параметр релаксации.

Для проверки работоспособности алго-

ритма проводилось численное сравнение по-

Итеративный алгоритм решения интегрального уравнения (13) будет иметь вид:

ф п+1( У, г) = уф0( У, г)в-у

лей дифракции плоской ТМ-поляризованной волны на круглом диэлектрическом цилиндре, рассчитанных с помощью полученного алгоритма и с помощью известных аналитических формул.

5 10 15 20 25 30 35 40 45 50 55 60 65 70 Ы итерации

5 10 15 20 25 30 35 40 45 50 55 60 65 70 Ы итерации

Рис. 1. а — среднеквадратичное отклонение модуля амплитуды магнитного поля, рассчитанного данным алгоритмом, от точного решения в зависимости от числа итераций; б — среднеквадратичное отклонение двух модулей амплитуд магнитного поля, рассчитанных данным алгоритмом, для двух соседних итераций, в зависимости от номера итерации

Если сравнить данные графики (рис. 1) с аналогичными, полученными для ТЕ поляризации [12], можно заметить, что устойчивость алгоритма для ТМ поляризации выше, чем для ТЕ, но точность ниже. Это обусловлено ошибкой расчета интеграла по контуру объекта на границе раздела двух сред.

Параметр релаксации у был подобран экспериментально для случая дифракции на круглом цилиндре. Подбор был осуществлен на поле 256×256 отсчетов, 2,5×2,5 мкм. Диаметр цилиндра был равен длине волны в d = X=1 мкм, диэлектрическая постоянная цилиндра, находящегося в вакууме, в =2. При этих параметрах среднеквадратичное отклонение рассчитанного за 13 итераций модуля амплитуды напряженности магнитного поля от точного решения в зависимости от параметра у показано на рис. 2.

Как видно из рис. 2, достаточно широкий диапазон параметра у приводит к устойчивой работе алгоритма, наилучшим являет-

S 0 3 0. 35 0 4 0. 45 0 5 0. 55 /

Рис. 2. Зависимость невязки на 13-ой итерации от коэффициента у

ся у =0,35..0,4. Экспериментально было найдено, что алгоритм не расходится при усло-

— ni Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

I ехр|» Т^Г + Й + Ул/1 2 , (22)

где а 0 — параметр гауссова пучка, связанный

с радиусом его перетяжки ю соотношением: =

Силы, расчитанные по формуле (10), действующие на круглый цилиндр в случае ТЕ-поляризованной волны, представлены на рис. 5. Параметры эксперимента: все поле 10×10 мкм, 512×512 отсчетов, длина волны X = 1 мкм, диаметр цилиндра D=1 мкм, диэлектрическая проницаемость объекта £ =2, диэлектрическая проницаемость среды £ 0=1, радиус перетяжки пучка в фокусе а =0,5 мкм. Смещение от центра L имеет размерность мкм. Силы даны в безразмерных единицах.

Аналогичные силы в случае ТМ-поляри-зации, рассчитанные по формуле (12), представлены на рис. 6.

Рис. 5. ТЕ-поляризация: а — зависимость силы Fz от смещения L объекта вдоль оси Z через центр перетяжки ^=0); б — зависимость сил Fz и FУ от смещения L объекта вдоль оси Y через центр перетяжки ^=0)

В работе получены следующие результаты: разработан итеративный алгоритм для быстрого расчета поля дифракции ТМ-по-ляризованной электромагнитной волны на цилиндрических диэлектрических микрообъектах;

с помощью быстрого преобразования Фурье за 74 итераций, которые на компьютере Celeron 1000 MHz выполняются за 1 минуту 18 секунд, было рассчитано поле дифракции плоской волны на круглом цилиндре, отличающееся от точного решения в среднем на 4%;

численно показано, что параметр релаксации у итеративного алгоритма можно варьировать в широком диапазоне 0,3 Надоели баннеры? Вы всегда можете отключить рекламу.

📸 Видео

Энергия течёт в пространстве а не в проводе Вектор Умова ПойтингаСкачать

Вектор ПойнтингаСкачать

вектор Пойнтинга 1Скачать

Вектор Умова Пойтинга или откуда берётся энергия в электромагнетизмеСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Вектор Пойнтинга и энергия конденсатораСкачать

Урок 225. Задачи на поток вектора напряженности электрического поляСкачать