Задачи на тему параллельные и перпендикулярные прямые

Конспект урока

Параллельные и перпендикулярные прямые

Перечень рассматриваемых вопросов:

• Взаимное расположение прямых на плоскости.
• Параллельные прямые.
• Аксиома параллельных прямых.
• Перпендикулярные прямые.
• Расстояние от точки до прямой, между параллельными прямыми.

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Перпендикулярные прямые – две прямые называются перпендикулярными, если при пересечении они образуют четыре прямых угла.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Взаимное расположение двух прямых на плоскости.

Вспомните, как могут располагаться на плоскости две прямые.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Аксиома параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Углы, изображенные на рисунке:

Накрест лежащие: 3 и 5; 4 и 6.

Соответственные: 1 и 5; 2 и 6; 3 и 8; 4 и 7.

Односторонние: 3 и 6; 4 и 5.

Признаки и свойства параллельных прямых.

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Это признаки параллельности прямых. Обратные теоремы верны и представляют свойства параллельных прямых.

Способ построения параллельных прямых:

Аксиома параллельных прямых.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Если две прямые параллельны третьей, то они параллельны.

Если две прямые, пересекаясь, образуют четыре прямых угла, они называются перпендикулярными.

Прямые а и b на рисунке перпендикулярны: а ⏊ b.

Через каждую точку можно провести прямую, перпендикулярную данной и притом только одну.

Это можно сделать, пользуясь угольником или транспортиром.

Перпендикулярность и параллельность прямых.

Две прямые, перпендикулярные к третьей не пересекаются т. е параллельны между собой.

Отрезок АВ, перпендикулярный к прямой а, называют перпендикуляром. Точка В – основание перпендикуляра.

Из любой точки, не лежащей на данной прямой, можно опустить перпендикуляр на эту прямую и притом только один.

Длину перпендикуляра АВ называют расстоянием от точки А до прямой а.

Расстоянием между параллельными прямыми называют расстояние АВ от любой точки одной прямой до другой прямой.

Разбор заданий тренировочного модуля.

1. Решение: ∠1 и ∠2 соответственные, по свойству параллельных прямых: ∠1 = ∠2 = 220°: 2 = 110°.
2. ∠2 и ∠3 смежные, по свойству смежных углов: ∠2 + ∠3 = 180° значит, ∠3 = 180° – 110° = 70°.

№ 2. Докажите, что биссектрисы смежных углов перпендикулярны.

1. Пусть ∠АОВ и ∠ВОС – смежные углы. ОК и ОР – их биссектрисы.
2. ∠KOP = ∠КОВ + ∠ВОР. Поскольку ОК и ОВ – биссектрисы, то ∠КОВ = 1/2∠АОВ, ∠ВОР = 1/2∠ВОС по определению биссектрисы.
3. Тогда ∠КОР = 1/2∠АОВ + 1/2∠ВОС = 1/2(∠АОВ + ∠ВОС) = 180° : 2 = 90°.
4. Итак, ОК ⏊ ОР т. е. прямые перпендикулярны.

Видео:Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы рассмотрим перпендикулярность прямых в пространстве, перпендикулярность прямой и плоскости и параллельные прямые, которые перпендикулярны к плоскости.
Вначале дадим определение двух перпендикулярных прямых в пространстве и их обозначение. Рассмотрим и докажем лемму о параллельных прямых, перпендикулярных третьей прямой. Далее дадим определение прямой, перпендикулярной к плоскости, и рассмотрим свойство такой прямой, при этом вспомнив взаимное расположение прямой и плоскости. Далее докажем прямую и обратную теорему о двух параллельных прямых, перпендикулярных к плоскости.
В конце урока решим две задачи на перпендикулярность прямых в параллелепипеде и тетраэдре.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Обобщающее повторение курса геометрии 7-9 класс. Параллельные прямые. Перпендикулярные прямые

Видео:Перпендикулярные прямые. 6 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

ОБОБЩАЮЩЕе ПОВТОРЕНИЮ ГЕОМЕТРИИ
(7–9 классы)

I. Углы. Параллельные прямые. Перпендикулярные прямые (2 часа).

1. Угол. Градусная и радианная мера углов. Построение угла, равного данному. Построение биссектрисы угла. Смежные углы и их свойства.

Вертикальные углы и их свойства.

2. Параллельные прямые. Существование и единственность прямой, параллельной данной и проходящей через точку вне ее (аксиома).

Признаки параллельности прямых.

Теоремы об углах, полученных при пересечении двух параллельных прямых третьей.

3. Перпендикулярные прямые. Существование и единственность перпендикуляра к прямой, проведенного через данную точку.

Построение прямой, перпендикулярной данной.

Геометрическое место точек, равноудаленных от двух данных. Деление отрезка пополам.

4. Расстояния: между двумя точками; от точки до прямой; между параллельными прямыми.

II. Треугольники (3 часа).

1. Соотношение между сторонами и углами треугольника.

Средняя линия треугольника.

Биссектриса угла треугольника и ее свойства.

Равные треугольники. Признаки равенства треугольников.

Подобные треугольники. Признаки подобия треугольников.

2. Равнобедренный треугольник. Теорема об углах при основании равнобедренного треугольника и теорема, обратная ей. Свойства медианы, биссектрисы и высоты равнобедренного треугольника, проведенных к его основанию. Сумма углов треугольника. Свойства внешнего угла треугольника.

3. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников. Признаки подобия прямоугольных треугольников.

Перпендикуляр, наклонная и ее проекция.

Средние пропорциональные в прямоугольном треугольнике.

4. Синус, косинус и тангенс острого угла в прямоугольном треугольнике.

Значение синуса, косинуса и тангенса некоторых углов.

Решение прямоугольных треугольников. Основные тригонометрические тождества.

5. Теорема косинусов.

III. Четырехугольники (2 часа).

1. Параллелограмм. Прямоугольник. Ромб. Квадрат. Определение. Признаки параллелограмма. Свойства параллелограмма. Свойства прямоугольника, ромба, квадрата. Площадь параллелограмма, прямоугольника, ромба, квадрата.

2. Трапеция. Свойства средней линии трапеции, площадь трапеции.

IV. Многоугольник. Окружность. Круг (2 часа).

1. Выпуклый многоугольник, сумма углов выпуклого многоугольника. Внешний угол выпуклого многоугольника.

2. о кружность, круг. Уравнение окружности. Касательная к окружности и ее свойства. Длина окружности.

Центральный угол и дуга окружности.

3. Вписанный и описанный многоугольник.

Расположение центров окружностей, описанной около треугольника и вписанной в треугольник.

Формулы, выражающие радиус окружности, описанной около треугольника, и радиус окружности, вписанной в треугольник, через длины сторон и площадь.

Правильный многоугольник. Теорема о существовании для правильного многоугольника окружности, описанной около него, и окружности, вписанной в него. Совпадение центров окружностей, описанной около правильного многоугольника и вписанной в него.

Формулы, связывающие сторону правильного многоугольника с радиусом описанной около него окружности и радиусом вписанной в него окружности, их частные случаи для n = 3, 4, 6.

4. Площадь круга и его частей.

5. Углы, вписанные в окружность.

V. Преобразование фигур (1 час).

1. Движение. Виды движений: симметрии относительно точки, симметрия относительно прямой, поворот, параллельный перенос.

2. Преобразование подобия. Гомотетия. Подобие фигур. Отношение площадей подобных фигур. Отношение периметров подобных фигур.

VI. Векторы на плоскости (1 час).

1. Векторы и его окружность. Равные векторы. Условие равенства векторов, заданных геометрически, условие равенства векторов, заданных координатами. Откладывание вектора, равного данному, от заданной точки.

2. Сложение и вычитание векторов в координатной и геометрической формах. Умножение вектора на число в координатной и геометрической формах.

Коллинеарные векторы, условие коллинеарности векторов, заданных координатами. Выражение вектора через … .

3. Скалярное произведение векторов, заданных в координатной и геометрической формах, нахождение угла между векторами, заданными координатами. Условие перпендикулярности векторов.

У роки 1–2
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ.
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ

Цели: обобщить и систематизировать знания и умения, усвоить системы опорных знаний и умений, углубить знания в пределах темы.

I. Актуализация опорных теоретических знаний.

Учащиеся работают в группах из 4 человек. Учебные группы сформированы из учащихся с неравными возможностями.

На каждом столе имеются: вопросы по обозначенной теме (раздел I); тематические таблицы, составленные в 7 классе; предметный указатель из учебника (желательно ксерокопии).

Из учащихся с высокими учебными возможностями можно создать отдельную группу, они могут самостоятельно повторить теорию, составить опорную таблицу и приступить к решению задач.

Углы. Параллельные прямые.
Перпендикулярные прямые

Внутренние накрест лежащие углы – 3 и 5, 4 и 6, односторонние углы – 4 и 5, 3 и 6, соответственные углы – 1 и 5, 4 и 8, 2 и 6, 3 и 2.

Задачи на построение: угла, равного данному; биссектрисы угла; перпендикулярной прямой; деление отрезка пополам.

Определение: а и в не пересекаются.

Признаки
параллельности
(прямая теорема)

Свойства
(обратная теорема)

2. Если а || в , то  1 =  2

3. Если  1 +  2 =
= 180°, то а || в

2. Если а || в , то  1 +  2 = 180°

Определение: АВ  СD:  АОD =  СОВ =  АОС =  DОВ = 90°.

Н – основание перпендикуляра;

В – основание наклонной.

АН – расстояние от точки А до прямой а.

II. з адачи для устного решения.

– что угол, смежный с тупым углом, – тупой;

– угол, смежный с прямым углом, прямой;

– если два угла сложные, то они прямые;

– если два угла смежны с одним тем же углом, то они равны?

2. Если две параллельные прямые пересечены секущей,

– то сумма односторонних углов равна 180°;

– сумма накрест лежащих углов равна 180°;

– соответственные углы могут быть тупыми;

– односторонние углы могут быть острыми;

– среди образовавшихся углов есть не менее четырех равных;

– среди образовавшихся углов есть ровно четыре равных угла.

3. Может ли при пересечении двух прямых образоваться:

– четыре прямых угла;

– четыре острых угла;

– три тупых и один острый угол;

– два прямых и два тупых угла?

– две прямые, имеющие общую точку, быть параллельными третьей прямой;

– две прямые, параллельные третьей, иметь общую точку;

– две прямые, перпендикулярные третьей, быть перпендикулярными;

– две прямые, перпендикулярные третьей, быть параллельными?

III. Задачи на готовых чертежах.

Дано :  1 =  4. Дано :  1 +  2 = 180°.

Доказать :  2 =  3. Доказать : 1)  АВС =  АСЕ;

Дано :  1 =  2. Дано :  2 =  3.

Доказать :  ВАС +  АСD = Доказать : 1)  1 =  3;

= 180°. 2)  3 +  4 = 180°.

Найти :  ВОС Дано :  АОВ = (  ВОС +

Найти : 1)  АОВ,  ВОС,

Дано:  АВЕ =  СВЕ.

Дано : АВ || DЕ. Дано : а || в . Доказать : АВ || СD.

Доказать :  1 + Доказать :

III. Тест по теме «Углы. Параллельные прямые. п ерпендикулярные прямые».

1. Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами.

а) 24°; б) 30°; в) 36°; г) 40°.

2. Разность между двумя односторонними углами при параллельных а и в и секущей с равна 24°. Найдите больший из этих углов.

3. Прямые АВ и СD пересекаются в точке Е, причем сумма углов ВЕС и АЕD равна 194°. Найдите угол АЕС.

а) 97°; б) 83°; в) 117°; г) 73°.

4. Углы ВОD и СОD – смежные. ОЕ – биссектриса угла ВОD, причем угол СОD на 21° больше угла DОЕ. Найти угол ВОЕ.

а) 67°; б) 74°; в) 46°; г) 56°.

5. Прямые MN и РК пересекаются в точке Е, ЕС – биссектриса угла МЕР,  СЕК = 137°. Найдите угол КЕМ.

а) 108°; б) 84°; в) 94°; г) 82°.

а) 114°; б) 112°; в) 102°; г) 124°.

6. Дано: СД  АК, MN  АК,  AMN = 28°, CЕ – биссектриса  ВСD.

а) 92°; б) 104°; в) 114°; г) 98°.

1. Величины смежных углов пропорциональны числам 4 и 11. Найдите разность между этими углами.

а) 84°; б) 76°; в) 96°; г) 68°.

2. Разность между двумя внутренними односторонними углами при параллельных прямых а и в с секущей с равна 46°. Найдите больший из этих углов.

а) 126°; б) 123°; в) 113°; г) 136°.

3. Прямые MN и КР пересекаются в точке О, причем сумма углов КОМ и NOP равна 134°. Найдите величину угла КОN.

а) 44°; б) 46°; в) 113°; г) 67°.

4. Углы АОМ и СОМ – смежные. ОК – биссектриса угла АОМ, причем угол АОК в 4 раза меньше, чем угол СОМ. Найдите угол КОМ.

а) 45°; б) 30°; в) 36°; г) 40°.

5. Прямые АВ и СD пересекаются в точке О, ОК – биссектриса угла АОD,  СОК = 118°. Найдите угол ВОD.

а) 59°; б) 64°; в) 68°; 56°.

6. Дано: АВ  ЕD, КМ  ЕD,  АВЕ = 34°. MN – биссектриса  КМС.

📽️ Видео

Параллельные прямые. 6 класс.Скачать

Параллельные и перпендикулярные прямые.Скачать

Математика 6 класс: Параллельные и перпендикулярные прямыеСкачать

Перпендикулярные прямые. Практическая часть. 6 класс.Скачать

Перпендикулярные и параллельные прямые. Математика 6 классСкачать

Перпендикулярные прямые. Практическая часть. 6 класс.Скачать

Параллельные и перпендикулярные прямые. 5 классСкачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

6 класс, 44 урок, Параллельные прямыеСкачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Задача о перпендикулярных прямых. Геометрия 7 класс.Скачать

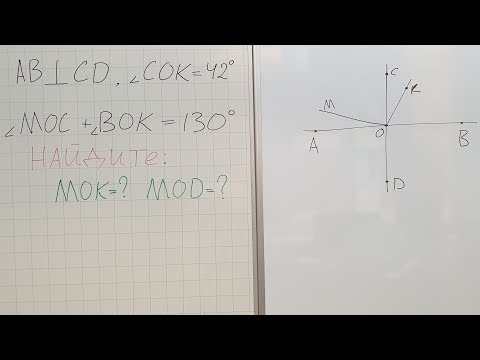
7 класс, 12 урок, Перпендикулярные прямыеСкачать

Параллельные прямые (задачи).Скачать

Как провести множество параллельных или перпендикулярных прямых без транспортира?Скачать

Перпендикулярные прямыеСкачать