| Фигура | Рисунок | Формулировка | ||||||||
| Прямоугольный треугольник | ||||||||||
| Равнобедренный прямоугольный треугольник | ||||||||||
| Прямоугольный треугольник с углом в 30° |
| Прямоугольный треугольник |
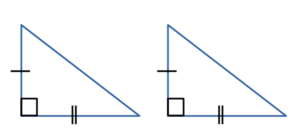
| Равнобедренный прямоугольный треугольник |
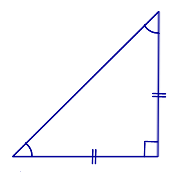 Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45° . |
| Прямоугольный треугольник с углом в 30° |
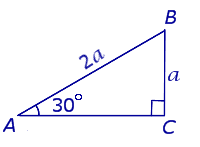 Свойство прямоугольного треугольника с углом в 30° : Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30° : Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° . |
| Медиана, проведённая к гипотенузе прямоугольного треугольника |
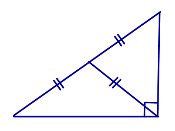 Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. |
| Центр описанной окружности |
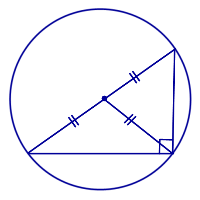 Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. |
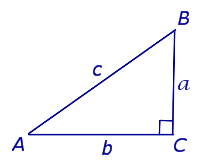 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным Содержание Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать  Прямоугольный треугольник: Признаки Равенства и ПодобияВидео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать  ОпределениеПрямоугольный треугольник — это треугольник, в котором один из углов прямой.
Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать  Свойства прямоугольного треугольникаВ прямоугольном треугольнике:
Формулы:
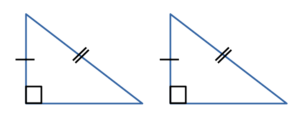
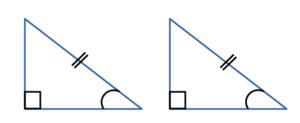
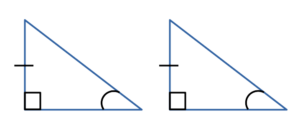
Видео:Центр окружности, описанной около треуг ABC лежит на стороне AB Радиус равен 25 Найти AC если BC=48Скачать  Признаки равенства прямоугольных треугольников
Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать  Признаки прямоугольного треугольника
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  Признаки подобия прямоугольных треугольников
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Если центр описанной окружности лежит на стороне треугольникаЕсли центр описанной около треугольника окружности лежит на стороне треугольника, то этот треугольник — прямоугольный. Сторона, на которой лежит центр описанной окружности, является гипотенузой. Доказать : ∆ABC — прямоугольный, AB — хорда проходящая через центр окружности. Значит, AB — диаметр. Значит, треугольник ABC — прямоугольный, AB — гипотенуза. Что и требовалось доказать . Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найти AC, если BC=32. Так как центр описанной около треугольника окружности ABC окружности лежит на стороне AB, то ABC — прямоугольный треугольник с гипотенузой AB. 📽️ ВидеоГеометрия. Теорема Пифагора. ОГЭ по математике. Задание 16Скачать  15 задание треугольники огэ по математике / маттаймСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Задача№25 ОГЭ Точка M и N лежат на стороне АС. Найдите радиус окружности, если cos ВАС ...Скачать  16 задание ОГЭ 2023 Окружность Треугольник #Shorts #огэпоматематике2023 #геометрия #окружностьСкачать  найти угол треугольника вписанного в окружность с центром на сторонеСкачать  ✓ Квадрат вписан в прямоугольный треугольник | Ботай со мной #129 | Борис ТрушинСкачать  №17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать  Задания с окружностью, тестовая часть ОГЭ (2 серия)Скачать  Вершины K и L квадрата KLMN с центром O лежат на стороне AB треугольника ABC.Скачать  Урок 3. №23 ОГЭ. Касательная. Окружность с центром на стороне AC касается АВ в точке В.Скачать  Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать  ОГЭ 2021 задание №17 окружностьСкачать  |

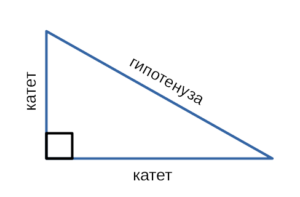
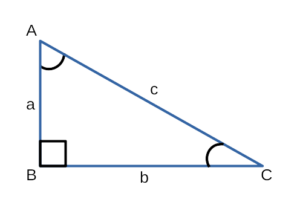
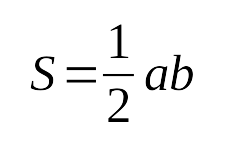
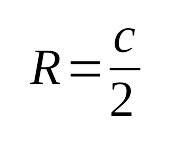
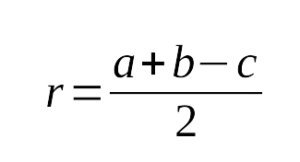
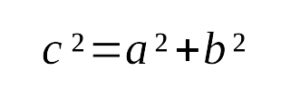
 Дано : ∆ABC, окружность (O: R) — описанная, O∈AB
Дано : ∆ABC, окружность (O: R) — описанная, O∈AB Дано : ∆ABC, окружность (O: R) — описанная, O∈AB, R=20, BC=32
Дано : ∆ABC, окружность (O: R) — описанная, O∈AB, R=20, BC=32