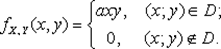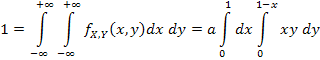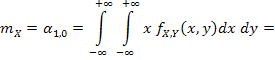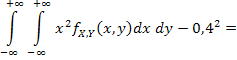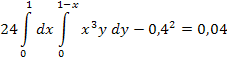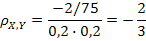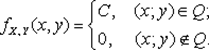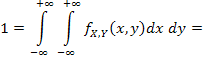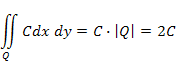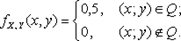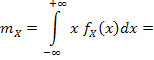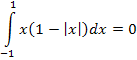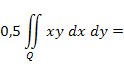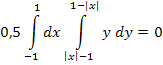Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю — двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.
Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать
Система непрерывных случайных величин: теория
Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:
Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:
Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:
$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$
Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:
Если для всех значений $(x,y)$ выполняется равенство
то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).
Видео:Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать
Примеры решений
Задача 1. Дана плотность распределения вероятностей системы $$ f(x)= left< begin C, mbox O(0,0), A(4,0), B(4,1)\ 0, mbox \ end right. $$ Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_, F(2,10), M[X|Y=1/2]$.
Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ — плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt, quad A(0;0), B(-1;-1), C(-1;0) $$
Задача 3. Интегральная функция распределения случайного вектора (X,Y): $$ F(x)= left< begin 0, mbox x le 0 mbox yle 0\ (1-e^)(1-e^), mbox x gt 0 mbox ygt 0\ end right. $$ Найти центр рассеивания случайного вектора.
Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У) $$f(x,y)=C e^$$ Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.
Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).
Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.
Задача 7. Плотность вероятности системы случайных величин равна $$f(x,y) = c(R-sqrt), quad x^2+y^2 lt R^2.$$ Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.
Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y $$f(x,y)=frac.$$ Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_$.
Видео:Случайный вектор двумерной случайной величиныСкачать
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Видео:Теория вероятностей | Математика TutorOnlineСкачать
Ковариация и коэффициент корреляции
Начальным моментом порядка k + s системы двух случайных величин (X;Y) называется действительное число 
, определяемое по формуле:
| (8.14) |  |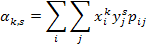
если (X;Y) — система двух дискретных случайных величин;
| (8.15) |  |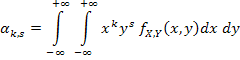
если (X;Y) — система двух непрерывных случайных величин.
Центральным моментом порядка k + s системы двух случайных величин (X;Y) называется действительное число 
, определяемое по формуле:
| (8.16) |  |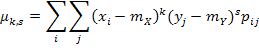
если (X;Y) — система двух дискретных случайных величин;
| (8.17) |  |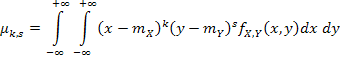
если (X;Y) — система двух непрерывных случайных величин.
На практике чаще всего встречаются моменты первого и второго порядков. Очевидно, что начальные моменты первого порядка есть не что иное, как математические ожидания компонент X и Y:
| (8.18) |  ,  . |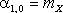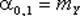
Точка с координатами (mX; mY) на плоскости xOy представляет собой характеристику положения случайной точки (X;Y), а ее рассеивание (разброс) происходит вокруг (mX; mY).
Центральные моменты первого порядка, очевидно, равны нулю, т.е.
| (8.19) |  |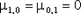
Имеются три начальных момента второго порядка — 
, 
и 
. Причем первые два из них есть не что иное, как начальные моменты второго порядка компонент X и Y:
| (8.20) |  ,  . |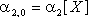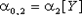
Имеются три центральных момента второго порядка 
, 
и 
. Первые два из них представляют собой дисперсии компонент X и Y соответственно:
| (8.21) |  ,  . |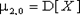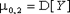
Рассмотрим 
отдельно.
Центральный момент второго порядка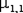 
называется ковариацией случайной величины (X;Y) .
Для момента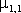 
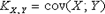
используется обозначение 
.
Замечание. По определению ковариации: KX,Y = KY,X.
В механической интерпретации, когда распределение вероятностей на плоскости xOy трактуется как распределение единичной массы на этой плоскости, точка (mX; mY) есть не что иное, как центр масс распределения; дисперсии D[X] и D[Y] — моменты инерции распределения относительно точки (mX; mY) в направлении осей Ox и Oy соответственно, а ковариация — это центробежный момент инерции распределения масс.
Теорема. Если случайные величины X и Y независимы, то KX,Y = 0 .
Замечание. Как правило, KX,Y удобнее вычислять по формуле 
.
Ковариация KX,Y характеризует не только степень зависимости двух случайных величин (X;Y) , но также их рассеивание вокруг точки (mX; mY). Однако размерность ковариации KX,Y равна произведению размерностей случайных величин X и Y. Чтобы получить безразмерную величину, характеризующую только зависимость, а не разброс, ковариацию KX,Y делят на произведение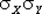 
:
| (8.22) |  |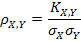
Величина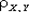 
называется коэффициентом корреляции случайных величин X и Y.
Коэффициент корреляции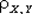 
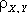
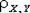
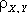
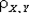
характеризует степень зависимости случайных величин X и Y, причем не любой зависимости, а только линейной, проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (или убывать). В первом случае 
> 0 и говорят, что случайные величины X и Y связаны положительной корреляцией, во втором случае 
0, = -1 при a 0; 2) 
= -1, т.к. a = -7, a
Поскольку между случайными величинами X и Y имеется линейная связь Y = 7 — X, то 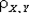= -1.
Ответ. 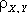= -1.
Теорема. Для любых случайных величин X и Y: | 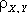| £ 1.
Определение. Случайные величины X и Y называются некоррелированными, если 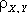=0 (или KX,Y = 0 ), иначе X и Y называются коррелированными.
Замечание. Из независимости случайных величин следует их некоррелированность. Но из некоррелированности ( 
= 0) не вытекает их независимость. Действительно, если 
= 0, то это означает только отсутствие линейной связи между случайными величинами, однако любой другой вид связи может при этом присутствовать.
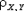
Пример. Закон распределения случайного вектора (X;Y) задан таблицей:
| XY | |
| 0,1 | 0,2 |
| 0,3 | |
| 0,1 | 0,3 |
Выяснить, зависимы или нет случайные величины X и Y. Найти: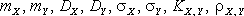 
.
Решение. Найдем законы распределения компонент X и Y:
| XY | pi | ||
| 0,1 | 0,2 | 0,3 | |
| 0,3 | 0,3 | ||
| 0,1 | 0,3 | 0,4 | |
| pj | 0,2 | 0,6 | 0,2 |
Очевидно, что компоненты X и Y являются зависимыми, т.к.
mX = 1 × 0,3 + 2 × 0,3 + 4 × 0,4 = 2,5.
mY = 0 × 0,2 + 2 × 0,6 + 5 × 0,2 = 2,2.
DX = 1 2 × 0,3 + 2 2 × 0,3 + 4 2 × 0,4 — 2,5 2 = 1,65,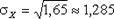 
.
DY = 0 2 × 0,2 + 2 2 × 0,6 + 5 2 × 0,2 — 2,2 2 = 2,65,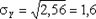 
.
KX,Y = 
1,1 — 1,0 × 0,1 = 1 × 0 × 0,1 + 1 × 2 × 0 + 1 × 5 × 0,2 + 2 × 0 × 0 + 2 × 2 × 0,3 + 2 × 5 × 0 + 4 × 0 × 0,1 + 4 × 2 × 0,3 + 4 × 5 × 0 — 2,5 × 2,2 = -0,9.
.
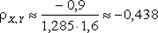
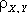
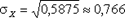
Так как 2 × 0,2 + 0 2 × 0,35 + 1 2 × 0,45 — 0,25 2 = 0,5875, 
.
DY = 1 2 × 0,8 + 2 2 × 0,2 — 1,2 2 = 0,16,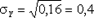 
.
KX,Y = 1,1 — 1,0 × 0,1 = -1 × 1 × 0,15 + (-1) × 2 × 0,05 + 0 × 1 × 0,3 + 0 × 2 × 0,05 + 1 × 1 × 0,35 + 1 × 2 × 0,1 — 0,25 × 1,2 = 0; = 0.
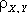
Этот пример показывает, что случайные величины X и Y могут быть некоррелированными, но при этом являться зависимыми.
Пример. Двумерный случайный вектор (X;Y) подчинен закону распределения с плотностью
Область D — треугольник, ограниченный прямыми x + y — 1 = 0, x = 0, y = 0.
Найти: коэффициент а, 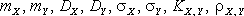. Выяснить, зависимы или нет случайные величины X и Y.
Решение. Коэффициент a находится из уравнения
Опуская промежуточные выкладки (в этом примере будем делать так и в дальнейшем), получаем a = 24. Далее:
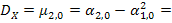
Заметим, что в силу симметрии по переменным x и y, можно не вычислять математическое ожидание и дисперсию компоненты Y, т.е. mY = mX = 0,4, DY = DX = 0,04. Тогда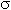 
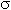
X = Y = 0,2.
Вычислим ковариацию и коэффициент корреляции:
; 
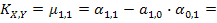
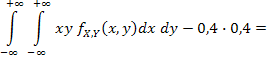
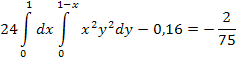
Поскольку компоненты X и Y коррелированны, следовательно, они зависимы.
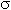
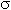
Ответ. a = 24, mY = mX = 0,4, DY = DX = 0,04, X = Y = 0,2, KX,Y = -2/75. Компоненты X и Y зависимы.
Пример. Двумерный случайный вектор (X;Y) равномерно распределен на множестве случайных точек Q, задаваемых неравенством |x| + |y| £ 1. Выяснить, являются ли случайные величины X и Y: 1) зависимыми; 2) коррелированными.
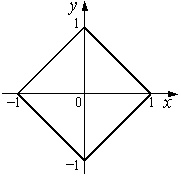
Рис. 8.6. Множество точек Q, задаваемых неравенством |x| + |y| £ 1
Решение. Множество точек Q, задаваемых неравенством |x| + |y| £ 1, является квадратом (рис. 8.6). Поскольку двумерный случайный вектор (X;Y) равномерно распределен на множестве Q, его плотность имеет вид
Из условия нормировки найдем константу C:
где |Q| — площадь квадрата Q, равная 2. Отсюда C = 0,5, а значит,
1) Найдем вначале плотность распределения компоненты X.
, т.е. 
.
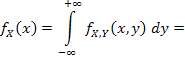
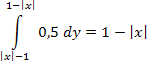
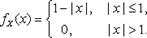
Аналогично находится плотность распределения компоненты Y:
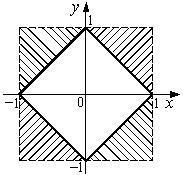
Рис. 8.7. Равенство fX,Y(x,y) = fX(x) × fY(y) не выполняется для точек координатной плоскости заштрихованных областей
Равенство fX,Y(x,y) = fX(x) × fY(y) не выполняется для точек координатной плоскости, принадлежащих заштрихованным областям (рис. 8.7), поскольку в этих точках fX,Y(x,y) = 0, а fX(x) ¹ 0 и fY(y) ¹ 0. Суммарная площадь заштрихованных областей равна 2, значит, компоненты X и Y зависимы.
2) Вычислим математические ожидания компонент X и Y:
т.к. интеграл от нечетной функции в симметричных пределах равен нулю. Аналогично mY = 0 .
Определим начальный момент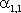 
:
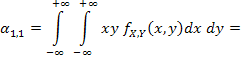
Таким образом, ковариация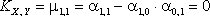 
. Значит, компоненты X и Y некоррелированные.
Ответ. компоненты X и Y зависимы, но некоррелированны.
Видео:Функция распределения дискретной случайной величиныСкачать
Распределение случайного вектора
Распределения векторных случайных величин представляются теми же основными формами, что и распределения скалярных. В дальнейшем ограничимся рассмотрением этих форм применительно лишь к двумерному случайному вектору (системе двух случайных величин).
Функция вероятности используется только для случайных векторов с дискретными компонентами и обычно задается таблицей, где указываются возможные значения х. и у. компонент X и Y случайного вектора , а также вероятности р(х., у.) всех пар этих значений (табл. 2.3).
Очевидно, что при этом 
🔥 Видео
Непрерыный случайный вектор и его характеристикиСкачать
Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать
Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать
Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать
Корреляция и ковариация двумерной случайной величиныСкачать
Зависимость компонент двумерного распределенияСкачать
Нахождение функции распределения для двумерного случайного вектора по плотностиСкачать
Нахождение функции случайного вектораСкачать
Математическое Ожидание, Дисперсия, Стандартное Отклонение за 5 минутСкачать
Лекция по теорверу и матстату №8.Числовые характеристики случайных векторов. Ковариация, еёсвойства.Скачать
Двумерное дискретное распределениеСкачать
Функция распределения и плотность распределенияСкачать
Нормальное Распределение за 6 МинутСкачать
Семинар "Непрерывные случайные векторы" от 09.11.2020Скачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
