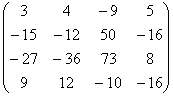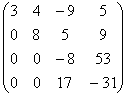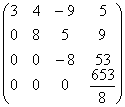Вычислить норму вектора в l1

Дата публикации 2018-02-05

Вычисление длины или величины векторов часто требуется либо непосредственно как метод регуляризации в машинном обучении, либо как часть более широких векторных или матричных операций.

В этом уроке вы узнаете, как рассчитать длину или величину вектора, называемую векторной нормой.

После завершения этого урока вы узнаете:

• Норма L1, которая рассчитывается как сумма абсолютных значений вектора.
• Норма L2, которая рассчитывается как квадратный корень из суммы квадратов векторных значений.
• Максимальная норма, которая рассчитывается как максимальные значения вектора.

• Обновление март / 2018: Исправлена ​​опечатка в уравнении максимальной нормы.
• Обновление сентябрь / 2018: Исправлена ​​опечатка, связанная с размером заданных векторов.

Видео:Норма вектора. Часть 1.Скачать

Обзор учебника

Этот урок разделен на 4 части; они есть:

1. Вектор Норма
2. Вектор L1 Норма
3. Вектор L2 Норма
4. Вектор Макс Норм

Видео:Лекция №2.2 НормыСкачать

Вектор Норма

Вычисление размера или длины вектора часто требуется либо непосредственно, либо как часть более широкой операции над вектором или векторной матрицей.

Длина вектора называется векторной нормой или величиной вектора.

Длина вектора представляет собой неотрицательное число, которое описывает экстент вектора в пространстве, и иногда его называют величиной или нормой вектора.

Длина вектора всегда является положительным числом, за исключением вектора со всеми нулевыми значениями. Он рассчитывается с использованием некоторой меры, которая суммирует расстояние вектора от начала векторного пространства. Например, источником векторного пространства для вектора с 3 элементами является (0, 0, 0).

Обозначения используются для представления векторной нормы в более широких вычислениях, а тип вычисления векторной нормы почти всегда имеет свои собственные уникальные обозначения.

Мы рассмотрим несколько общих вычислений векторной нормы, используемых в машинном обучении.

Видео:Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Вектор L1 Норма

Длина вектора может быть вычислена с использованием нормы L1, где 1 — верхний индекс L, например, L ^ 1.

Обозначения для нормы L1 вектора: || v || 1, где 1 — индекс. Таким образом, эту длину иногда называют нормой такси или нормой Манхэттена.

Норма L1 рассчитывается как сумма абсолютных значений вектора, где абсолютное значение скаляра использует обозначение | a1 |. По сути, норма — это вычисление манхэттенского расстояния от начала векторного пространства.

Норма L1 вектора может быть вычислена в NumPy с помощью функции norm () с параметром для указания порядка нормы, в данном случае 1.

Сначала определяется вектор 1 × 3, затем вычисляется норма вектора L1.

При выполнении примера сначала печатается определенный вектор, а затем норма L1 вектора.

Норма L1 часто используется при подборе алгоритмов машинного обучения в качестве метода регуляризации, например метод, позволяющий сохранять коэффициенты модели малыми, и, в свою очередь, модель менее сложной.

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Вектор L2 Норма

Длина вектора может быть вычислена с использованием нормы L2, где 2 — верхний индекс L, например, L ^ 2.

Обозначения для L2-нормы вектора: || v || 2, где 2 — индекс.

Норма L2 вычисляет расстояние векторной координаты от начала векторного пространства. Как таковая, она также известна как евклидова норма, поскольку она рассчитывается как евклидово расстояние от начала координат. Результатом является положительное значение расстояния.

Норма L2 рассчитывается как квадратный корень из суммы квадратов векторных значений.

Норму L2 вектора можно рассчитать в NumPy с помощью функции norm () с параметрами по умолчанию.

Сначала определяется вектор 1 × 3, затем вычисляется норма вектора L2.

При выполнении примера сначала печатается определенный вектор, а затем норма L2 вектора.

Как и норма L1, норма L2 часто используется при подборе алгоритмов машинного обучения в качестве метода регуляризации, например метод, позволяющий сохранять коэффициенты модели малыми и, в свою очередь, модель менее сложной.

Безусловно, норма L2 чаще используется, чем другие векторные нормы в машинном обучении.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Вектор Макс Норм

Длина вектора может быть рассчитана с использованием максимальной нормы, также называемой максимальной нормой.

Максимальная норма вектора называется L ^ inf, где inf — верхний индекс и может быть представлен символом бесконечности. Обозначения для максимальной нормы: || x || inf, где inf — индекс.

Максимальная норма вычисляется как возвращающая максимальное значение вектора, отсюда и название.

Максимальная норма вектора может быть вычислена в NumPy с помощью функции norm () с параметром порядка, установленным в inf.

Сначала определяется вектор 1 × 3, затем вычисляется максимальная норма вектора.

При запуске примера сначала печатается определенный вектор, а затем максимальная норма вектора

Максимальная норма также используется в качестве регуляризации в машинном обучении, например, в весах нейронных сетей, называемой максимальной нормализацией.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Создайте 5 примеров, используя каждую операцию, используя ваши собственные данные.
• Реализуйте каждую матричную операцию вручную для матриц, определенных как списки списков.
• Найдите документы по машинному обучению и найдите 1 пример каждой используемой операции.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Видео:Длина вектора через координаты. 9 класс.Скачать

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Введение в линейную алгебру, 2016
• Глава 2, Линейная алгебра,Глубокое обучение, 2016

статьи

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Резюме

В этом уроке вы обнаружили различные способы вычисления длины или величины вектора, называемые векторной нормой.

В частности, вы узнали:

• Норма L1, которая рассчитывается как сумма абсолютных значений вектора.
• Норма L2, которая рассчитывается как квадратный корень из суммы квадратов векторных значений.
• Максимальная норма, которая рассчитывается как максимальные значения вектора.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

Видео:Как выражать вектор? Как решать задачу с вектором? | TutorOnlineСкачать

Норма вектора в Python – шаги для расчета

Норма вектора относится к длине или величине вектора. Существуют разные способы рассчитать длину. Норма вектора является

• Автор записи

Автор: Pankaj Kumar
Дата записи

Норма вектора относится к длине или величине вектора. Существуют разные способы рассчитать длину. Норма вектора – неотрицательное значение. В этом руководстве мы узнаем, как рассчитать различные типы норм вектора.

Норма вектора x обозначается как: ‖ х ‖

Норма вектора – это мера ее расстояния от происхождения в векторном пространстве.

Для расчета нормы вы можете либо использовать Numpy или Scipy. Оба предлагают аналогичную функцию для расчета нормы.

В этом руководстве мы рассмотрим два типа норм, которые наиболее распространены в области машинного обучения.

Видео:Как проверить фазировку высоковольтного кабеля "на горячую" ? #энерголикбез #секретСкачать

Как рассчитать норму L1 вектора?

Н1 норм вектора также известен как Манхэттен Расстояние или Такси Норма Отказ Обозначение для л 1 Норма вектора x – ‖ х ‖ 1 Отказ

Чтобы рассчитать норму, вам нужно взять Сумма абсолютных векторных значений.

Давайте возьмем пример, чтобы понять это:

Для массива выше, L 1 Норма будет:

Давайте возьмем еще один пример:

L . 1 Норма этого массива:

L . 1 Норма для обоих векторов такая же, как мы рассмотрим абсолютные значения при вычислении его.

Реализация Python норм L1

Посмотрим, как мы можем рассчитать l 1 Норма вектора в Python.

Использование Numpy

Код Python для расчета l 1 Норма, используя Numpy выглядит следующим образом:

Давайте попробуем вычислить его для массива с отрицательными записями в нашем примере выше.

Использование Scipy

Для расчета l 1 Использование Scipy не сильно отличается от реализации выше.

Код для такого же есть:

Код точно похоже на Numpy.

Видео:Векторы для начинающих. Коллинеарные векторы. Как найти длину вектора? Нулевой векторСкачать

Как рассчитать норму L2 вектора?

Обозначение для L 2 Норма вектора x – ‖ х ‖ 2 Отказ

Для расчета l 2 Норма вектора, возьмите квадратный корень из суммы квадратных векторных значений.

Другое имя для л 2 Норма вектора – это Евклидово расстояние. Это часто используется для расчета ошибки в моделях машинного обучения.

Ошибка средневековой квадратной коренности является евклидое расстояние между фактическим выходом модели и ожидаемым выходом.

Целью модели обучения машины является снижение этой ошибки.

Давайте рассмотрим пример, чтобы понять это.

L . 2 Норма для вышеизложенного является:

Л 2 Норма всегда является положительным количеством, поскольку мы докладываем значения, прежде чем добавлять их.

Реализация Python

Реализация Python выглядит следующим образом:

Здесь мы можем увидеть это по умолчанию Норма метода Возвращает L 2 норма.

Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Заключение

Это руководство было о расчете L 1 и л 2 Нормы в Python. Мы использовали Numpy и Scipy для расчета двух норм. Надеюсь, вы веселились с нами!

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Вычислить норму вектора в l1

Пример 1. Вычисление норм вектора и матрицы.

Даны вектор b = и матрица A = . Вычислить нормы вектора и матрицы.

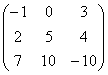
Вычислим нормы вектора: , , .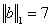

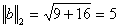
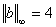
Соответствующие нормы матрицы: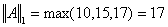
, , .

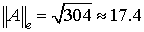
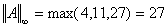
Пример 3. Оценка числа обусловленности и эксперимент.

A =

1-й шаг. Вычислим масштабирующие множители 1-го шага

, , .

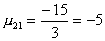
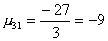
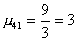
и выполним преобразование матрицы:

2-ой шаг. Вычислим масштабирующие множители 2-го шага

и .

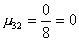
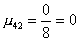
2-ой шаг не изменяет матрицы. A2 = A1.

3-й шаг. Вычислим масштабирующие множители 3-го шага

.

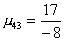
и выполним преобразование матрицы: A3 =

В результате получим матрицу U.

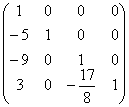
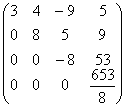
Таким образом, L = , U = .

Пример 5. Решение системы с помощью LU — разложения матрицы.

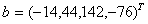
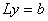
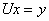
Решим систему уравнений Ax = b с матрицей A, рассмотренной в примере 4 и вектором . После разложения матрицы на множители, решение системы сводится к последовательному решению систем с треугольными матрицами: и .

Легко проверить, что решением 1-ой системы является вектор ,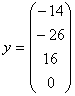
а решением 2-ой системы является вектор .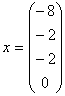

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

💡 Видео

Единичный векторСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

МОДУЛЬ ВЕКТОРА длина вектора 10 и 11 классСкачать

1. Векторы и параллелограмм задачи №1Скачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Координаты вектора. 9 класс.Скачать