| Координаты треугольника |
| Координаты точки |
| Вы ввели следующие координаты многоугольника |
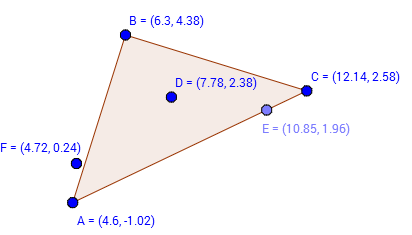
Определение, принадлежит ли произвольная точка какому либо треугольнику (находится ли она внутри треугольника, на самом деле очень важная задача. Для нас она важна в контексте разбиения многоугольника на треугольники. Решение этой промежуточной задачи, позволит нам определять координаты центра тяжести многоугольника. Итак, существует достаточно много вариантов определения принадлежности точки треугольнику. Могу порекомендовать ссылку. Написано достаточно подробно и рассмотрены практически все варианты. Мы в своей реализации будем придерживаться следующего алгоритма Пусть у нас есть треугольник Высчитаем значение трех нижеуказанных выражений где x0,y0 — координаты произвольной точки Если все три значения одинакового знака, то точка внутри треугольника, если значение равно нулю, значит точка лежит на стороне треугольника В ином случае (если значения различные по знаку) , точка вне треугольника. Теперь проверим наше предположение Точка лежит внутри треугольника так как результат трех вычислений одинаков по знаку ( все они отрицательные) В этом случае точка F лежит вне треугольника, так как знаки результирующих вычислений различны. Хотелось бы заметить, что в случае точки Е наш бот, скажет что точка также находится внутри треугольника, хотя и находится на стороне треугольника( или как вариант в одной из вершин) . Это как уже было сказано связано с использованием этого бота, для расчета центра тяжести многоугольников. Содержание
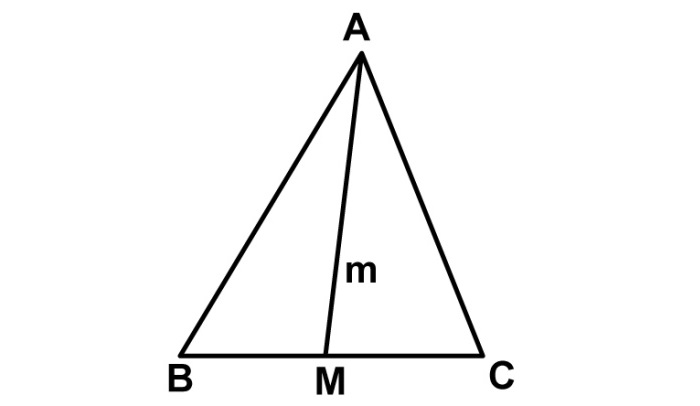
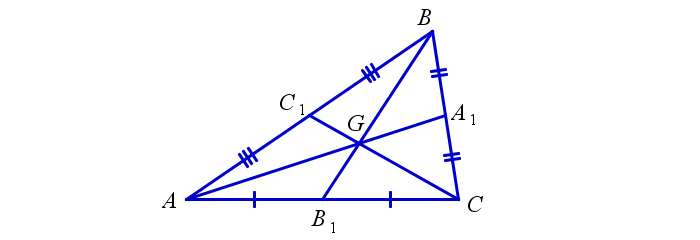
Видео:Замечательные точки треуг-ка. 8 класс.Скачать  Как определить лежит ли точка внутри треугольника или снаружи.Калькулятор поможет определить находится ли заданная точка внутри заданного треугольника. Точка и треугольник задаются декартовыми координатами на плоскости. Детально описан алгоритм вычисления. Этот калькулятор определит где находится заданная точка внутри 2-мерного треугольника или вовне. Калькулятор использует простой алгоритм, основанный на свойствах векторного произведения. Описание этого алгоритма можно найти сразу за калькулятором. Точка в треугольникеВекторное произведение ( z — координата )Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать  Точка внутри треугольника. Описание алгоритма.Векторное произведение векторов a и b, заданного декартовыми координатами в пространстве для 3-х мерного правого ортонормального базиса можно выразить так: Это важное свойство мы будем использовать для решения нашей задачи. Для того чтобы определить лежит ли точка P внутри треугольника ABC мы вычислим 3 векторных произведения: ABxAP, BCxBP and CAxCP. Так как наш треугольник и точка в 2-мерном пространстве на плоскости, третья координата z для трехмерного пространства равна нулю. Согласно формуле [1] мы можем не вычислять координаты x и y для векторного произведения, если координата z векторов-множителей равна нулю — координаты x и y результата в этом случае всегда равны нулю (результирующий псевдо-вектор перпендикулярен плоскости треугольника). Знак результата произведения для оставшейся координаты (z) зависит от относительного положения умножаемых векторов. Если первый вектор (в нашем случае это сторона треугольника) находится правее второго вектора (вектор из вершины в точку P), то координата z результата будет положительна, если первый вектор будет левее второго — отрицательна, и в противном случае, если оба вектора идут в одном и том же направлении, результат будет равен нулю. Видео:Где находится точка в треугольнике заданном координатами вершин, внутри или вне треугольника.Скачать  Ззамечательные точки треугольника — свойства, применение и примеры решенияЗамечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто. Итак, какие же четыре точки называются замечательными? Перечислим их: точку пересечения медиан треугольника; точку пересечения биссектрис треугольника; точку пересечения высот треугольника; точку пересечения серединных перпендикуляров сторон треугольника. Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке. Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки. Теперь рассмотрим основные положения, связанные с замечательными точками треугольника. Видео:8. Медиана треугольника и её свойства.Скачать  Точка пересечения медиан треугольникаИз курса геометрии известно определение медианы треугольника. На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС. Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан. Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С. На отрезке АВ отметьте центр С1, на стороне ВС центр А1, на АС центр В1. Проведите 3 медианы из вершин. Из угла А – медиана АА1,из угла В — медиана ВВ1, из угла С — медиана СС1. Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством). Изучим следующее свойство точки пересечения трёх медиан треугольника. Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка: Видео:Точка пересечения медиан в треугольникеСкачать  Точка пересечения биссектрис треугольникаПрежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её. 🌟 ВидеоУрок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать  Геометрия 7.Треугольники урок 6. Высота треугольника. Определение, свойства, точки пересечения высотСкачать  Окружность вписанная в треугольник и описанная около треугольника.Скачать  8 класс, 37 урок, Теорема о пересечении высот треугольникаСкачать  Высота, биссектриса, медиана. 7 класс.Скачать  Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать  8 класс, 36 урок, Свойства серединного перпендикуляра к отрезкуСкачать  Вписанные и описанные окружности. Вебинар | МатематикаСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать  7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать  8 класс, 35 урок, Свойства биссектрисы углаСкачать  четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать  Четыре замечательные точки треугольникаСкачать  Средняя линия треугольника и трапеции. 8 класс.Скачать  |

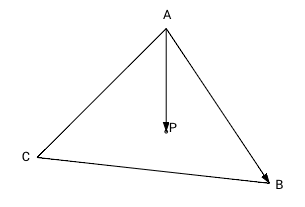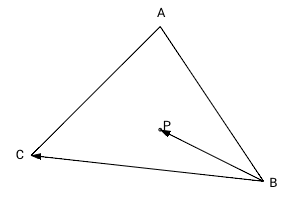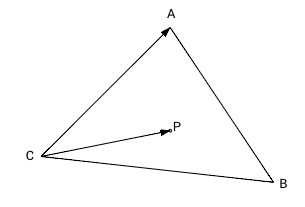 Попарное векторное произведение векторов-сторон треугольника и вектора из вершины в точку
Попарное векторное произведение векторов-сторон треугольника и вектора из вершины в точку