Всегда ли через две параллельные прямые можно провести плоскость а через две

В данном материале мы расскажем, как правильно вычислить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые. Начнем с формулировки основного принципа, а потом, как всегда, разберем несколько задач, где можно применить этот принцип на практике.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Как найти уравнение плоскости, проходящей через пересекающиеся прямые?

Для того чтобы вывести это уравнение, нам понадобится вспомнить одну теорему. Она звучит так:

Через две пересекающиеся прямые может проходить только одна плоскость.

Доказательство этого утверждения основано на двух аксиомах:

1. через три точки с разными координатами, которые не лежат на одной прямой, проходит только одна плоскость;
2. если у нас есть две точки прямой с разными координатами, расположенные в некоторой плоскости, то все точки этой прямой находятся в этой плоскости.

В итоге мы можем утверждать, что с помощью указания двух пересекающихся прямых мы можем задать определенную плоскость в трехмерном пространстве.

Далее нам нужно доказать, что плоскость, которая проходит через две определенные прямые, совпадет с той, что проходит через три заданные точки, две из которых находятся на тех самых прямых.

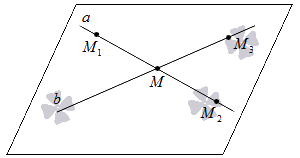
Допустим, у нас есть две прямые a и b с пересечением в некой точке M . Теперь расположим на первой прямой две точки М 1 и М 2 . У них должны быть разные координаты, но при этом одна из них может совпадать с точкой пересечения. На второй прямой отметим точку М 3 (но она совпадать с точкой M не должна). Теперь нам надо показать, что плоскость, проходящая через М 1 М 2 М 3 , – это та же самая плоскость, что проходит через пересекающиеся прямые a и b .

Посмотрим на схему:

Поскольку мы имеем точки прямой a , которые находятся в плоскости М 1 М 2 М 3 ( М 1 и М 2 ), то, используя аксиому, которую мы приводили выше, можно утверждать, что все точки этой прямой находятся в данной плоскости. Все точки прямой b тоже будут находиться в ней, поскольку там расположены две несовпадающие точки данной прямой ( М и М 3 ). Таким образом, мы доказали, что плоскости, в которых лежат данные прямые, совпадают.

Теперь перейдем непосредственно к формулировке уравнения плоскости, которая проходит через пересекающиеся прямые. Возьмем a и b , которые заданы в прямоугольной системе координат O x y z в трехмерном пространстве и являются пересекающимися. Напишем уравнение плоскости, которая проходит через эти прямые.

Все решение можно свести к нахождению уже изученного уравнения плоскости, проходящей через три точки. Сначала нам надо найти координаты двух точек M 1 и M 2 , которые расположены на пересекающихся прямых, и точки M 3 , которая находится на другой прямой и не является точкой их пересечения. Для этого можно использовать разные способы. Так, мы можем составить параметрические уравнения для первой прямой в пространстве. В итоге получим:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Отсюда можно вывести координаты x 1 , y 1 , z 1 точки M 1 , если λ = 0 . Для М 2 эти данные можно вычислить, если придать параметру любое действительное значение, отличное от нуля, например, единицу.

Далее мы можем составить такие же параметрические уравнения для второй прямой и, используя некоторое значение параметра, высчитать координаты М 3 . Важно проверить, чтобы она не лежала в точке пересечения прямых и вообще не находилась на прямой a .

Итак, мы нашли координаты всех нужных точек – М 1 , М 2 и М 3 . Переходим к написанию уравнения плоскости, которая через них проходит. Запишем:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0

Теперь найдем определитель матрицы x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 и получим общее уравнение для нужной нам плоскости, которая будет проходит через две заданные прямые a и b .

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

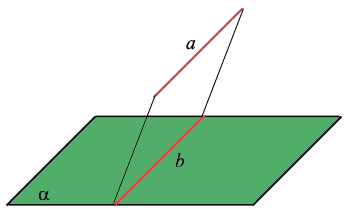
Как найти уравнение плоскости, проходящей через параллельные прямые?

Для этого нам понадобится вспомнить теорему, которая формулируется так:

Через две параллельные прямые проходит только одна плоскость.

Ее можно доказать, используя аксиому о единственной плоскости, которая проходит через три точки, а также утверждение о двух параллельных прямых (если одна из параллельных прямых пресекает некоторую плоскость, то это же делает и другая).

Итак, возможно задать плоскость в пространстве, если указать две параллельные прямые, которые в ней находятся.

Очевиден тот факт, что плоскость, которая проходит через 2 параллельные прямые и плоскость, которая проходит через три точки, две из которой лежат на одной из этих прямых, будут совпадать.

После этого мы можем найти уравнение плоскости, проходящей через две заданные параллельные прямые.

У нас есть прямоугольная система координат в трехмерном пространстве, которая обозначается O x y z . Составим уравнение плоскости, которая проходит через параллельные прямые a и b .

Сводим задачу опять же к нахождению уравнения для плоскости с тремя точками. В самом деле, можно определить, какие точно координаты будут иметь М 1 и М 2 , лежащие на одной из параллельных прямых, и М 3 , расположенная на другой прямой. После этого просто запишем нужное нам уравнение для плоскости, проходящей через три точки M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0

Это и есть нужное нам уравнение плоскости, проходящей через заданные параллельные прямые.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Примеры задач на нахождение подобных уравнений

Таким образом, для того чтобы составить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые, требуется вычислить координаты трех точек, которые расположены на этих прямых (две точки на одной прямой и третья на другой). Посмотрим, как это принцип реализуется на практике.

У нас задана прямоугольная система координат в трехмерном пространстве. Расположенная в ней прямая a проходит через точку M 1 ( — 3 , 1 , — 4 ) и пересекает координатную прямую O y в точке M 2 ( 0 , 5 , 0 ) . Составьте уравнение плоскости, которая будет проходить через пересекающиеся a и O y .

Решение

Изначально у нас заданы координаты двух точек, которые расположены на исходной прямой. Для составления уравнения нам нужна третья. Возьмем точку начала координат O ( 0 , 0 , 0 ) . Она расположена на O y и не совпадает с координатами двух точек, которые были заданы в условии. Та плоскость, что будет проходить через них, и есть та, для которой нам надо вывести уравнение. Запишем его в координатном виде:

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 0 y — 0 z — 0 — 3 — 0 1 — 0 — 4 — 0 0 — 0 5 — 0 0 — 0 = 0 ⇔ ⇔ x y z — 3 1 — 4 0 5 0 = 0 ⇔ 20 x — 15 z = 0 ⇔ 4 x — 3 z = 0

Ответ: 4 x — 3 z = 0 .

Возьмем более сложный пример, где координаты нужных точек не будут столь очевидными.

У нас есть две пересекающиеся прямые a и b , которые заданы с помощью уравнений.

x — 7 4 = y — 7 5 = z + 5 — 6 x — 3 1 = y — 2 — 3 = z — 1 5

Составьте уравнение плоскости, которая проходит через них.

Решение

Начнем с вычисления координат трех необходимых точек. Две из них расположены на прямой a , третья – на b .

Прямая в условии задана с помощью канонических уравнений в пространстве вида x — 7 4 = y — 7 5 = z + 5 — 6 , следовательно, она будет проходить через точку x — 7 4 = y — 7 5 = z + 5 — 6 .

Для вычисления координат второй точки нам надо записать параметрическое уравнение:

x — 7 4 = y — 7 5 = z + 5 — 6 ⇔ x = 7 + 4 · λ y = 7 + 5 · λ z = — 5 — 6 · λ

Если мы примем λ = 1 , то сможем подсчитать координаты второй точки:

x = 7 + 4 · λ y = 7 + 5 · λ z = — 5 — 6 · λ ⇔ x = 11 y = 12 z = — 11

Мы получили, что M 2 ( 11 , 12 , — 11 ) .

Понятно, что прямая, заданная с помощью уравнения x — 3 1 = y — 2 — 3 = z — 1 5 , будет проходить через точку M 3 ( 3 , 2 , 1 ) . Перед вычислениями надо проверить, не лежит ли она в точке пересечения прямых. Для этого надо подставить ее координаты во второе уравнение:

3 — 7 4 = 2 — 7 5 = 1 + 5 — 6 ⇔ — 1 ≡ — 1 ≡ — 1

Мы видим, что канонические уравнения прямой свелись к тождествам. Тогда наша третья точка лежит именно в месте пересечения прямых, значит, нам надо взять еще одну, которая будет находится на прямой b . Для этого также запишем параметрические уравнения:

x — 3 1 = y — 2 — 3 = z — 1 5 ⇔ x = 3 + μ y = 2 — 3 · μ z = 1 + 5 · μ

Высчитаем нужные координаты, приняв μ = 1 .

x = 3 + 1 y = 2 — 3 · 1 z = 1 + 5 · 1 ⇔ x = 4 y = — 1 z = 6 ⇔ M 3 ( 4 , — 1 , 6 )

Далее мы можем переходить непосредственно у формулированию уравнения нужной нам плоскости, которая будет проходить через M 1 ( 7 , 7 , — 5 ) , M 2 ( 11 , 12 , — 11 ) , M 3 ( 4 , — 1 , 6 ) :

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 7 y — 7 z — ( — 5 ) 11 — 7 12 — 7 — 11 — ( — 5 ) 4 — 7 — 1 — 7 6 — ( — 5 ) = 0 ⇔ ⇔ x — 7 y — 7 z + 5 4 5 — 6 — 3 — 8 11 = 0 ⇔ 7 x — 26 y — 17 z + 48 = 0

Ответ: 7 x — 26 y — 17 z + 48 = 0 .

Очевидно, что процесс вычисления координат нужных нам точек занимает больше всего времени при решении подобных задач.

Нам осталось разобрать пример плоскости, которая проходит через две прямые, являющиеся параллельными.

Составьте уравнение плоскости, которая проходит через две параллельные прямые. Они выражены с помощью уравнений x = 2 · λ y = 1 + λ z = — 1 — λ и x — 3 2 = y 1 = z + 5 — 1 .

Решение

Вычисляем координаты двух нужных точек по параметрическим уравнениям, приняв λ = 0 и λ = 1 .

λ = 0 : x = 2 · 0 y = 1 + 0 z = — 1 — 0 ⇔ x = 0 y = 1 z = — 1 ⇔ M 1 ( 0 , 1 , — 1 ) λ = 1 : x = 2 · 1 y = 1 + 1 z = — 1 — 1 ⇔ x = 2 y = 2 z = — 2 ⇔ M 2 ( 2 , 2 , — 2 )

У нас получается, что прямая x — 3 2 = y 1 = z + 5 — 1 будет проходить через точку M 3 ( 3 , 0 , — 5 ) .

Переходим к уравнению плоскости для трех точек М 1 , М 2 и М 3 :

x — x 1 y — y 1 z — z 1 x 2 — x 1 y 2 — y 1 z 2 — z 1 x 3 — x 1 y 3 — y 1 z 3 — z 1 = 0 ⇔ x — 0 y — 1 z — ( — 1 ) 2 — 0 2 — 1 — 2 — ( — 1 ) 3 — 0 0 — 1 — 5 — ( — 1 ) = 0 ⇔ ⇔ x y — 1 z + 1 2 1 — 1 3 — 1 — 4 = 0 ⇔ — 5 x + 5 y — 5 z — 10 = 0 ⇔ x — y — z + 2 = 0

Ответ: x — y — z + 2 = 0 .

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Урок 1 Предмет стереометрии. Аксиомы стереометрии (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

По рисунку назовите пары скрещивающихся ребер; пары параллельных ребер.

Итак, алгоритм распознавания взаимного расположения двух прямых в пространстве.

II. Решение задач.

1. Всегда ли две непересекающиеся прямые в пространстве параллельны? (Устно.)

2. Какие две прямые называются параллельными? (Устно.)

3. Дано а || b. Докажите, что все прямые, пересекающие данные, лежат в одной плоскости.

4. Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой? (п. 4).

Домашнее задание: теория (п. 4), №№ 16, 89. Постройте сечение многогранника плоскостью (MNK).

Урок 2
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ.
ПАРАЛЛЕЛЬНОСТЬ ТРЕХ ПРЯМЫХ

Цели: доказать лемму о пересечении плоскости параллельными прямыми, теорему о трех параллельных прямых; показать их применение при решении задач.

I. Проверка домашнего задания (у доски).

II. Устная работа.

1. АВСDА1В1С1D1 – куб. Все грани – квадраты. Установите взаимное расположение прямых.

2. Какие прямые называются параллельными? Скрещивающимися?

III. Объяснение нового материала построить в соответствии с п. 5 учебника.

IV. Решение задач.

Дано: DM = MB, DN = NC,
AQ = QC, AP = PB, AD = 12,
BC = 14.

1.

2.

3. По определению MNQP – параллелограмм.

4. PQ = 7, PM = 6 PMNQP = 2 (7 + 6) = 26.

(Докажите устно, несколькими способами, что MNQP – параллелограмм. Используя признаки параллелограмма.)

Дано: АBCD – параллелограмм,

АВ б = K, ВС б = F.

Доказать, что AD б, DC б.

1.

2. Аналогично, AD б.

Дано: ABCD – трапеция, MN – средняя линия, MN б.

Доказать: пересекают ли ВС и АD плоскость б?

Пусть ВС б, тогда

Получили противоречие, так как MN б. Следовательно, ВС б.

Аналогично АD б.

Дано: А б, СС1 || ВВ1,
АС = СВ, ВВ1 = 7.

I. Необходимо доказать, что точки А, С1 и В1 лежат на одной прямой.

2. в б = АВ1. Докажем, что С1 АВ1.

3. Пусть С1 АВ1, тогда СС1 в = С.

Противоречие условию, ВВ1 в.

Следовательно, С1 АВ1. (Проведите различные доказательства, проводя плоскость в через А и СС1, через СС1 и ВВ1).

II. СС1 – средняя линия Δ АВВ1 ⇒ СС1 = 3,5.

Домашнее задание: теория (п. 4 – 5), №№ 18 (б), 21, 88. Построить сечение многогранника плоскостью (MNK).

Урок 3
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ В ПРОСТРАНСТВЕ.
ПАРАЛЛЕЛЬНОСТЬ ТРЕХ ПРЯМЫХ

Цель: закрепить навык применения теорем о параллельных прямых при решении задач.

I. Проверка домашнего задания.

II. Устная работа.

1. Какие прямые в пространстве называются параллельными?

2. Всегда ли через две параллельные прямые можно провести плоскость? А через две непересекающиеся прямые?

3. В пространстве даны n параллельных между собой прямых. Известно, что никакие три из них не лежат в одной плоскости. Сколько различных плоскостей можно провести через эти прямые?

4. Сформулируйте лемму о пересечении плоскости параллельными прямыми.

5. Отрезок, соединяющий середины двух сторон треугольника, лежит в плоскости б. Пересекает ли третья сторона эту плоскость?

6. Сформулируйте теорему о трех параллельных прямых.

7. Дано: АА1 || СС1,

Доказать, что В1С1 = ВС.

III. Решение задач.

Дано: AB б, AC = CB,

I. Докажем, что точки A1, C1 и B1 лежат на одной прямой.

1. (AA1, BB1) = в. в б = A1B1. Докажем, что C1 A1B1.

2. Пусть С1 А1В1, тогда CC1 в = C.

Полученное противоречие опровергает наше предположение.

Следовательно, С1 А1В1.

3. СС1 – средняя линия трапеции ⇒ CC1 == 6.

Дано: AB б = D; AC = CB; АА1 || СС1 || ВВ1; АА1 = 5; ВВ1 = 7.

I. Доказать, что точки А1, С1, D и В1 лежат на одной прямой.

СС1 – отрезок, соединяющий середины диагоналей трапеции.

СС1 == 1.

СС1 = C1K – CK = BB1 – AA1 = 3,5 – 2,5 = 1.

Дано: АВСD – параллелограмм,

АА1 || ВВ1 || CC1 || DD1,

АА1 = 2, ВВ1 = 3, СС1 = 8.

Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С – параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1. Найдите длину отрезка ВВ1, если:

Видео:Параллельность прямых. 10 класс.Скачать

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

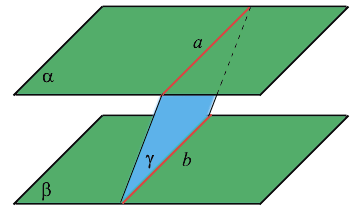
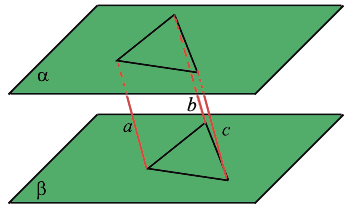
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

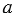
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

.

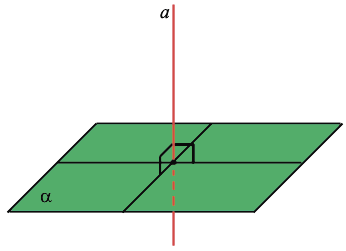
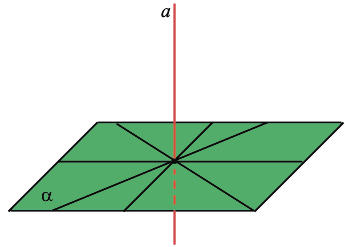
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

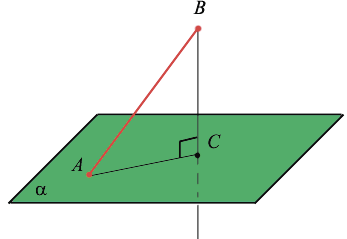
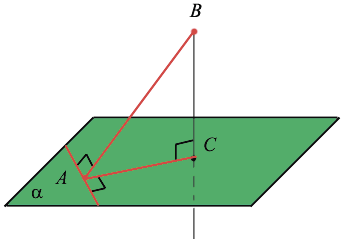
Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

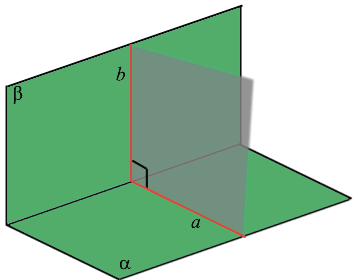
Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

📸 Видео

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

10 класс, 3 урок, Некоторые следствия из аксиомСкачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Параллельность прямых, плоскостей, прямой и плоскости | Математика ЕГЭ для 10 класса | УмскулСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Параллельность прямой к плоскостиСкачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ перпендикулярные к плоскости 10 классСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

10 класс, 10 урок, Параллельные плоскостиСкачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

№51. Докажите, что плоскости α и β параллельны, если две пересекающиеся прямые mСкачать

ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать

10 класс, 2 урок, Аксиомы стереометрииСкачать