Высоту пирамиды построенной на векторах

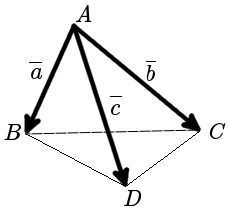
Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x₂ – x₁; Y = y₂ – y₁; Z = z₂ – z₁
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) .
Длину вектора находим по формуле:

Пример №2 . В тетраэдре ABCD вычислить:

1. объем тетраэдра ABCD;
2. высоту тетраэдра, опущенную из вершины D на грань ABC.

A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1)

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Ответ

Проверено экспертом

Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .

Находим векторы АВ, АС и АД.

Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.

Определяем векторное произведение АВ х АС.

-6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0).

Далее находим смешанное произведение (АВ х АС) х АД.

(АВ х АС) = (-5; -10; 0),

(АВ х АС) х АД = 30 + 10 + 0 = 40.

Объем пирамиды равен (1/6) этого произведения:

V = (1/6)*40 = (20/3) куб.ед.

Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).

Площадь основания АВС равна половине модуля векторного произведения АВ х АС.

S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.

h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах. Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал. Видео:Площадь треугольника, построенного на векторахСкачать Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах Выберите каким образом задается пирамида (тетраэдр): Введите значения векторов: Введите координаты вершин пирамиды: Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре. Видео:Решение, найти объем пирамиды, построенной на векторах a, b, c пример 15 Высшая математикаСкачать Теория. Объем пирамиды (объем тетраэдра) построенной на векторах Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду: V = 1 | a ·[ b × c ]| 6 Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики. 📹 Видео Решение, найдите объем пирамиды, построенной на векторах a, b, c пример 6Скачать §20 Нахождение объёма параллелипипедаСкачать Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать Найдите площадь параллелограмма, построенного на векторахСкачать Компланарность векторов. Объём пирамидыСкачать Решение, вычислить объем пирамиды, построенной на векторах a, b, c пример 12 Высшая математикаСкачать Решение, найдите объем пирамиды, построенной на векторах a, b, c пример 8Скачать Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать Площадь параллелограмма по векторамСкачать Смешанное произведение векторов. Объем треугольной пирамиды на векторахСкачать 18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать 18+ Математика без Ху!ни. Векторное произведение.Скачать Вычисляем высоту через координаты вершин 1Скачать Задача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать как найти площадь параллелограмма построенного на векторахСкачать Поделиться или сохранить к себе: Смотрите также Ящик с инструментами в векторе Якорь в векторе черно белый Який вектор колінеарний до будь якого вектора Як знайти точку в векторе Являются ли точки вершинами трапеции векторы Юрий бурлан тест на вектор Эффективность относится к вектору аудита исполнительному стратегическому Эмблема службы горючего вс рф в векторе