Все теоремы четырехугольника 8 класс

8 класс. Геометрия. Четырехугольники. Прямоугольник, ромб и квадрат.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

По­вто­ре­ние тео­рии и ре­ше­ние задач

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

1. Определение, виды и свойства трапеции

Ранее мы уже по­зна­ко­ми­лись с та­ки­ми ви­да­ми че­ты­рех­уголь­ни­ков, как па­рал­ле­ло­грамм и тра­пе­ция, и их част­ны­ми слу­ча­я­ми – пря­мо­уголь­ни­ком, ром­бом и квад­ра­том. Мы изу­чи­ли их ос­нов­ные свой­ства и при­зна­ки. Се­год­ня мы по­вто­рим и обоб­щим все по­лу­чен­ные нами зна­ния по этой теме.

По­вто­рим ос­нов­ной тео­ре­ти­че­ский ма­те­ри­ал.

Тра­пе­ция – это че­ты­рех­уголь­ник, у ко­то­ро­го две про­ти­во­по­лож­ные сто­ро­ны па­рал­лель­ны, а две дру­гие не па­рал­лель­ны (см. Рис. 1).

Вы­де­ля­ют два от­дель­ных типа тра­пе­ций: рав­но­бед­рен­ную и пря­мо­уголь­ную.

Рав­но­бед­рен­ная тра­пе­ция – это тра­пе­ция, в ко­то­рой бо­ко­вые сто­ро­ны равны (см. Рис. 2).

Рис. 2. Рав­но­бед­рен­ная тра­пе­ция

Пря­мо­уголь­ная тра­пе­ция – это тра­пе­ция, в ко­то­рой одна из бо­ко­вых сто­рон пер­пен­ди­ку­ляр­на ос­но­ва­нию (см. Рис. 3).

Рис. 3. Пря­мо­уголь­ная тра­пе­ция

От­дель­но стоит вспом­нить такой важ­ный эле­мент тра­пе­ции, как ее сред­няя линия.

Сред­няя линия тра­пе­ции – это от­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны бо­ко­вых сто­рон тра­пе­ции (см. Рис. 4).

Рис. 4. Сред­няя линия тра­пе­ции

Ос­нов­ные свой­ства сред­ней линии тра­пе­ции:

1. – па­рал­лель­на ос­но­ва­ни­ям тра­пе­ции;

2. – равна их по­лу­сум­ме.

Видео:ВСЯ ТЕОРИЯ по ГЕОМЕТРИИ ЗА 8 КЛАСС с примерамиСкачать

2. Определение, свойства и признаки параллелограмма

Па­рал­ле­ло­грамм – че­ты­рех­уголь­ник, у ко­то­ро­го каж­дые две про­ти­во­по­лож­ные сто­ро­ны па­рал­лель­ны (см. Рис. 5).

Рис. 5. Па­рал­ле­ло­грамм

Ос­нов­ные свой­ства па­рал­ле­ло­грам­ма:

Чтобы иметь воз­мож­ность при ре­ше­нии задач поль­зо­вать­ся ука­зан­ны­ми свой­ства­ми, нам необ­хо­ди­мо по­ни­мать, яв­ля­ет­ся ли ука­зан­ный че­ты­рех­уголь­ник па­рал­ле­ло­грам­мом или нет. Для этого необ­хо­ди­мо знать при­зна­ки па­рал­ле­ло­грам­ма.

Тео­ре­ма. Пер­вый при­знак па­рал­ле­ло­грам­ма. Если в че­ты­рех­уголь­ни­ке две про­ти­во­по­лож­ные сто­ро­ны равны и па­рал­лель­ны (см. Рис. 6), то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. па­рал­ле­ло­грамм.

Рис. 6. Пер­вый при­знак па­рал­ле­ло­грам­ма

Тео­ре­ма. Вто­рой при­знак па­рал­ле­ло­грам­ма. Если в че­ты­рех­уголь­ни­ке каж­дые две про­ти­во­по­лож­ные сто­ро­ны равны (см. Рис. 7), то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. па­рал­ле­ло­грамм.

Рис. 7. Вто­рой при­знак па­рал­ле­ло­грам­ма

Тео­ре­ма. Тре­тий при­знак па­рал­ле­ло­грам­ма. Если в че­ты­рех­уголь­ни­ке диа­го­на­ли точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам (см. Рис. 8), то этот че­ты­рех­уголь­ник – па­рал­ле­ло­грамм. па­рал­ле­ло­грамм.

Рис. 8. Тре­тий при­знак па­рал­ле­ло­грам­ма

Те­перь по­вто­рим част­ные слу­чаи па­рал­ле­ло­грам­ма.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

3. Определение, свойство и признак прямоугольника

Пря­мо­уголь­ни­ком на­зы­ва­ют па­рал­ле­ло­грамм, у ко­то­ро­го все углы пря­мые (см. Рис. 9).

Рис. 9. Пря­мо­уголь­ник

За­ме­ча­ние. Оче­вид­ным эк­ви­ва­лент­ным опре­де­ле­ни­ем пря­мо­уголь­ни­ка (ино­гда его име­ну­ют при­зна­ком пря­мо­уголь­ни­ка) можно на­звать сле­ду­ю­щее. Пря­мо­уголь­ник – это па­рал­ле­ло­грамм с одним углом . Это утвер­жде­ние прак­ти­че­ски оче­вид­но, и мы оста­вим его без до­ка­за­тель­ства, поль­зу­ясь далее как опре­де­ле­ни­ем.

Т.к. пря­мо­уголь­ник, как это видно из опре­де­ле­ния, яв­ля­ет­ся част­ным слу­ча­ем па­рал­ле­ло­грам­ма, то ему при­су­щи все ранее опи­сан­ные свой­ства па­рал­ле­ло­грам­ма, од­на­ко у него име­ют­ся и свои спе­ци­фи­че­ские свой­ства, ко­то­рые мы сей­час рас­смот­рим.

Тео­ре­ма. Свой­ство пря­мо­уголь­ни­ка. Диа­го­на­ли пря­мо­уголь­ни­ка равны (см. Рис. 10).

.

Рис. 10. Свой­ство пря­мо­уголь­ни­ка

Тео­ре­ма. При­знак пря­мо­уголь­ни­ка. Если в па­рал­ле­ло­грам­ме диа­го­на­ли равны, то этот па­рал­ле­ло­грамм – пря­мо­уголь­ник (см. Рис. 11).

Рис. 11. При­знак пря­мо­уголь­ни­ка

Видео:ЧЕТЫРЕХУГОЛЬНИКИ и их свойства+доказательство теорем/8 класс.Скачать

4. Определение и свойство ромба

Ромб – па­рал­ле­ло­грамм, у ко­то­ро­го все сто­ро­ны равны (см. Рис. 12).

За­ме­ча­ние. Для опре­де­ле­ния ромба до­ста­точ­но ука­зы­вать даже более ко­рот­кое утвер­жде­ние, что это па­рал­ле­ло­грамм, у ко­то­ро­го равны две смеж­ные сто­ро­ны .

Ромб об­ла­да­ет всеми свой­ства­ми па­рал­ле­ло­грам­ма, т.к. яв­ля­ет­ся его част­ным слу­ча­ем, но имеет и свое спе­ци­фи­че­ское свой­ство.

Тео­ре­ма. Свой­ство ромба. Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны и делят углы ромба по­по­лам (см. Рис. 13).

Рис. 13. Свой­ство ромба

Видео:Геометрия 8 класс за 1 час | Математика | УмскулСкачать

5. Определение и свойства квадрата

Квад­рат – 1) пря­мо­уголь­ник, у ко­то­ро­го сто­ро­ны равны; 2) ромб, у ко­то­ро­го углы пря­мые (см. Рис. 14). Ука­зан­ные опре­де­ле­ния эк­ви­ва­лент­ны и при­ме­ня­ют­ся в любой удоб­ной форме.

Квад­ра­ту при­су­щи свой­ства тех фигур, част­ным слу­ча­ем ко­то­рых он яв­ля­ет­ся (па­рал­ле­ло­грамм, пря­мо­уголь­ник, ромб). Пе­ре­чис­лим их.

Ос­нов­ные свой­ства квад­ра­та (см. Рис. 15):

1. Все углы пря­мые.

2. Диа­го­на­ли равны.

3. Диа­го­на­ли пер­пен­ди­ку­ляр­ны.

4. Точка пе­ре­се­че­ния делит диа­го­на­ли по­по­лам.

5. Диа­го­на­ли делят углы квад­ра­та по­по­лам.

Рис. 15. Свой­ства квад­ра­та

Видео:ЧЕТЫРЕХУГОЛЬНИК и его элементы. §1 геометрия 8 классСкачать

6. Задача на схожесть свойств трапеции и параллелограмма

Те­перь, когда мы пе­ре­чис­ли­ли и вспом­ни­ли ос­нов­ные свой­ства ос­нов­ных изу­чен­ных че­ты­рех­уголь­ни­ков, мы можем за­кре­пить эти зна­ния на при­ме­ре ре­ше­ния задач.

При­мер 1. (Обоб­щен­ная за­да­ча на тра­пе­цию и па­рал­ле­ло­грамм). Дана тра­пе­ция или па­рал­ле­ло­грамм (см. Рис. 16). бис­сек­три­сы углов при бо­ко­вой сто­роне тра­пе­ции (па­рал­ле­ло­грам­ма). Найти угол между бис­сек­три­са­ми .

Ре­ше­ние. Это при­мер за­да­чи, де­мон­стри­ру­ю­щий схо­жесть неко­то­рых свойств па­рал­ле­ло­грам­ма и тра­пе­ции, в нем не важно, какая кон­крет­но из этих двух фигур за­да­на. Изоб­ра­зим ри­су­нок.

– бис­сек­три­сы, они делят со­от­вет­ству­ю­щие углы по­по­лам, обо­зна­чим их и .

По свой­ству тра­пе­ции (па­рал­ле­ло­грам­ма) .

Рас­смот­рим : .

Ответ: .

Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

7. Теорема Фалеса и задача на ее применение

Вспом­ним фор­му­ли­ров­ку тео­ре­мы Фа­ле­са.

Тео­ре­ма Фа­ле­са. Если па­рал­лель­ные пря­мые, ко­то­рые пе­ре­се­ка­ют сто­ро­ны угла, от­се­ка­ют на одной его сто­роне рав­ные от­рез­ки, то они от­се­ка­ют рав­ные от­рез­ки и на дру­гой его сто­роне (см. Рис. 17).

Рис. 17. Тео­ре­ма Фа­ле­са

Рас­смот­рим за­да­чу на тра­пе­цию с при­ме­не­ни­ем тео­ре­мы Фа­ле­са.

При­мер 2. Бо­ко­вая сто­ро­на тра­пе­ции раз­де­ле­на на три рав­ные части, и из точек де­ле­ния про­ве­де­ны к дру­гой сто­роне от­рез­ки, па­рал­лель­ные ос­но­ва­ни­ям. Най­ди­те длину этих от­рез­ков, если ос­но­ва­ния тра­пе­ции равны 2 м и 5 м.

Ре­ше­ние. Изоб­ра­зим Рис. 18 со всеми эле­мен­та­ми, ко­то­рые при­го­дят­ся нам в про­цес­се ре­ше­ния. Из­вест­но, что . Найти длины .

Для того, чтобы вос­поль­зо­вать­ся тео­ре­мой Фа­ле­са от­но­си­тель­но угла , про­ве­дем пря­мые .

Сна­ча­ла рас­смот­рим па­рал­ле­ло­грамм , в нем по свой­ству .

Вер­нем­ся к про­ве­ден­ным па­рал­лель­ным пря­мым, по тео­ре­ме Фа­ле­са: . . По­сколь­ку от­ре­зок раз­де­лен на три рав­ные части, то .

Те­перь, если вни­ма­тель­но по­смот­реть на па­рал­ле­ло­грам­мы, об­ра­зо­ван­ные пе­ре­се­че­ни­я­ми линий с про­ве­ден­ны­ми нами пря­мы­ми , можно легко опре­де­лить длины от­рез­ков : , .

Ответ. .

При­мер 3. Ос­но­ва­ния тра­пе­ции от­но­сят­ся как 2:3. Сред­няя линия равна 5 м. Най­ди­те ос­но­ва­ния.

Ре­ше­ние. Изоб­ра­зим Рис. 19 и ука­жем, что нам дано: . Найти и .

По­сколь­ку из­вест­но, что , то вы­ра­зим ос­но­ва­ния тра­пе­ции через услов­ные части : . За­пи­шем свой­ство сред­ней линии тра­пе­ции:

.

Ответ. .

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

8. Разные задачи на четырехугольники

При­мер 4. Через дан­ную точку внут­ри угла про­ве­ди­те пря­мую, от­ре­зок ко­то­рой, за­клю­чен­ный внут­ри этого угла, де­лил­ся бы дан­ной точ­кой по­по­лам.

Ре­ше­ние. Внут­ри угла с вер­ши­ной дана точка . Изоб­ра­зим это на Рис. 20 со всеми эле­мен­та­ми, ко­то­рые по­на­до­бят­ся нам для ре­ше­ния за­да­чи.

От­ло­жим от­ре­зок из точки через точку так, чтобы , затем про­ве­дем от­рез­ки , по­лу­чим точки пе­ре­се­че­ния со сто­ро­на­ми угла и со­от­вет­ствен­но. Со­еди­ним эти точки пря­мой, она и будет ис­ко­мой. До­ка­жем это.

По­стро­ен­ная фи­гу­ра яв­ля­ет­ся па­рал­ле­ло­грам­мом, т.к. по по­стро­е­нию имеет па­рал­лель­ные про­ти­во­по­лож­ные сто­ро­ны, от­рез­ки яв­ля­ют­ся диа­го­на­ля­ми па­рал­ле­ло­грам­ма, сле­до­ва­тель­но, по его свой­ству точ­кой пе­ре­се­че­ния () де­лят­ся по­по­лам и , что и тре­бо­ва­лось по усло­вию за­да­чи.

Ответ. Ис­ко­мая пря­мая – .

При­мер 5. В пря­мо­уголь­ни­ке точка пе­ре­се­че­ния диа­го­на­лей от­сто­ит от мень­шей сто­ро­ны на 4 см даль­ше, чем от боль­шей сто­ро­ны. Пе­ри­метр пря­мо­уголь­ни­ка равен 56 см. Най­ди­те сто­ро­ны пря­мо­уголь­ни­ка.

Ре­ше­ние. Изоб­ра­зим Рис. 21.

Опу­стим из точки пе­ре­се­че­ния диа­го­на­лей пер­пен­ди­ку­ля­ры на сто­ро­ны, длины ко­то­рых и будут рас­сто­я­ни­я­ми от точки пе­ре­се­че­ния диа­го­на­лей до сто­рон пря­мо­уголь­ни­ка. Обо­зна­чим от­ре­зок , тогда по усло­вию . По­сколь­ку по­лу­ча­ем, что . Под­ста­вим это в фор­му­лу пе­ри­мет­ра пря­мо­уголь­ни­ка:

.

Ответ: .

Видео:Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

Все теоремы четырехугольника 8 класс

Четырехугольник — фигура, состоящая из четырех точек и четырех отрезков,последовательно их соединяющих; причем ни одна из трех данных точек не лежит на одной прямой, а отрезки, соединяющие их, не пересекаются.

Соседние вершины — вершины четырехугольника, являющиеся концами одной из его сторон.
Противолежащие вершины — несоседние вершины.
Соседние стороны — стороны выходящие из одной вершины. Противолежащие стороны — несоседние стороны.
Диагональ четырехугольника — отрезок, соединяющий противолежащие вершины четырехугольника.
Периметр четырехугольника — сумма длин всех сторон.
Выпуклый четырехугoльник — четырехугольник, лежащий в одной полуплоскости относительно прямой,содержащей его сторону.
Внешний угол четырехугольника — угол,смежный с углом четырехугольника.

Свойства углов и сторон четырехугольника

Свойства углов
1. Сумма углов четырехугольника равна 360°.
2. Сумма внешних углов четырехугольника, взятых по одному при каждой вершине, равна 360°.

Свойства сторон
1. Каждая сторона четырехугольника меньше суммы всех его других сторон.
2. Сумма диагоналей меньше его периметра.

Виды четырехугольников

Конспекты по четырехугольникам:

Это конспект по теме «Четырехугольники и его свойства». Выберите дальнейшие действия:

Видео:Четырехугольники. Вебинар | МатематикаСкачать

Геометрия. Урок 4. Четырехугольники

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение четырехугольника

• Выпуклые четырехугольники

• Параллелограмм

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

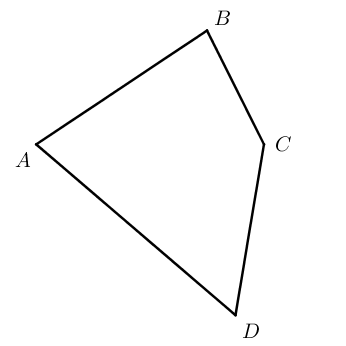
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

Видео:Все теоремы по геометрии за 8 классСкачать

Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

Видео:ВСЯ ГЕОМЕТРИЯ 8 КЛАСС ЗА 15 МИНУТ / АТАНАСЯН / К ОГЭСкачать

Параллелограмм

Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

• Противолежащие стороны равны.
• Противоположные углы равны.
• Диагонали точкой пересечения делятся пополам.
• Сумма углов, прилежащих к одной стороне, равна 180 ° .
• Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

Как произведение двух смежных (соседних) сторон на синус угла между ними.

Как полупроизведение диагоналей на синус угла между ними.

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

• Диагонали пересекаются под прямым углом.
• Диагонали являются биссектрисами углов, из которых выходят.
• Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

Как произведение стороны ромба на высоту ромба.

Как квадрат стороны ромба на синус угла между двумя сторонами.

Как полупроизведение диагоналей ромба.

Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Прямоугольник

Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .

Свойства прямоугольника:

• Диагонали прямоугольника равны.
• Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

Как произведение двух смежных (соседних) сторон прямоугольника.

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

Видео:Теорема Пифагора. 8 КЛАСС | Математика | TutorOnlineСкачать

Квадрат

Квадрат – прямоугольник, у которого все стороны равны.

Свойства квадрата:

• Сохраняет свойства ромба.
• Сохраняет свойства прямоугольника.

Площадь квадрата можно вычислить по двум формулам:

Как квадрат стороны.

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .

B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна 180 ° .

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

Площадь трапеции можно найти по двум формулам:

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

Прямоугольная трапеция – трапеция, у которой два угла прямые.

Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Свойство равнобокой трапеции: углы при основании равны

Видео:Математика| Геометрия 8 класса в одной задачеСкачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

📽️ Видео

Как быстро и легко выучить теорему по математике. На примере теоремы ПифагораСкачать

Прямоугольник. 8 класс.Скачать

8 класс, 7 урок, ПрямоугольникСкачать