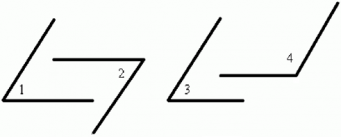Все пары углов при двух параллельных прямых и секущей

51. Планиметрия Читать 0 мин.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

51.65. Углы и параллельные прямые

Взаимное расположение прямых:

• Прямые пересекаются, у них есть одна общая точка.
• Прямые не пересекаются, у них нет общих точек. Такие прямые называются параллельными.

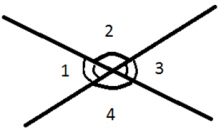
При пересечении двух прямых образуются вертикальные и смежные углы.

Вертикальные углы — равны.

Сумма смежных углов равна 180°.

Параллельные прямые

Прямые называются параллельными, если они не пересекаются, сколько бы их не продолжать.

О параллельных прямых:

• Если одна из пары параллельных прямых параллельна третьей прямой, то все прямые параллельны между собой.
• На плоскости через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
• Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.

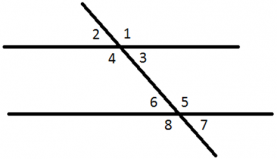
При пересечении двух параллельных прямых секущей образуются следующие углы:

• внутренние накрест лежащие (4 и 5, 3 и 6) — попарно равны;
• внешние накрест лежащие (1 и 8, 2 и 7) — попарно равны;
• соответственные (1 и 5, 2 и 6, 3 и 7, 4 и 8) — попарно равны;
• внутренние односторонние (3 и 5, 4 и 6) — сумма таких углов равна 180°;
• внешние односторонние (1 и 7, 2 и 8) — сумма таких углов равна 180°.

Часто для использования свойств углов, полученных при пересечении двух параллельных прямых секущей, необходимо применять дополнительные построения.

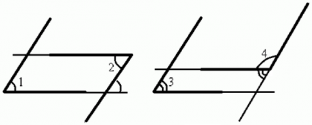
Пример: Даны углы с попарно параллельными сторонами. Что можно сказать об углах 1 и 2? Что можно сказать об углах 3 и 4?

Продолжим стороны углов до пересечения:

Получаем, что углы 1 и 2 равны, т. к. являются накрест лежащими при параллельных прямых.

Сумма углов 3 и 4 равна 180°, т. к. они являются односторонними при параллельных прямых.

Теорема Фалеса: При пересечении сторон угла параллельными прямыми стороны угла делятся на пропорциональные отрезки (образуются подобные треугольники).

Видео:Пары углов в геометрииСкачать

Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы

Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы и , и — тоже вертикальные.

Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.

Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть

Углы и (а также и , и , и ) называются соответственными.

Соответственные углы равны, то есть

Углы и (а также и , и , и ) называют накрест лежащими.

Накрест лежащие углы равны, то есть

Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.

Ты нашел то, что искал? Поделись с друзьями!

1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Напомним, что биссектриса угла — это луч, выходящий из вершины угла и делящий угол пополам.

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.

Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .

Периметр параллелограмма — это сумма всех его сторон, то есть

2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.

Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .

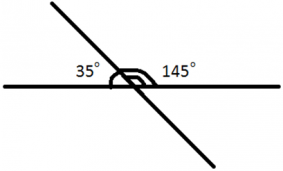
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на чертеж. По условию, , то есть .

Углы и — односторонние при параллельных прямых и секущей, следовательно,

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Геометрия. Урок 2. Углы

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Углы

Видео:Углы, образованные при пересечении двух прямых секущейСкачать

Понятие угла

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .

Величину угла измеряют в градусах. ∠ A O B = 24 ° .

Видео:УГЛЫ ПРИ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ И СЕКУЩЕЙСкачать

Виды углов:

Видео:Все виды углов при параллельных прямых и секущей #математика #огэ #огэматематика #семенСкачать

Биссектриса угла

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.

∠ A O D = ∠ B O D = ∠ A O B 2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .

Видео:№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Углы, образованные при пересечении двух прямых

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180 ° .

( 1 ) и ( 3 )
( 2 ) и ( 4 )

называются вертикальными .

По свойству вертикальных углов:

∠ C O D = ∠ A O B
∠ B O D = ∠ A O C

( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )

называются смежными .

По свойству смежных углов:

∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °

Видео:Углы, образованные параллельными прямыми и секущейСкачать

Углы, образованные при пересечении двух прямых секущей

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )

называются соответственными .
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

( 3 ) и ( 5 )
( 4 ) и ( 6 )

называются внутренними односторонними .
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

( 1 ) и ( 7 )
( 2 ) и ( 8 )

называются внешними односторонними .
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

( 3 ) и ( 6 )
( 4 ) и ( 5 )

называются внутренними накрест лежащими .
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

( 1 ) и ( 8 )
( 2 ) и ( 7 )

называются внешними накрест лежащими .
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180 ° .
• Сумма внешних односторонних углов равна 180 ° .

Видео:Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Сумма углов многоугольника

Сумма углов произвольного n -угольника вычисляется по формуле:

S n = 180 ° ⋅ ( n − 2 )

где n – это количество углов в n -угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.

Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °

Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °

Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.

α n = 180 ° ⋅ ( n − 2 ) n

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с углами

🌟 Видео

Углы при параллельных и секущей #математика #огэматематика #огэ #данирСкачать

Углы при двух параллельных и секущей | Геометрия, 7 классСкачать

Углы при пересечении двух прямых третьейСкачать

Углы при пересечении двух прямых секущей (третьей прямой). Виды углов урок 5. Геометрия 7 класс.Скачать

Геометрия 7 класс | Вертикальные, смежные, накрест лежащие и другие углы (теория) | МАТЕМАТИКА 2021Скачать

Параллельные прямые (задачи).Скачать

29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

Это пора запомнить! Свойства углов при параллельных прямых и секущей. #геометрияСкачать

Параллельные прямые — Признак Параллельности Прямых и Свойства УгловСкачать