Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.
- Виды трапеции
- Свойства трапеции
- Свойства и признаки равнобедренной трапеции
- Формулы площади произвольной трапеции
- Формулы площади равнобедренной трапеции
- Формулы сторон произвольной трапеции
- Формулы сторон равнобедренной трапеции
- Формулы сторон прямоугольной трапеции
- Формулы диагоналей произвольной трапеции
- Формулы диагоналей равнобедренной трапеции
- Формулы диагоналей прямоугольной трапеции
- Формулы средней линии произвольной трапеции
- Формулы средней линии равнобедренной трапеции
- Формулы средней линии прямоугольной трапеции
- Формулы высоты произвольной трапеции
- Формулы высоты равнобедренной трапеции
- Формулы боковых сторон прямоугольной трапеции
- Трапеция. Формулы, признаки и свойства трапеции
- Основные свойства трапеции
- Сторона трапеции
- Формулы определения длин сторон трапеции:
- Средняя линия трапеции
- Формулы определения длины средней линии трапеции:
- Высота трапеции
- Формулы определения длины высоты трапеции:
- Диагонали трапеции
- Формулы определения длины диагоналей трапеции:
- Площадь трапеции
- Формулы определения площади трапеции:
- Периметр трапеции
- Формула определения периметра трапеции:
- Окружность описанная вокруг трапеции
- Формула определения радиуса описанной вокруг трапеции окружности:
- Окружность вписанная в трапецию
- Формула определения радиуса вписанной в трапецию окружности
- Другие отрезки разносторонней трапеции
- Формулы определения длин отрезков проходящих через трапецию:
- Трапеция. Свойства трапеции
- Свойства трапеции
- Свойства и признаки равнобедренной трапеции
- Вписанная окружность
- Площадь
- 🔍 Видео
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
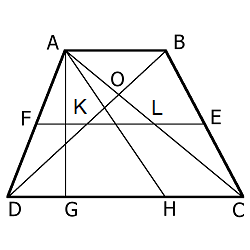
- Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме $$ FE = $$
- Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
- Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е. $$ KL = $$
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции
- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции
Площадь трапеции через основания и высоту
Площадь трапеции через среднюю линию и высоту
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через четыре стороны
Формулы площади равнобедренной трапеции

Площадь трапеции через стороны
Площадь трапеции через стороны и угол
$$ S = AD * sin(∠ADC) * (DC — AD * cos(∠ADC)) $$ $$ S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC)) $$
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$ S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB) $$
Площадь трапеции если в нее вписана окружность
Формулы сторон произвольной трапеции
Основание через другое основание и среднюю линию
$$ AB = 2 * FE — DC $$ $$ DC = 2 * FE — AB $$
Основание через другое основание, диагонали и угол между ними
$$ DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ AB = DC — AG * (ctg(∠ADC) + ctg(∠BCD)) $$ $$ DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD) $$ $$ AB = DC — AD * cos(∠ADC) — BC * cos(∠BCD) $$ $$ AD = $$ $$ BC = $$
Формулы сторон равнобедренной трапеции

$$ AD = $$ $$ AD = $$ $$ DC = AB + 2 * AG * ctg(∠ADC) $$ $$ AB = DC — 2 * AG * ctg(∠ADC) $$ $$ DC = AB + 2 * AB * cos(∠ADC) $$ $$ AB = DC — 2 * AB * cos(∠ADC) $$
Длина основания через диагональ, боковую сторону и другое основание
Длина боковой стороны через диагональ и основания
Длина основания через высоту, другое основание, диагонали и угол между ними
Длина основания через высоту, другое основание и площадь трапеции
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
Длина боковой стороны через площадь трапеции, основания и угол при основании
Формулы сторон прямоугольной трапеции
$$ DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD) $$ $$ AB = DC — BC * cos(∠BCD) = DC — AD * ctg(∠BCD) $$ $$ DC = AB + sqrt $$ $$ AB = DC — sqrt $$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG) $$ DC = — AB $$ $$ AB = — DC $$
Формулы диагоналей произвольной трапеции
Длина диагоналей через четыре стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту
Длина диагоналей через стороны и другую диагональ
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
Формулы диагоналей равнобедренной трапеции

Длина диагоналей через стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту основание и угол при основании
Длина диагоналей через сторону и высоту
Формулы диагоналей прямоугольной трапеции
Формулы средней линии произвольной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и высоту
Формулы средней линии равнобедренной трапеции

Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
$$ FE = DC — AG * ctg(∠ADC) = AB + AG * ctg(∠ADC) $$
Длина средней линии через основания, боковую сторону и высоту
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и боковую сторону
Формулы средней линии прямоугольной трапеции
Длина средней линии через основания, высоту и угол при нижнем основании
Длина средней линии через основания, боковую сторону и угол при нижнем основании
Длина средней линии через основания и боковые стороны
Длина средней линии через диагонали, высоту и угол между диагоналями
Формулы высоты произвольной трапеции
Длина высоты через четыре стороны
Длина высоты через боковую сторону и прилегающий угол к основанию
$$ AG = AD * sin(∠ADC) = BC * sin(∠BCD) $$
Длина высоты через диагонали и углы между ними
Длина высоты через среднюю линию, диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы высоты равнобедренной трапеции

Длина высоты через по сторонам
Длина высоты через боковую сторону и прилегающий угол к основанию
Длина высоты через основания и прилегающий угол к основанию
Длина высоты через диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы боковых сторон прямоугольной трапеции
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
Сторона BC через основания и угол ∠BCD
Сторона BC через Сторону AD
Сторона BC через площадь, среднюю линию и угол ∠BCD
Сторона BC через площадь, основания и угол ∠BCD
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Трапеция. Формулы, признаки и свойства трапеции
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
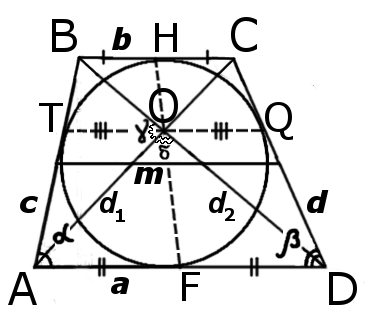 | 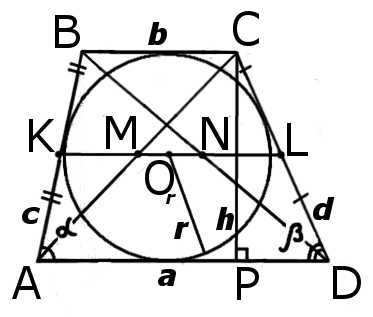 |
| Рис.1 | Рис.2 |
Видео:Радиус описанной окружности трапецииСкачать

Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Сторона трапеции
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a — h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a — c· cos α — d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Средняя линия трапеции
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Высота трапеции
Формулы определения длины высоты трапеции:
h = c· sin α = d· sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d 1 d 2 | = | sin δ · | d 1 d 2 |
| 2 m | 2 m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Диагонали трапеции
Формулы определения длины диагоналей трапеции:
d 1 = √ a 2 + d 2 — 2 ad· cos β
d 2 = √ a 2 + c 2 — 2 ac· cos β
2. Формулы диагоналей через четыре стороны:
| d 1 = | √ | d 2 + ab — | a ( d 2 — c 2 ) |
| a — b |
| d 2 = | √ | c 2 + ab — | a ( c 2 — d 2 ) | a — b |
d 1 = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2
d 2 = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2
d 1 = √ c 2 + d 2 + 2 ab — d 2 2
d 2 = √ c 2 + d 2 + 2 ab — d 1 2
Видео:КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
| S = | ( a + b ) | · h |
| 2 |
3. Формула площади через диагонали и угол между ними:
| S = | d 1 d 2 | · sin γ | = | d 1 d 2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c 2 — | ( | ( a — b ) 2 + c 2 — d 2 | ) | 2 |
| 2 | 2( a — b ) |
5. Формула Герона для трапеции
| S = | a + b | √ ( p — a )( p — b )( p — a — c )( p — a — d ) |
| | a — b | |
где
| p = | a + b + c + d | — полупериметр трапеции. |
| 2 |
Видео:Задача про трапецию, описанную около окружностиСкачать

Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
Видео:Окружность и трапеция | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис Трушин +Скачать

Окружность описанная вокруг трапеции
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d 1 |
| 4√ p ( p — a )( p — c )( p — d 1) |
где
| p = | a + c + d 1 |
| 2 |
a — большее основание
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Окружность вписанная в трапецию
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:Окружность, вписанная в трапециюСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Трапеция и вписанная окружностьСкачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
🔍 Видео
Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

8 класс, 6 урок, ТрапецияСкачать

Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать