Треугольник abc треугольнику a1b1c1

Видео:№548. Треугольники ABC и А1В1С1 подобны. Сходственные стороны ВС и В1С1 соответственно равныСкачать

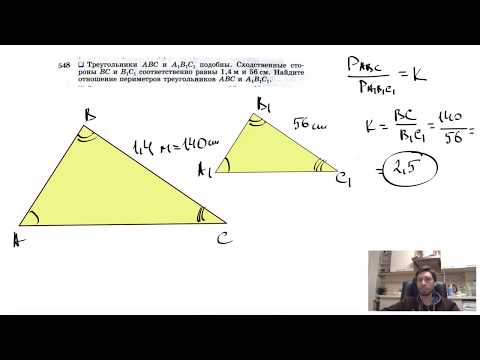
Ваш ответ

Видео:№560. Подобны ли треугольники ABC и A1B1C1, если: а) АВ = 3 см, ВС=5 см, СА=7 см, А1В1=4,5см,Скачать

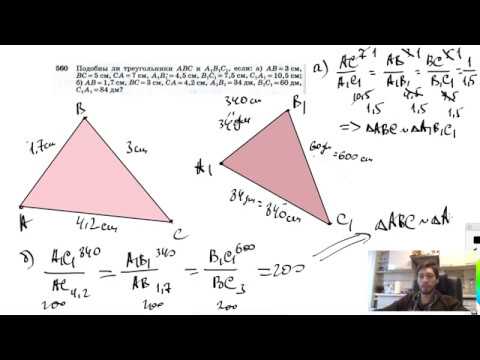
решение вопроса

Видео:Геометрия Дано: треугольник ABC подобен треугольнику A1B1C1, AB = 6 см, BC = 7 см, угол A равенСкачать

Похожие вопросы

• Все категории
• экономические 43,280
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,971
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№130. В треугольниках ABC и А1В1С1 отрезки СО и С1О1 — медианы, ВС=В1С1, ∠B = ∠B1 и ∠C=∠C1Скачать

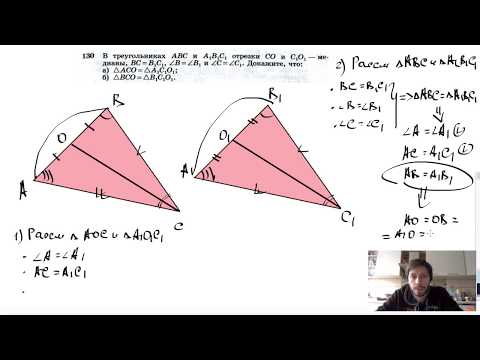
Треугольник abc треугольнику a1b1c1

§ 8. Первый и второй признаки равенства треугольников

Если для треугольников ABC и A 1 B 1 C 1 выполняются шесть условий: ∠ A = ∠ A 1 , ∠ B = ∠ B 1 , ∠ C = ∠ C 1 , AB = A 1 B 1 , BC = B 1 C 1 , CA = C 1 A 1 , то очевидно, что эти треугольники совпадут при наложении. Значит, они равны.

Попробуем уменьшить количество условий. Например, оставим лишь два равенства: AB = A 1 B 1 и BC = B 1 C 1 . В этом случае треугольники ABC и A 1 B 1 C 1 могут оказаться неравными (рис. 125).

Как же сократить список требований до минимума, но при этом сохранить равенство треугольников? На этот вопрос отвечают теоремы, которые называют признаками равенства треугольников .

(первый признак равенства треугольников: по двум сторонам и углу между ними)

Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых AB = A 1 B 1 , BC = B 1 C 1 , ∠ B = ∠ B 1 (рис. 126). Докажем, что ∆ ABC = ∆ A 1 B 1 C 1 .

Наложим ∆ ABC на ∆ A 1 B 1 C 1 так, чтобы луч BA совместился с лучом B 1 A 1 , а луч BC совместился с лучом B 1 C 1 . Это можно сделать, так как по условию ∠ B = ∠ B 1 . Поскольку по условию BA = B 1 A 1 и BC = B 1 C 1 , то при таком наложении сторона BA совместится со стороной B 1 A 1 , а сторона BC — со стороной B 1 C 1 . Следовательно, треугольники ABC и A 1 B 1 C 1 полностью совместятся, значит, они равны.

Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.

На рисунке 127 прямая a — серединный перпендикуляр отрезка AB , а точки A и B равноудалены от прямой a .

Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.

Пусть X — произвольная точка серединного перпендикуляра a отрезка AB , точка M — середина отрезка AB . Надо доказать, что XA = XB .

Если точка X совпадает с точкой M (а это возможно, так как X — произвольная точка прямой a ), то XA = XB .

Если точки X и M не совпадают, то рассмотрим треугольники AXM и BXM (рис. 128). В этих треугольниках AM = MB , так как точка M — середина отрезка AB , сторона XM — общая, ∠ AMX = ∠ BMX = 90°. Следовательно, треугольники AXM и BXM равны по первому признаку равенства треугольников. Значит, отрезки XA и XB равны как соответственные стороны равных треугольников.

(второй признак равенства треугольников: по стороне и двум прилежащим к ней углам)

Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Рассмотрим треугольники ABC и A 1 B 1 C 1 , у которых AC = A 1 C 1 , ∠ A = ∠ A 1 , ∠ C = ∠ C 1 (рис. 129). Докажем, что ∆ ABC = ∆ A 1 B 1 C 1 .

Наложим треугольник ABC на треугольник A 1 B 1 C 1 так, чтобы точка A совместилась с точкой A 1 , отрезок AC — с отрезком A 1 C 1 (это возможно, так как AC = A 1 C 1 ) и точки B и B 1 лежали в одной полуплоскости относительно прямой A 1 C 1 . Поскольку ∠ A = ∠ A 1 и ∠ C = ∠ C 1 , то луч AB совместится с лучом A 1 B 1 , а луч CB — с лучом C 1 B 1 . Тогда точка B — общая точка лучей AB и CB — совместится с точкой B 1 — общей точкой лучей A 1 B 1 и C 1 B 1 . Значит, треугольники ABC и A 1 B 1 C 1 полностью совместятся, следовательно, они равны.

Задача. На рисунке 130 точка O — середина отрезка BD , ∠ ABO = ∠ CDO . Докажите, что BC = AD .

Решение. Рассмотрим ∆ AOB и ∆ COD . Так как точка O — середина отрезка BD , то BO = OD . По условию ∠ ABO = ∠ CDO . Углы AOB и COD равны как вертикальные. Следовательно, ∆ AOB = ∆ COD по стороне и двум прилежащим углам.

Отсюда AB = CD , ∠ BAC = ∠ DCA . Заметим, что AC — общая сторона треугольников ABC и ADC . Следовательно, ∆ ABC = ∆ ACD по двум сторонам и углу между ними. Тогда BC = AD .

1. Сформулируйте первый признак равенства треугольников.
2. Какую прямую называют серединным перпендикуляром отрезка?
3. Каким свойством обладают точки серединного перпендикуляра?
4. Сформулируйте второй признак равенства треугольников.

154. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 и 6 см, а угол между ними — 40°.

155. С помощью линейки и транспортира постройте треугольник, две стороны которого равны 3 см и 4 см, а угол между ними — 90°. Укажите вид этого треугольника.

156. С помощью линейки и транспортира постройте треугольник, одна сторона которого равна 3 см, а углы, прилежащие к этой стороне, — 100° и 20°. Укажите вид этого треугольника.

157. С помощью линейки и транспортира постройте треугольник, одна сторона которого равна 6 см, а углы, прилежащие к этой стороне, — 90° и 45°.

158. Перерисуйте в тетрадь рисунок 131. С помощью угольника и линейки найдите на прямой l точку, равноудалённую от концов отрезка AB .

159. Перерисуйте в тетрадь рисунок 132. С помощью угольника и линейки найдите точку, равноудалённую от точек A и B , а также точек C и D .

160. На рисунке 133 AC = DC , BC = EC . Докажите, что ∆ ABC = ∆ DEC .

161. На рисунке 134 AB = AD , ∠ BAC = ∠ DAC . Докажите, что ∆ ABC = ∆ ADC .

162. На рисунке 135 AB = CD , ∠ 1 = ∠ 2, AD = 7 см, ∠ C = 34°. Найдите отрезок BC и угол A .

163. На рисунке 136 AO = OD , BO = OC . Найдите сторону CD и угол OCD треугольника OCD , если AB = 8 см, ∠ OBA = 43°.

164. Дано: OA = OC , OB = OD (рис. 137). Докажите, что ∠ OAD = ∠ OCB .

165. Дано: AD ⊥ BC , BD = CD (рис. 138). Докажите, что AB = AC .

166. Из точек A и B , лежащих в одной полуплоскости относительно прямой a и на одинаковом расстоянии от неё, опущены на эту прямую перпендикуляры AC и BD . Найдите угол ACB , если ∠ ADC = 25°.

167. Отрезки AD и BC пересекаются в точке O и делятся этой точкой пополам. Найдите угол ACD , если ∠ ABC = 64°, ∠ ACO = 56°.

168. На рисунке 139 AB ⊥ BD , CD ⊥ BD , точка O — середина отрезка BD . Докажите, что ∆ ABO = ∆ CDO .

169. На рисунке 140 ∠ 1 = ∠ 2, ∠ 3 = ∠ 4, AB = 8 см, BC = 6 см. Найдите стороны AD и CD треугольника ADC .

170. На рисунке 141 ∠ ABC = ∠ DEF , BO = OE . Докажите, что ∆ BCO = ∆ EFO .

171. На рисунке 142 ∠ BAO = ∠ DCO , ∠ BAC = ∠ DCA . Докажите, что ∆ ABC = ∆ ACD .

172. На сторонах угла с вершиной в точке B отмечены точки A и C , а на его биссектрисе — точка D так, что ∠ ADB = ∠ CDB . Докажите, что AB = BC .

173. Через точку M , принадлежащую биссектрисе угла с вершиной в точке O , провели прямую, перпендикулярную биссектрисе. Эта прямая пересекает стороны данного угла в точках A и B . Докажите, что AM = MB .

174. На рисунке 143 ∆ ABC = ∆ ADC . Докажите, что ∆ ABK = ∆ ADK .

175. На рисунке 144 ∆ ABC = ∆ A 1 B 1 C 1 , ∠ DBC = ∠ D 1 B 1 C 1 . Докажите, что ∆ DBC = ∆ D 1 B 1 C 1 .

176. На рисунке 145 ∆ MKO = ∆ MPO . Докажите, что ∆ KOE = ∆ POE .

177. На рисунке 146 BM ⊥ AD , CK ⊥ AD , BM = CK , AM = KD . Докажите, что ∆ ABD = ∆ ADC .

178. Докажите, что в равных треугольниках биссектрисы соответственных углов равны.

179. Докажите, что в равных треугольниках медианы, проведённые к соответственным сторонам, равны.

180. На продолжении медианы AM треугольника ABC за точку M отложен отрезок MK , равный AM . Найдите расстояние от точки K до вершины C , если AB = 6 см.

181. Отрезки AB и CD пересекаются в точке O и делятся точкой пересечения пополам. Докажите, что ∆ ABC = ∆ BAD .

182. На рисунке 147 прямые m и n — серединные перпендикуляры сторон AB и AC треугольника ABC . Докажите, что точка O равноудалена от всех вершин данного треугольника.

183. Для нахождения расстояния от точки B до колокольни A , расположенной на другом берегу реки (рис. 148), с помощью вешек, рулетки и астролябии отметили на местности точки C , D и E так, что B , C и D лежат на одной прямой, причём точка C является серединой отрезка BD , и наметили прямую AE , проходящую через точку C , причём ∠ ABC = ∠ CDE . Потом, измерив одну из сторон треугольника CDE , определили расстояние от B до A . Какую сторону измерили? Ответ обоснуйте.

184. Для определения ширины озера (рис. 149) на его берегу отметили точки A и B , а потом ещё точки C , D и O так, что точка O — общая середина отрезков AC и BD . Как можно определить ширину озера? Ответ обоснуйте.

185. Докажите равенство двух треугольников по стороне, медиане, проведённой к этой стороне, и углу между этой стороной и медианой.

186. Докажите равенство двух треугольников по стороне, прилежащему к ней углу и биссектрисе этого угла.

187. Докажите равенство двух треугольников по биссектрисе, углу, из вершины которого проведена эта биссектриса, и углу, образованному биссектрисой со стороной, к которой она проведена.

188. Серединный перпендикуляр стороны BC треугольника ABC пересекает его сторону AB в точке D . Найдите длину отрезка AD , если CD = 4 см, AB = 7 см.

189. Серединный перпендикуляр стороны AB треугольника ABC пересекает его сторону BC в точке M . Найдите длину стороны AC треугольника ABC , если BC = 16 см, а периметр треугольника AMC равен 26 см.

190. На рисунке 150 OA = OD . Добавьте ещё одно условие так, чтобы треугольники АОС и DOB оказались равными:

1) по первому признаку равенства треугольников;

2) по второму признаку равенства треугольников.

191. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. На отрезке AC отмечена точка M , а на отрезке BD — точка K так, что AM = BK . Докажите, что: 1) OM = OK ; 2) точки M , O и K лежат на одной прямой.

192. На одной стороне угла с вершиной в точке O (рис. 151) отмечены точки A и B , а на другой — точки C и D так, что OA = OC , AB = CD . Докажите, что луч OM является биссектрисой угла BOD , где M — точка пересечения отрезков AD и BC .

Упражнения для повторения

193. Истинно ли утверждение: если через каждые две из трёх данных точек провести прямую, то получим три прямые?

194. Лучи OD и OF — биссектрисы смежных углов AOB и BOC соответственно, ∠ AOD : ∠ FOC = 2 : 7. Найдите ∠ AOD и ∠ FOC .

Наблюдайте, рисуйте, конструируйте, фантазируйте

195. Разделите каждую из фигур, изображённых на рисунке 152, по линиям сетки на четыре равные части так, чтобы в каждой части был ровно один кружок.

📽️ Видео

№127. В треугольниках ABC и А1В1С1 АВ=А1В1, ВС=В1С1, ∠B =∠B1Скачать

№98. В треугольниках ABC и A1B1C1 AB = А1В1, АС = А1С1, ∠A=∠A1 На сторонах AB и A1B1 отмеченыСкачать

№545. Треугольники ABC и А1В1С1 подобны, и их сходственные стороны относятся как 6:5Скачать

№140. В треугольниках ABC и А1B1С1 медианы ВМ и B1М1 равны, АВ =А1B1, АС=А1С1. Докажите, что ΔABCСкачать

№141. В треугольниках ABC и А1В1С1 отрезки AD и A1D1 — биссектрисы, АВ=А1В1, BD = B1D1 и AD=A1D1.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№262 В треугольниках ABC и А1В1С1 углы А и А1 — прямые, BD и В1D1— биссектрисы. Докажите, чтоСкачать

№161. В треугольниках ABC и А1B1С1 медианы AM и А1М1 равны, BC=B1С1 и ∠AMB=∠A1M1B1. Докажите, чтоСкачать

Геометрия Подобны ли треугольники ABC и A1B1C1, если: 1) AB = 6 см, BC = 10 см, AC = 14 смСкачать

№177* Даны два треугольника: ABC и А1В1С1. Известно, что АВ=А1В1, АС=А1С1, ∠A=∠A1. На сторонах АССкачать

№170. Докажите, что треугольники ABC и А1B1С1 равны, если АВ =А1В1, ∠A=∠A1, AD =A1D1, где AD и A1D1Скачать

№269. Докажите, что ΔАВС=ΔА1B1С1, если ∠A=∠A1, ∠B=∠B1 и ВН=В1Н1, где ВН и В1Н1Скачать

Геометрия В треугольниках ABC и A1B1C1 известно, что угол A = углу A1, угол B = углу B1, AB = 6 смСкачать

№176* Докажите, что треугольники ABC и А1В1С1 равны, если АВ=А1В1, АС=А1С1, АМ=А1М1, где AM и А1М1Скачать

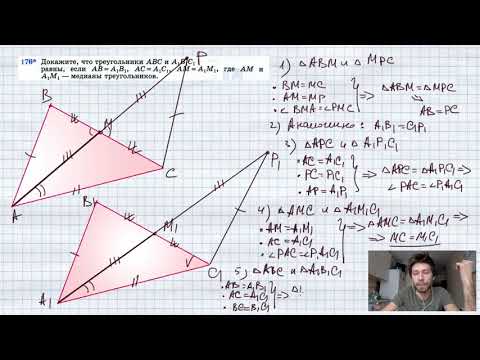
Геометрия В треугольниках ABC и A1B1C1 известно, что угол A = углу A1, каждая из сторон AB и ACСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать