- ЕГЭ формулы, шпаргалки — Элементарная геометрия. Окружность и круг.
- Площадь круга и его частей. Длина окружности и ее дуг
- Основные определения и свойства
- Формулы для площади круга и его частей
- Формулы для длины окружности и её дуг
- Площадь круга
- Длина окружности
- Длина дуги
- Площадь сектора
- Площадь сегмента
- Основные теоремы, связанные с окружностями
ЕГЭ формулы, шпаргалки — Элементарная геометрия. Окружность и круг.
.
,
где S — площадь круга,
R — радиус круга,
D — диаметр круга,
Полный список всех формул, шпаргалок для ЕГЭ по математике тут: ЕГЭ математика — формулы, шпаргалки.
Площадь круга и его частей. Длина окружности и ее дуг
 Основные определения и свойства. Число π |
| Формулы для площади круга и его частей |
| Формулы для длины окружности и ее дуг |
| Площадь круга |
| Длина окружности |
| Длина дуги |
| Площадь сектора |
| Площадь сегмента |
Основные определения и свойства
| Фигура | Рисунок | Определения и свойства | ||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||
| Дуга |  | |||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||
| Сектор |  | |||||||||||||||||||||||||
| Сегмент |  | |||||||||||||||||||||||||
| Правильный многоугольник |  | |||||||||||||||||||||||||
 |
| Окружность |
|
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула | |||||||||
| Площадь круга |  | ||||||||||
| Площадь сектора |  | ||||||||||
| Площадь сегмента |  |
| Площадь круга |
|
,
где R – радиус круга, D – диаметр круга
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула | |
| Длина окружности |  | ||
| Длина дуги |  |
| Длина окружности |
|
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Основные теоремы, связанные с окружностями
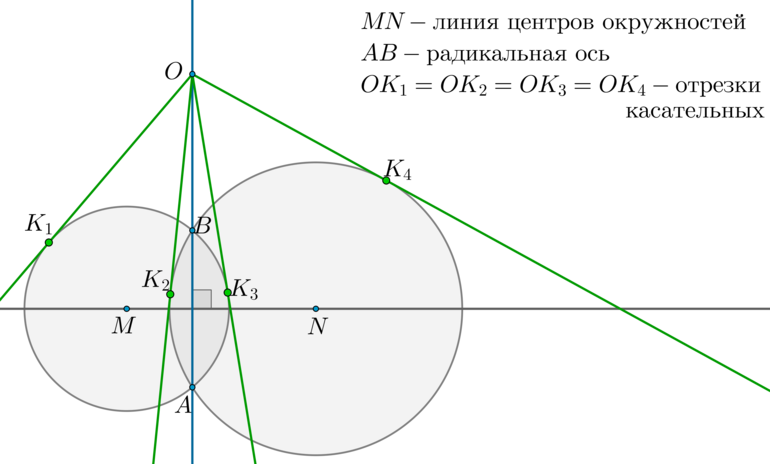
Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Теорема 1.
1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
Доказательство:
1) Рассмотрим (triangle BMN) и (triangle AMN) : они равны по трем сторонам ( (BM=AM=R_1, BN=AN=R_2) — радиусы первой и второй окружностей соответственно). Таким образом, (angle BNM=angle ANM) , следовательно, (MN) — биссектриса в равнобедренном (triangle ANB) , следовательно, (MNperp AB) .
2) Отметим произвольную точку (O) на радикальной оси и проведем касательные (OK_1, OK_3) к первой окружности и (OK_2, OK_4) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то (OK_1^2=OK_2^2=OK_3^2=OK_4^2=OBcdot OA) .
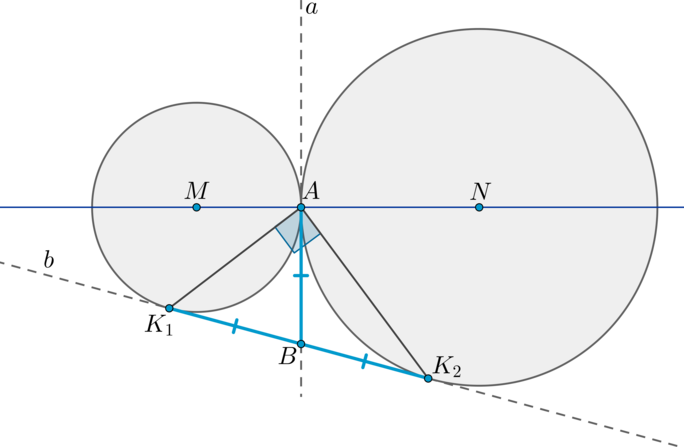
Теорема 2.
Пусть две окружности с центрами (M) и (N) касаются внешним образом в точке (A) . Две общие касательные (внутренняя и внешняя) (a) и (b) этих окружностей пересекаются в точке (B) . Точки касания — точки (A, K_1, K_2) (как показано на рисунке). Тогда [(1) <large>] [(2) <large>]
Доказательство:
1) Т.к. (BA) и (BK_1) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: (BA=BK_1) . Аналогично, (BA=BK_2) . Таким образом, (BA=BK_1=BK_2) .
2) Значит, (BA) — медиана в (triangle K_1AK_2) , равная половине стороны, к которой она проведена. Значит, (angle A=90^circ) .
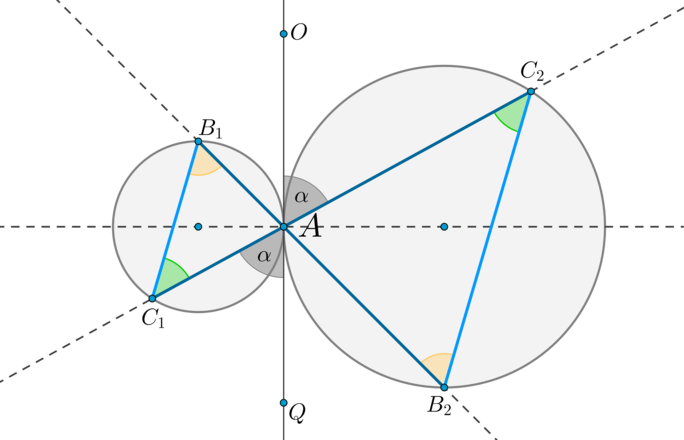
Теорема 3.
Пусть две окружности касаются внешним образом в точке (A) . Через точку (A) проведены две прямые (B_1B_2) и (C_1C_2) , пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: [(1) <large>] [(2) <large>]
Доказательство:
1) Проведем через точку (A) общую касательную этих окружностей (OQ) . (angle OAC_2=angle QAC_1=alpha) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то (angle OAC_2=frac12buildrelsmileover) , (angle QAC_1=frac12buildrelsmileover) . Следовательно, (buildrelsmileover=buildrelsmileover=2alpha) . Таким образом, (angle AB_1C_1=angle AB_2C_2=alpha) . Значит, по двум углам (triangle AB_1C_1sim triangle AB_2C_2) .
2) Т.к. (angle AB_1C_1=angle AB_2C_2) , то прямые (B_1C_1parallel B_2C_2) по накрест лежащим углам при секущей (B_1B_2) .
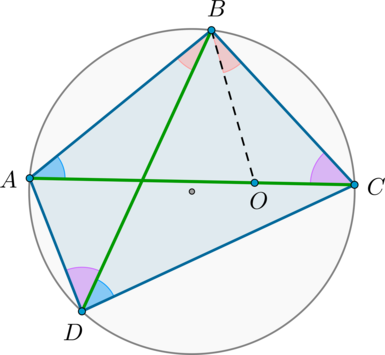
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: [ACcdot BD=ABcdot CD+BCcdot AD]
Доказательство
Пусть для определенности (angle ABD . Проведем отрезок (BO) так, чтобы (O) лежала на (AC) и (angle ABD=angle CBO) :
Т.к. (angle ACB=angle ADB) (опираются на одну и ту же дугу), то по двум углам (triangle OBCsim triangle ABD) . Значит: [dfrac=dfrac Rightarrow ADcdot BC=OCcdot BDphantom (1)]
Т.к. (angle BAC=angle BDC) (опираются на одну и ту же дугу), (angle ABO=angle CBD) (состоят из равных по построению (оранжевых) углов и общего угла (angle DBO) ), то по двум углам (triangle ABOsim triangle BDC) . Значит: [dfrac=dfrac Rightarrow ABcdot CD=AOcdot BD phantom (2)]
Сложим равенства ((1)) и ((2)) : (ADcdot BC+ABcdot CD=OCcdot BD+AOcdot BD=ACcdot BD) , чтд.
Формула Эйлера:
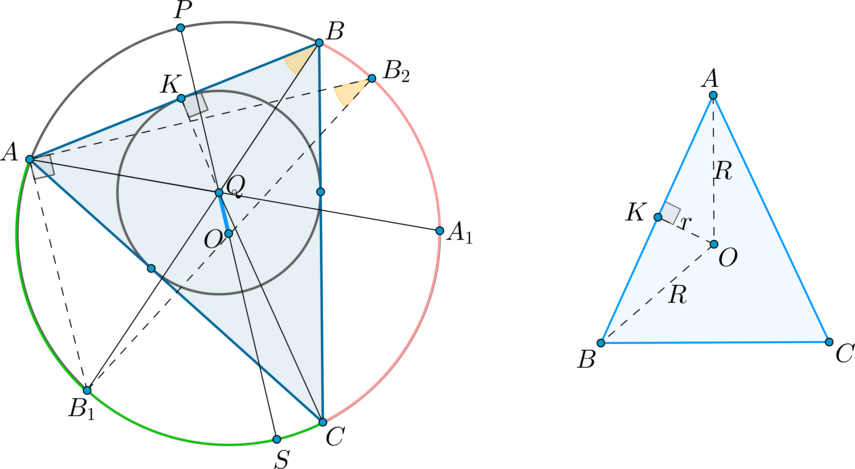
Пусть (R) — радиус описанной около треугольника (ABC) окружности, (r) — радиус вписанной окружности. Тогда расстояние (d) между центрами этих окружностей вычисляется по формуле: [<large>] 
Доказательство:
а) Предположим, что (dne 0) . Пусть (O, Q) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности (PS) через точку (Q) . Проведем также биссектрисы углов (angle A, angle B) — (AA_1, BB_1) соответственно (заметим, что они пересекутся в точке (Q) , т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды (PS) и (BB_1) пересекаются, следовательно, отрезки этих хорд равны: (PQcdot QS=BQcdot QB_1) .
Т.к. (OP=OS=R, OQ=d) , то последнее равенство можно переписать в виде ((R-d)(R+d)=BQcdot QB_1 (*)) .
Заметим, что т.к. (AA_1, BB_1) — биссектрисы, то (buildrelsmileover=buildrelsmileover=x, buildrelsmileover=buildrelsmileover=y) . Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
(angle AQB_1=frac12(x+y)) .
С другой стороны, (angle B_1AA_1=frac12big(buildrelsmileover+buildrelsmileoverbig)=frac12(x+y))
Таким образом, (angle AQB_1=angle B_1AA_1) . Следовательно, (triangle QB_1A) — равнобедренный и (B_1Q=B_1A) . Значит, равенство ((*)) можно переписать как:
(R^2-d^2=BQcdot AB_1 (**)) .
Проведем еще один диаметр описанной окружности (B_1B_2) . Тогда (triangle B_1AB_2) — прямоугольный ( (angle A) опирается на диаметр). Пусть также вписанная окружность касается стороны (AB) в точке (K) . Тогда (triangle BKQ) — прямоугольный.
Заметим также, что (angle KBQ=angle AB_2B_1) (т.к. они опираются на одну и ту же дугу).
Значит, (triangle B_1AB_2sim triangle BKQ) по двум углам, следовательно:
(dfrac=dfrac Rightarrow dfrac=dfrac Rightarrow BQcdot AB_1=2Rr) .
Подставим это в ((**)) и получим:
(R^2-d^2=2Rr Rightarrow d^2=R^2-2Rr) .
б) Если (d=0) , т.е. центры вписанной и описанной окружностей совпадают, то (AK=BK=sqrt Rightarrow AB=2sqrt) . Аналогично (AC=BC=AB=sqrt) , т.е. треугольник равносторонний. Следовательно, (angle A=60^circ Rightarrow angle KAO=30^circ Rightarrow r=frac12R Rightarrow R=2r) или (0=R^2-2Rr) (т.е. в этом случае формула также верна).
Теорема о бабочке:
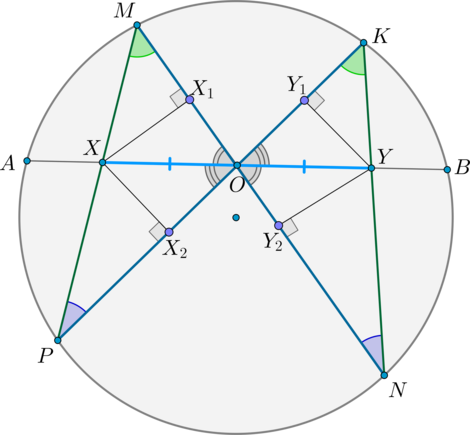
Пусть через середину хорды (AB) — точку (O) , проведены две хорды (MN) и (KP) . Пусть (MPcap AB=X, KNcap AB=Y) . Тогда [<large>]
Доказательство:
Проведем перпендикуляры (XX_1, YY_2perp MN, XX_2, YY_1perp KP) .
Следующие углы равны, т.к. опираются на одну и ту же дугу: (angle PMO=angle NKO, angle MPO=angle KNO) .
Следующие углы равны, т.к. вертикальные: (angle XOX_1=angle YOY_2, angle XOX_2=angle YOY_1) .
Следующие прямоугольные треугольники подобны:
1) (triangle XX_1Osim triangle YY_2O Rightarrow dfrac=dfrac)
2) (triangle XX_2Osim triangle YY_1O Rightarrow dfrac=dfrac)
3) (triangle MXX_1sim triangle KYY_1 Rightarrow dfrac=dfrac)
4) (triangle PXX_2sim triangle NYY_2 Rightarrow dfrac=dfrac)
Из 1) и 2) следует, что
Из 3) и 4) следует, что
Совместив последние два равенства, получим:
Заметим, что для пересекающихся хорд (AB) и (MP) : (AXcdot XB=MXcdot PX) . Аналогично (AYcdot YB=KYcdot NY) . Значит:
Обозначим (OX=x, OY=y, OA=OB=t Rightarrow)