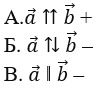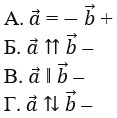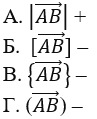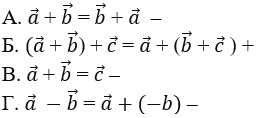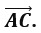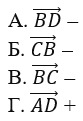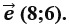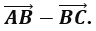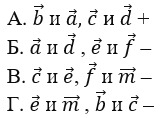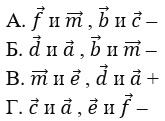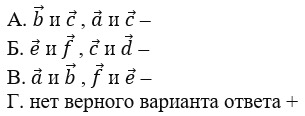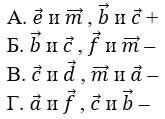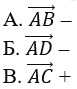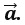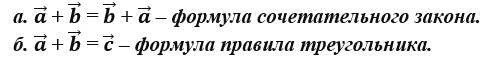Верны ли следующие суждения а векторы называются равными если они коллинеарные и их длины равны (5 видео)

Верны ли следующие суждения а векторы называются равными если они коллинеарные и их длины равны

Тесты по геометрии 9 класс. Тема: «Векторы»

Правильный вариант ответа отмечен знаком +

1. Отрезок, для которого указано, какой из его концов является началом, а какой – концом, называется:

Г. нет верного варианта ответа –

2. Любая точка пространства может рассматриваться как вектор. Такой вектор называется:

3. Два ненулевых вектора, лежащие на одной прямой или на параллельных прямых, называются:

В. противоположно направленными –

4. Какие слова пропущены в предложении?

Если два ненулевых вектора коллинеарны, то они могут быть направлены либо одинаково (тогда их называют …), либо противоположно (тогда их называют …).

А. сонаправленные; разнонаправленные –

Б. противоположно направленные: сонаправленные –

В. сонаправленные: противоположно направленные +

Г. нет верного варианта ответа –

5. Длиной ненулевого вектора 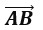называется:

Б. длина отрезка AB +

Г. нет верного варианта ответа –

6. Выберите верное обозначение сонаправленных векторов.

Г. нет верного варианта ответа –

7. Векторы называются равными, если:

А. они коллинеарны –

Б. их длины равны –

В. они сонаправлены –

Г. они сонаправлены и их длины равны +

8. Выберите верное обозначение противоположных векторов.

9. Выберите верное обозначение длины вектора

тест 10.

11. – это формула:

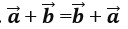
А. разности вектора –

Б. сочетательного закона –

В. нет верного варианта ответа –

Г. переместительного закона +

12. Выберите верную формулу сочетательного закона.

13. Вектор отложен от точки M. Точка M является:

А. концом вектора –

Б. началом вектора +

В. серединой вектора –

Г. нет верного варианта ответа –

14. Если длины двух ненулевых векторов равны, и они противоположно направлены, то они называются:

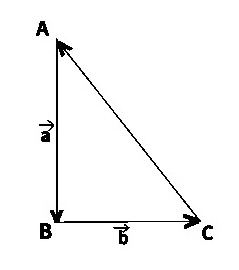
15. ABC – прямоугольный треугольник, 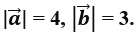Найдите длину вектора

16.

17. Найдите длину вектора

18. Дан правильный треугольник ABC со стороной 2. Найдите длину вектора

Г. недостаточно данных –

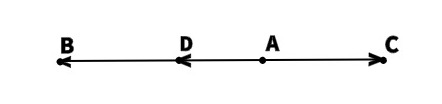
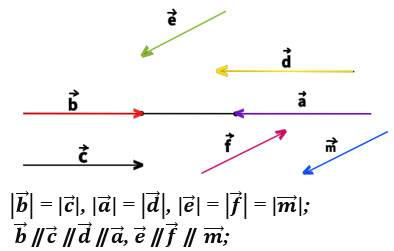
19. Выберите пары противоположно направленных векторов.

тест-20. Выберите пары сонаправленных векторов.

21. Выберите пары противоположных векторов.

22. Выберите пары равных векторов.

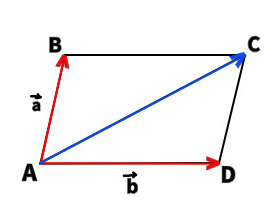
23. Дан параллелограмм ABCD, AC – диагональ Найдите сумму векторов

Г. нет верного варианта ответа –

24. Выберите верную формулировку правила многоугольника.

А. Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов. +

Б. От любой точки можно отложить вектор, равный данному, и притом только один. –

В. Чтоб сложить два вектора, нужно из произвольной точки отложить один вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало одного с концом второго. –

Г. Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов. –

25. Верны ли следующие суждения?

а. Векторы называются равными, если они коллинеарные и их длины равны.

б. Длиной нулевого вектора 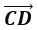является длина отрезка CD.

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

26. Верны ли следующие суждения?

а. Направленный отрезок (вектор), длина которого равна нулю, – это нулевой вектор.

б. От любой точки можно отложить вектор, равным данному, и притом только один.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

27. Верны ли следующие суждения?

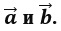
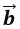
а. Разностью векторов называется такой вектор, сумма которого с вектором равна вектору

б. Два ненулевых вектора называются коллинеарными, если их длины равны и они противоположно направлены.

А. верно только а +

Б. верно только б –

В. оба суждения верны –

Г. оба суждения неверны –

28. Верны ли следующие суждения?

А. верно только а –

Б. верно только б +

В. оба суждения верны –

Г. оба суждения неверны –

29. Верны ли следующие суждения?

а. Вектор называется нулевым, если его начальная и конечная точка совпадает.

б. Модулем вектора называется длина вектора, выраженная числовым выражением.

А. верно только а –

Б. верно только б –

В. оба суждения верны +

Г. оба суждения неверны –

тест_30. Верны ли следующие суждения?

а. Скалярные величины характеризуются числом и направлением, а векторные только числом.

б. К векторным величинам относятся скорость, ускорение, перемещение.

Содержание

ПОМОГИТЕ РЕШИТЬ К.Р. 1. Какое из следующих утверждений неверно? а) длиной ненулевого вектора АВ называется длина отрезка АВ; б) нулевой вектор считается сонаправленным любому вектору; в) разностью векторов а и b называется такой вектор. сумма которого с вектором b равна вектору а; г) векторы называются равными, если равны их длины.
Понятие вектора. Коллинеарные и равные векторы.
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
📽️ Видео

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

ПОМОГИТЕ РЕШИТЬ К.Р.
1. Какое из следующих утверждений неверно?
а) длиной ненулевого вектора АВ называется длина отрезка АВ;
б) нулевой вектор считается сонаправленным любому вектору;
в) разностью векторов а и b называется такой вектор. сумма которого с вектором b равна вектору а;
г) векторы называются равными, если равны их длины.

2. Упростите выражение:СС1+СВ+СД+А1В1, если ABCDA₁B₁C₁D₁ — параллелепипед.
а) AC ; б) 0 ; в) СВ1; г) DC ; д) BA .

3. Какие из следующих утверждений верны?
а) противоположные векторы равны;
б) Векторы, лежащие на двух прямых, перпендикулярных к одной плоскости, коллинеарны
в) произведение вектора на число является число;
г) Для сложения двух векторов на плоскости используют правило параллелограмма.

4. Дан куб ABCDA₁B₁C₁D₁ . Найдите угол между DC1 и СВ.

а) 45о; б) 30о; в) 135о ; г) 90о ; д) 60о .

5. Какие из следующих утверждений неверны?

а) векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости;
б) если вектор с можно разложить по векторам а и b, т.е. представить в виде с=ха+yb,
где х, y- некоторые числа, то векторы а, b, c компланарны;

в) для сложения трёх некомпланарных векторов используют правило параллелепипеда;
г) любые два вектора компланарны;

6.Известно, что 2 AC = AB + AD , тогда векторы AB, AD являются:

а) некомпланарными; б) сонаправленными; в) коллинеарными;

г) нулевыми; д) компланарными.

7. Даны параллелограммы ABCD и AB₁C₁D₁. Тогда векторы BB1, CC1, DD1:

а) нулевые; б) равные; в) противоположные; г) компланарные; д) некомпланарные.

8) Составить уравнение плоскости, проходящей через точку А и перпендикулярной прямой АВ, если А(-1,2,1), В(-3,1,-2).

10. Площадь треугольника равна 8. Угол между плоскостью треугольника и его ортогональной проекцией равен 45о. Найдите площадь ортогональной проекции треугольника.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Понятие вектора. Коллинеарные и равные векторы.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

При первом знакомстве с геометрией мы выясняли, какие геометрические фигуры являются простейшими. К ним относились: точка, прямая и отрезок. Отрезок, как нам уже известно, это часть прямой, ограниченная двумя точками. Эти точки мы называли концами отрезка. Отрезки обозначаются двумя заглавными латинскими буквами, причём не важно, какой из двух концов мы называем первым.

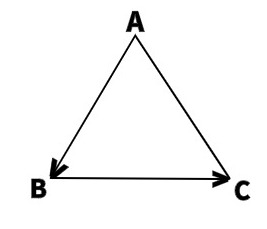
Рассмотрим такую ситуацию. Я купила в магазине муку и, поместив её в пакет, отправилась по прямой к остановке автобуса. По случайному стечению обстоятельств упаковка с мукой оказалась надорвана и пакет имел дырку. В результате весь мой путь от магазина до остановки был прочерчен просыпавшейся мукой. Получился такой белый отрезок. Но это ведь не простой отрезок, поскольку я шла только в одну сторону! Этот отрезок имел направление: от магазина до остановки. Вот такие направленные отрезки и называются векторами.

Определение. Вектором называется направленный отрезок, построенный по двум точкам, одна из которых считается началом, а другая – концом.

На рисунке представлен вектор с началом в точке и концом в точке . Обозначается он так: . Его уже нельзя обозначить , поскольку точка перемещается в точку , а не наоборот. Также, вектор можно обозначать одной маленькой буквой со стрелкой над ней , тогда на рисунке она располагается между началом и концом вектора.

Вектор, также как и отрезок, имеет длину.

Определение. Длиной вектора называется расстояние между его началом и концом. Другими словами, это длина отрезка, составляющего данный вектор.

Обозначается длина вектора так: или . О нахождении длины вектора поговорим позже.

Если конец вектора совпадает с его началом, то вектор называется нулевым, т.е. его длина равна нулю. Обозначается нулевой вектор так: или .

Отметьте три точки . Сколько векторов с началом и концом в этих точках можно провести? Проиллюстрируйте свой ответ.

Проведите векторы . Какая геометрическая фигура у вас получилась?

Проведите вектор . Что вы можете сказать о длине этого вектора?

На прямой отметьте два вектора с длинами 3 см и 1 см. Какие возможны варианты их расположения?

Начертите прямоугольник, проведите его диагонали. Отметьте все возможные векторы с началом и концом в видимых точках прямоугольника. Запишите их.

Начертите две параллельные прямые и . На прямой отложите вектор , а на прямой – вектор . Какие возможны варианты? Что вы можете сказать об этих векторах?

Рассмотрим теперь задание 6 из предыдущей темы. На двух параллельных прямых должны быть расположены два вектора. Рассмотрим варианты.

. Мы расположили эти векторы так, что они направлены в одну сторону. Такие векторы называются сонаправленными.

. Эти векторы мы расположили так, что они направлены в разные стороны. Такие векторы называются противоположно направленными.

Сонаправленные и противоположно направленные векторы составляют множество векторов, которое называется коллинеарными векторами.

Определение. Коллинеарными называются ненулевые векторы, лежащие на одной прямой или на параллельных прямых.

Определение. Сонаправленными называются коллинеарные векторы, если их концы лежат по одну сторону от прямой, проходящей через их начала (направленные в одну сторону). Обозначаются так: или .

Определение. Противоположно направленными называются коллинеарные векторы, если их концы находятся по разные стороны от прямой, проходящей через их начала (направленные в разные стороны). Обозначаются так: или .

В рассмотренных случаях мы заметили, что коллинеарные векторы имели разные длины. Однако, они могут иметь и одинаковую длину. От этого условие коллинеарности не нарушается. Но появляется новая группа векторов.

Определение. Равными называются сонаправленные векторы, имеющие равные длины. Обозначаются так: .

Значит, для того, чтобы векторы были равны, нужно, чтобы они лежали на параллельных прямых (или на одной прямой); были направлены в одну сторону и их длины должны быть равны.

Откладывание вектора от данной точки.

Утверждение. От любой точки плоскости можно отложить вектор, равный данному и, притом, только один.

Через точку проведём прямую , параллельную вектору . В соответствии с аксиомой IX планиметрии, такая прямая единственная.

На прямой от точки можно отложить два отрезка и одинаковой длины, равной длине вектора . Так как они отложены в разные стороны от точки , то векторы и противоположно направленные.

По определению равных векторов .

Для доказательства единственности такого вектора, предположим, что существует ещё один вектор с началом в точке , равный вектору . Пусть это будет вектор

Так как , то по определению равных векторов, они лежат на параллельных прямых. Значит, через точку проходят две прямые и , параллельные вектору . А это противоречит аксиоме IX .

Мы пришли к противоречию потому, что сделали неправильное предположение. Значит, вектор единственный, ч.т.д.