Верно ли утверждение что если прямая параллельна плоскости то она параллельна любой прямой лежащей

Прямая и плоскость могут пересекаться или быть параллельными друг другу. Еще один случай — прямая лежит в плоскости.

Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.

Это определение. Сложность только в одном — как на практике проверить, что бесконечная прямая нигде не пересечет бесконечную плоскость? Для практического применения используется признак параллельности прямой и плоскости:

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

Этот признак часто используется в решении задач по стереометрии. Например, в правильной четырехугольной пирамиде SABCD прямая АВ параллельна прямой СD — значит, АВ параллельна всей плоскости SCD.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Параллельность прямой и плоскости

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящен теме «Параллельность прямой и плоскости». На этом уроке мы обсудим параллельность прямой и плоскости как один из трех возможных вариантов их взаимного расположения в пространстве, рассмотрим ситуацию плоскость параллельная прямой. Сформулируем теорему и докажем ее и два утверждения, которые часто используются при решении задач на эту тему.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

10 класс. Геометрия. Параллельные прямые в пространстве.

10 класс. Геометрия. Параллельные прямые в пространстве.

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

1. Тема урока

Решение простейших задач на параллельность прямой и плоскости.

Видео:Ответы на вопросы к главе 1 - Геометрия 10-11 класс АтанасянСкачать

2. Определение параллельных прямых

Определение: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (Рис. 1.).

Видео:6. Параллельность прямой и плоскостиСкачать

3. Теорема о параллельных прямых

Теорема о параллельных прямых.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Пояснение к теореме

Дана прямая а, и точка М, не лежащая на ней: (Рис. 2.). Тогда через точку М проходит только одна прямая b, которая параллельная прямой а.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

4. Лемма

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Пояснение к лемме

Даны две параллельные прямые а и b. Прямая а пересекает плоскость в точке М. Лемма утверждает, что прямая b тоже пересекает плоскость в некоторой точке, назовем ее N (Рис. 3.).

Видео:Параллельность прямой к плоскостиСкачать

5. Теорема о трех параллельных прямых

Теорема о параллельности трех прямых.

Если две прямые параллельны третьей, то они параллельны.

Пояснение к теореме.

Даны три прямые а, b, с, такие, что а параллельна с и b параллельна с (Рис. 4.). Теорема утверждает, что прямая а параллельна прямой b.

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

6. Случаи взаимного расположения прямой и плоскости

Аксиома А2: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости

Из аксиомы А2 вытекают три случая взаимного расположения прямой и плоскости.

1) Прямая а целиком лежит в плоскости α: (Рис. 5.).

2) Прямая а имеет одну общую точку с плоскостью α:. Другими словами, прямая а и плоскость α пересекаются (Рис. 6.).

3) Прямая a не имеет общих точек с плоскостью α: (Рис. 7.).

Видео:№92. Плоскость α и прямая a параллельны прямой b. Докажите, что прямая a либо параллельна плоскостиСкачать

7. Определение параллельности прямой и плоскости

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

8. Признак параллельности прямой и плоскости

Теорема (признак параллельности прямой и плоскости)

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Пояснение к признаку.

Дана плоскость , прямая а, которая параллельна прямой b, лежащей в плоскости (Рис. 8.). Согласно признаку параллельности прямой и плоскости, этого достаточно, чтобы прямая а была параллельна всей плоскости.

Видео:№25. Докажите, что если данная прямая параллельна прямой, по которой пересекаютсяСкачать

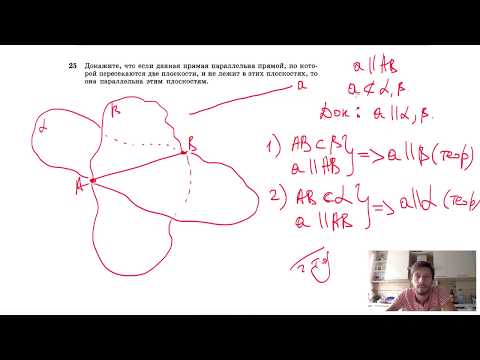
9. Утверждение 1

Из данного признака вытекает два утверждения, полезных для решения задач.

Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Дана плоскость и прямая а, которая параллельна плоскости (Рис. 9.). Через прямую а можно провести много плоскостей, которые пересекают плоскость . Проведем через прямую а плоскость . Согласно утверждению, линия пересечения плоскостей и – прямая b будет параллельна прямой а.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

10. Утверждение 2

Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Есть две параллельные прямые а и b и плоскость . Одна из параллельных прямых, например, прямая а, параллельна плоскости . Отсюда следует, согласно утверждению, что прямая b либо параллельна плоскости (Рис. 10.), либо лежит в плоскости (Рис. 11.).

Видео:№57. Прямая а параллельна одной из двух параллельных плоскостей. Докажите, что прямаяСкачать

11. Задача 1

Задача 1.

Параллельные прямые а и b лежат в плоскости . Докажите, что прямая с, пересекающая прямые а и b, также лежит в плоскости .

Дано: а || b,

Доказать:

Доказательство: (Рис. 12.)

Точка А прямой с, принадлежит и прямой а, а значит, и плоскости . Точка В прямой с принадлежит прямой b, а значит, и плоскости . Так как две точки прямой с принадлежат плоскости , то и вся прямая лежит в плоскости , в силу аксиомы А2.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

12. Задача 2

Задача 2.

Стороны AB и BC параллелограмма ABCD пересекают плоскость . Докажите, что прямые AD и DC также пересекают плоскость .

Дано: ABCD – параллелограмм,

Доказать: прямые AD и DC пересекают плоскость .

Доказательство: (Рис. 13.)

Обозначим плоскость АВС как . Тогда плоскости и пересекаются по прямой MN. Прямая АВ пересекается с плоскостью , и прямые АВ и CD параллельны (как стороны параллелограмма). Тогда, согласно лемме, прямая CD также пересекается с плоскостью . Аналогично, прямая ВCпересекается с плоскостью , и прямые ВС и АD параллельны (как стороны параллелограмма). Тогда, согласно лемме, прямая АD также пересекается с плоскостью , что и требовалось доказать.

Давайте найдем эти точки пересечения. Пусть прямая CD пересекается с плоскостью в точке Q, а прямая АD пересекается с плоскостью в точке F.

Плоскости и пересекаются по прямой MN, значит все их общие точки лежат на этой прямой. Продолжим прямые CD и АD до их пересечения с прямой MNи получим соответственно точки Q и F (Рис. 14.).

Видео:Параллельные плоскости и признак параллельности плоскостейСкачать

13. Задача 3

Задача 3.

Средняя линия трапеции лежит в плоскости , не совпадающей с плоскостью . Пересекаются ли прямые, содержащие основания трапеции, с плоскостью ?

Дано: ABCD – трапеция, MN – средняя линия.

Найти: пересекаются ли прямые AD и ВC плоскость .

Вспомним, что средняя линия трапеции параллельна ее основанием. Значит, прямые AD и MN параллельны, а прямая MN принадлежит плоскости . Значит, по признаку параллельности прямой и плоскости, AD параллельна плоскости .

Аналогично, прямые ВC и MN параллельны, а прямая MN принадлежит плоскости . Значит, по признаку параллельности прямой и плоскости, ВC параллельна плоскости .

Ответ задачи: нет, не пересекаются.

Видео:10 класс, 17 урок, Признак перпендикулярности прямой и плоскостиСкачать

14. Задача 4

Задача 4.

Точка D не лежит плоскости прямоугольника KLMN. Доказать, что MN || DKL.

Дано: KLMN – прямоугольник,

Доказать: MN || DKL

Доказательство: (Рис. 16.)

Прямые KL и MN параллельны, а прямая KL принадлежит плоскости DKL. Следовательно, по признаку параллельности прямой и плоскости, MN параллельна плоскости DKL, что и требовалось доказать.

Видео:№51. Докажите, что плоскости α и β параллельны, если две пересекающиеся прямые mСкачать

15. Итоги урока

Итак, мы рассмотрели теорию о параллельности прямой и плоскости, применили эту теорию к решению задач. Далее эта теория будет использована при рассмотрении вопроса о параллельности плоскостей.

📹 Видео

Параллельность прямой и плоскости. Решение задач по теме Параллельность прямых, прямой и плоскости.Скачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

№124. Прямая PQ параллельна плоскости α. Через точки Р и Q проведены прямые, перпендикулярныеСкачать