Метод наложения для треугольника (3 видео)

Урок геометрии в 7-м классе по теме «Признак равенства треугольников по двум сторонам и углу между ними»

Разделы: Математика

Цели:

Обучающая: учащиеся формулируют и доказывают первый признак равенства треугольников;
Развивающая: учащиеся учатся применять признак при решении задач;
Воспитательная: учащиеся осознают важность открытого признака.

Структура урока:

Мотивационно – ориентировочный этап.
1. Приветствие.
2. Контроль настроения.
3. Актуализация знаний (Фронтальный опрос).
4. Постановка учебной задачи.
Исполнительский этап.
1. Нахождение способа доказательства теоремы.
2. Проведение доказательства теоремы.
Рефлексивно – оценочный этап.
1. Решение задач.
2. Взаимооценка.
3. Домашнее задание.
4. Контроль настроения.

Оборудование: два треугольника из бумаги, линейка, проектор, компьютер с программой Microsoft Office Power Point, презентация.

Ход урока

І. Мотивационно-ориентировочный этап.

Приветствие.
Контроль настроения. (С помощью сигнальных карточек)
Актуализация знаний.

ІІІ Рефлексивно – оценочный этап.

Содержание

Признаки равенства треугольников
Первый признак равенства треугольников
Второй признак равенства треугольников
Третий признак равенства треугольников
Треугольники. Признаки равенства треугольников
Первый признак равенства треугольников
Второй признак равенства треугольников
Третий признак равенства треугольников
Задачи и решения
📽️ Видео

Видео:Метод наложения. Найти токи в цепи. #2Скачать

Признаки равенства треугольников

О чем эта статья:

Видео:Электротехника (ТОЭ). Лекция 8. Метод наложения токов | Решение задачСкачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Метод наложенияСкачать

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:Преобразование звезды сопротивлений в эквивалентный треугольник. Преобразование мостовой схемыСкачать

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Олимпиадная задача по ТОЭ #2. МЕТОД НАЛОЖЕНИЯ│Постоянный токСкачать

Треугольники. Признаки равенства треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

Действия учителя	Действия учащихся
— Какая фигура называется треугольником?	— Геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, соединенных отрезками, называется треугольником.
— Какие треугольники называются равными?	— Два треугольника называются равными, если их можно совместить наложением.
— Как установить равенство двух треугольников?	— Наложить один треугольник на другой, если они совместятся, то треугольники равны. Можно сравнить все стороны и углы одного треугольника со сторонами и углами другого.
— Все эти способы возможны, но они не всегда удобны, громоздки. А нет ли другого способа доказательства равенства двух треугольников?	— .
— Оказывается, равенство двух треугольников можно установить, не накладывая один треугольник на другой, а лишь сравнивая некоторые элементы этих фигур.	— .
Постановка учебной задачи.
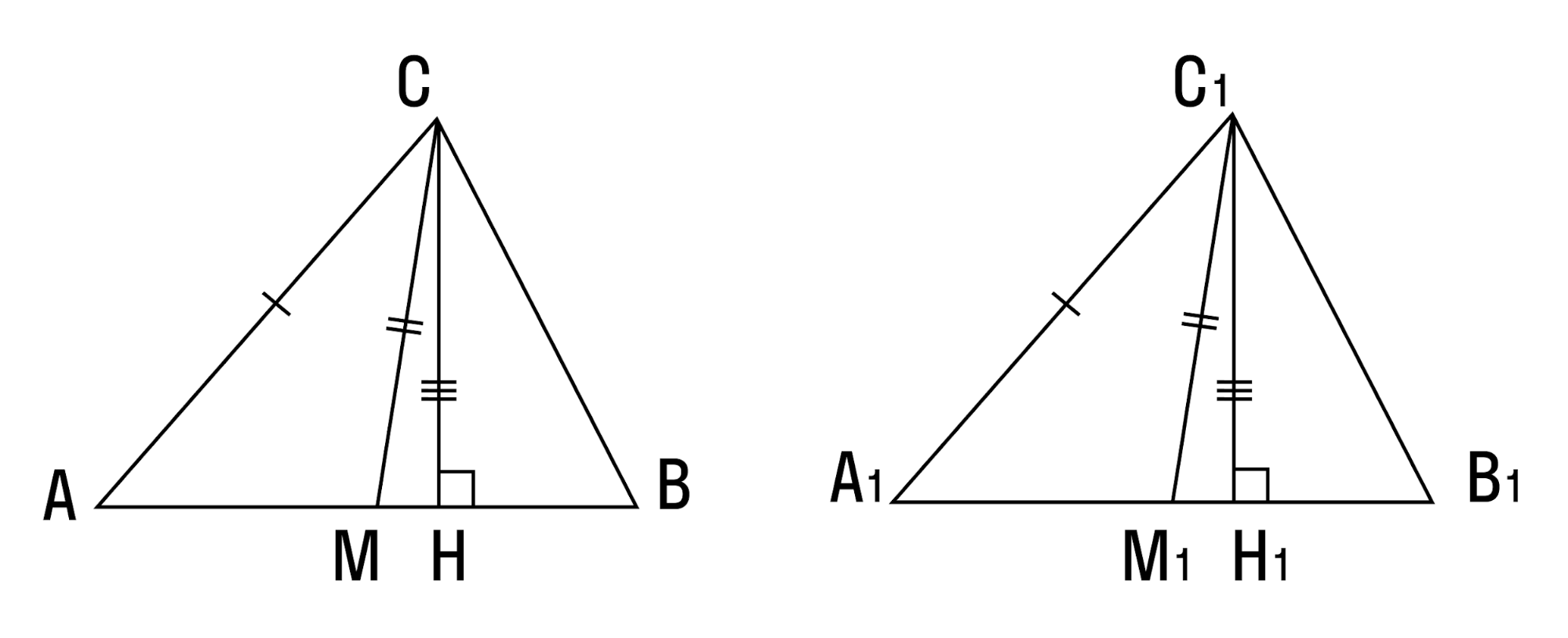
— Попробуем решить практическую задачу. Пусть надо измерить расстояние на местности от пункта А до пункта В, между которыми расположено озеро, поэтому с мерной лентой по прямой пройти нельзя. — На практике, для решения этой задачи поступают так: Выбирают некоторую точку С так, чтобы расстояние от точки С до точек А и В можно было измерить мерной лентой. Затем, на прямой АС отмечают точку К так, чтобы отрезок АС = СК, а на прямой ВС отмечают точку М так, чтобы отрезок ВС = СМ. Тогда на местности можно измерить расстояние МК, при этом утверждают, что оно равно искомому расстоянию между пунктами А и В.
— Почему можно утверждать, что МК = АВ? Когда можно найти другие равные элементы в треугольниках?	— Когда треугольники равны.
— Вероятно, ∆ АВС = ∆ МКС?
— А каким свойством обладают равные треугольники?	— В равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот, против равных углов, лежат равные стороны.
— Мы пока не знаем, равны наши треугольники или нет, ∆ АВС = ∆ МКС? Перечислите все равные элементы в этих треугольниках.	— АС = СК, ВС = СМ – по построению, ∠ АСВ = ∠ МСК как вертикальные.
— Итак, нам нужно установить равенство сторон АВ и МК, а равенство сторон следует из равенства треугольников. То есть, если мы докажем равенство треугольников, то равенство сторон будет доказано. Какова же цель урока?	— Доказать равенство треугольников.
— Используя равенства каких элементов?	— Двух сторон и угла между ними.
— Сформулируйте цель урока.
— Попробуем сформулировать утверждение, почему треугольники равны, по каким элементам?	— Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
— Данное утверждение называется теоремой. Теорема – утверждение, которое необходимо доказать, а сами рассуждения называют доказательством. Сформулированную теорему называют первым признаком равенства треугольников или признаком равенства треугольников по двум сторонам и углу между ними. (С этого этапа каждое обоснование сопровождается слайдом с презентации (приложение 1)) — Запишем в тетрадях тему. Признак равенства треугольников по двум сторонам и углу между ними. — Запишем формулировку теоремы. Теорема: Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. — Теорему можно назвать задачей, в которой есть условие, (то, что дано) и заключение, то, что необходимо доказать.
— В теореме, начиная со слова если до слова то является условием теоремы. Прочитайте условие теоремы.	— Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника.
— Все, что записано после слова то, называют заключением. Прочитайте заключение.	— Такие треугольники равны.
— Запишем в тетрадях: Дано:
— О каких фигурах идет речь? — Запишем в дано: ∆ АВС и ∆ А₁В₁С₁.	— О треугольниках.
— О равенстве каких элементов говорится в условии?	— О равенстве двух сторон и угла между этими сторонами.
— Выберем эти стороны и найдем угол между этими сторонами. АВ = А₁В₁, АС = А₁С₁, ∠ А = ∠ А₁
— Что нужно доказать?	— Что ∆ АВС = ∆ А₁В₁С₁.
— Запишем: Доказать: ∆ АВС =∆ А₁В₁С₁ — Сделаем чертеж как на экране.
ІІ Исполнительский этап. Нахождение способа доказательства теоремы.
— Каким способом будем доказывать равенство треугольников?	— Методом наложения.
— Запишем: Доказательство (метод наложения) — С чего начнем проводить доказательство? С наложения каких элементов? (Если учащиеся говорят про стороны, то с помощью заготовленных треугольников можно показать, что не всегда такое наложение приведет к совпадению всех элементов треугольника, тогда остается только один вариант, когда доказательство начинаем проводить с наложения равных углов) — Посмотрим на экран, каким образом происходит наложение.
Проведение доказательства теоремы.
— Запишем: 1. Т.к. ∠ А = ∠ А₁, то ∆ АВС можно наложить на ∆ А₁В₁С₁ так, что луч АВ совместится с лучом А₁В₁ и луч АС совместится с лучом А₁С₁.
— Какие элементы треугольника будем потом сравнивать? Что еще дано в условии?	— АВ = А₁В₁
— Что произойдет с точками В и В₁?	— Эти точки совпадут.
— Посмотрим на экран, запишем: 2. Т.к. АВ = А₁В₁, то сторона АВ совместится со стороной А₁В₁ (точка В совместится с точкой В₁).
— О какой стороне еще говорится в условии?	— АC = А₁C₁
— Сделайте вывод о точках С и С₁. — Посмотрим на экран, действительно ли совпадут эти точки?	— Эти точки совпадут.
— Ваше утверждение верно, запишем: 3. Т.к. АC = А₁C₁, то сторона АС совместится со стороной А₁C₁ (точка С совместится с точкой С₁).
— Что произошло с концами отрезков ВС и В₁С₁?	— Концы отрезков ВС и В₁С₁ совпали.
— Что теперь можно сказать про отрезки ВС и В₁С₁?	— ВС = В₁С₁
— Правильно, запишем: 4. Т.к. концы отрезков ВС и В₁С₁ совместились, то сторона ВС совместится со стороной В₁С₁.
— Что произошло с ∆ АВС и ∆ А₁В₁С₁?	— Треугольники совпали, значит они равны.
— Молодцы, запишем: 5. ∆ АВС совместился с ∆ А₁В₁С₁, значит ∆ АВС = ∆ А₁В₁С₁.

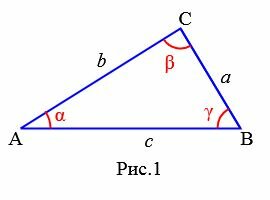Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так &angle;BAC, &angle;ABC, &angle;BCA. Эти же углы коротко обозначают также &angle;A, &angle;B, &angle;C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

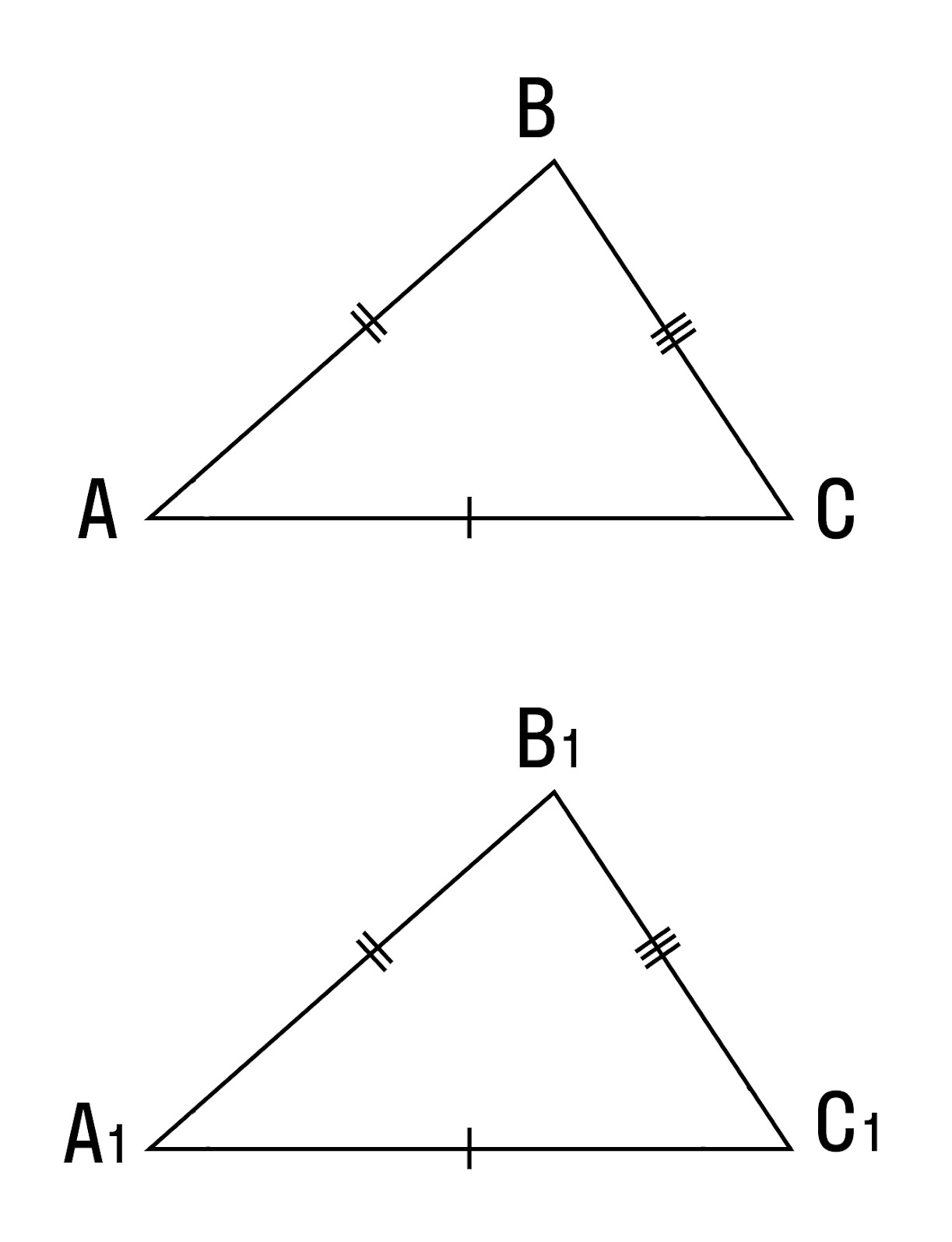
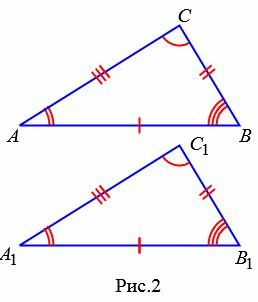
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Видео:Метод наложенияСкачать

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

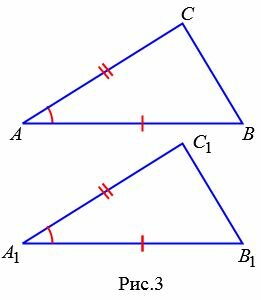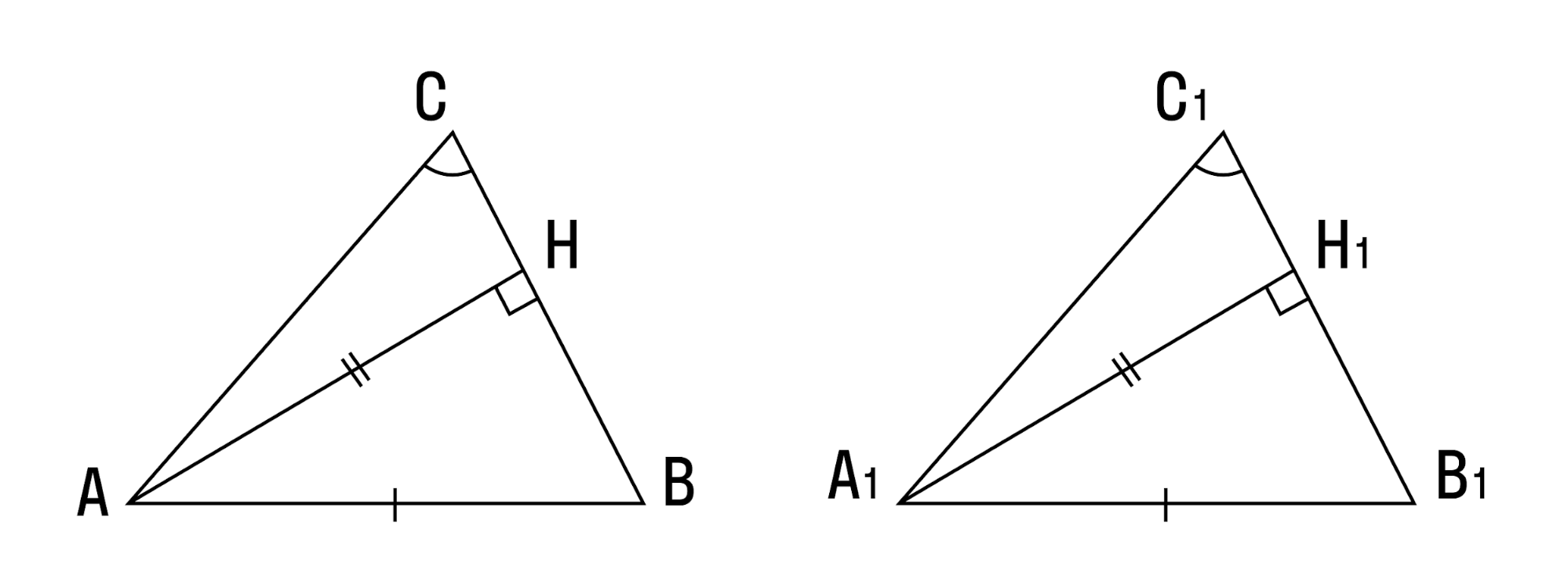
Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и &angle;A=&angle;A₁. Докажем, что .

Видео:Расчет электрических цепей. Метод наложенияСкачать

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

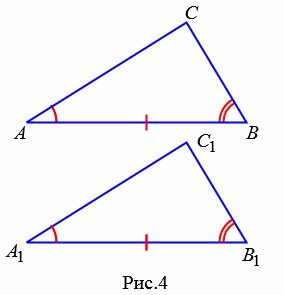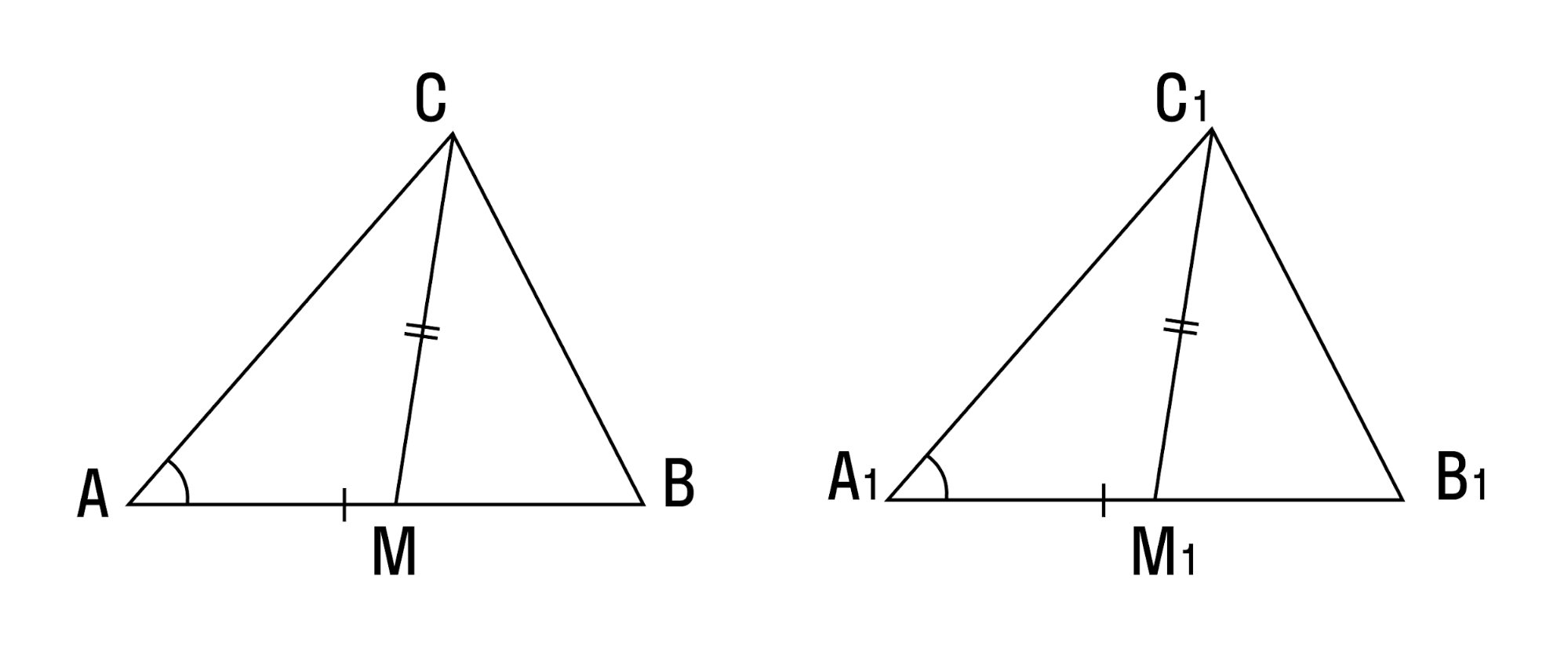
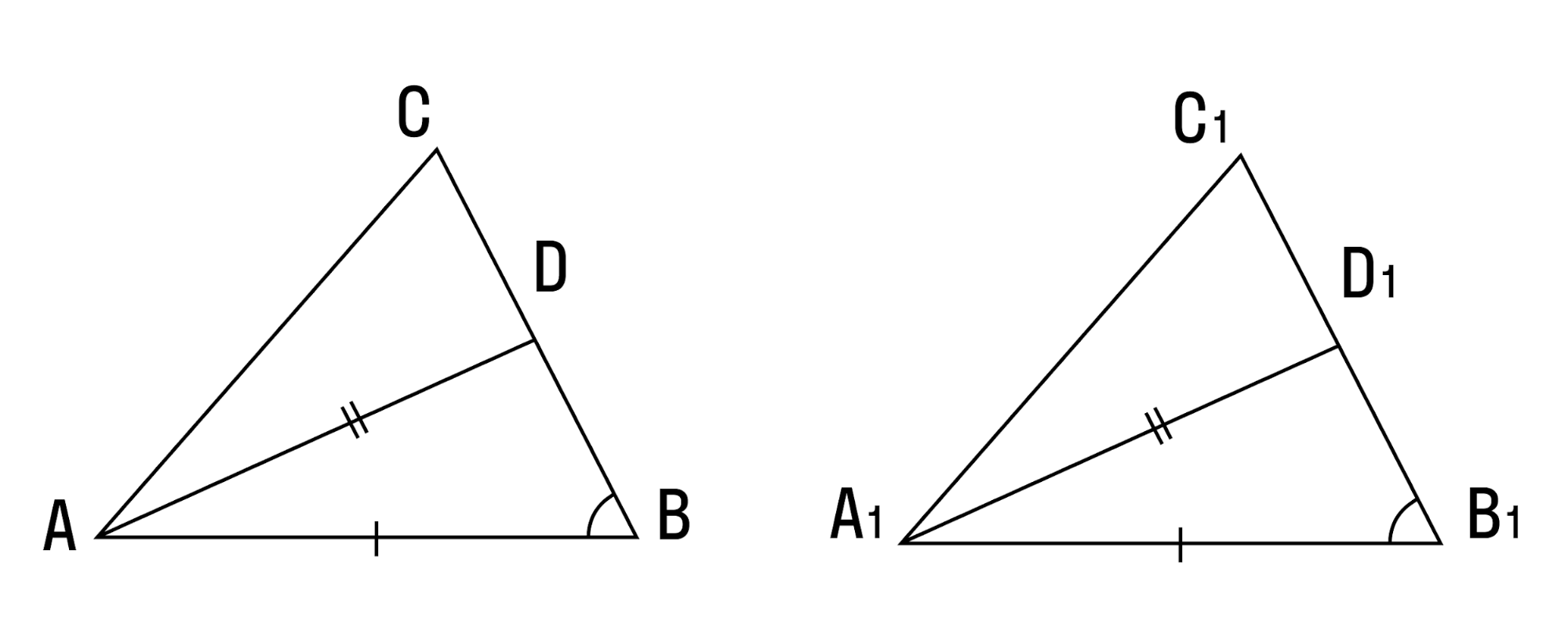
Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, &angle;A=&angle;A₁, &angle;B=&angle;B₁. Докажем, что .

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

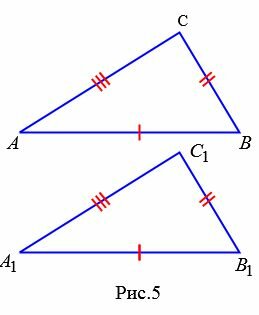Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

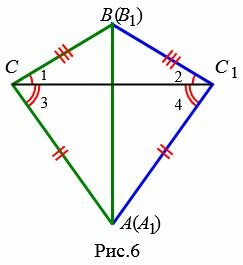Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

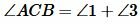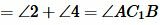Имеем AC=A₁C₁, BC=B₁C₁ &angle;ACB=&angle;A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

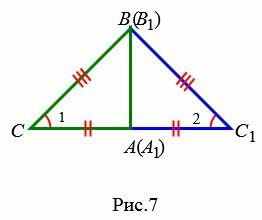Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда &angle;1=&angle;2. Имеем: AC=A₁C₁, BC=B₁C₁, &angle;1=&angle;2 и по первому признаку равенства треугольников . Теорема доказана.

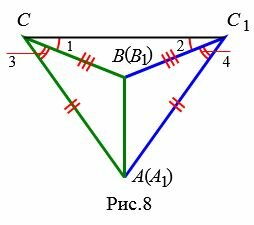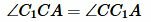
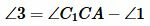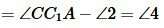Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда &angle;1=&angle;2 и и, следовательно:

Имеем AC=A₁C₁, BC=B₁C₁ 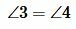и по первому признаку равенства треугольников . Теорема доказана.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что &angle;CBD=&angle;DEC (Рис.9).

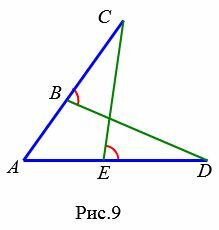Доказательство. AC=AD, AE=AB, &angle;CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно &angle;DBA=&angle;AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−&angle;DBA. Аналогично CED=180°-&angle;AEC. То есть &angle;CBD=&angle;DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, &angle;P=&angle;T

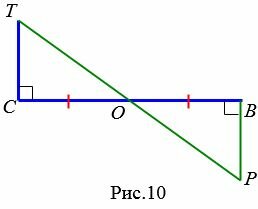Доказательство. OC=OB, &angle;TCO=&angle;PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .