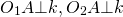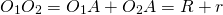Две окружности проходят через центры друг друга (2 видео)

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO₁).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

Пусть окружности O и O₁ имеют общую точку A, лежащую вне линии центров OO_1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO₁.

Опустим из A на прямую OO₁ перпендикуляр AB и продолжим его на расстояние BA₁, равное AB. Докажем теперь, что точка A₁ принадлежит обеим окружностям. Из построения видно, что точки O и O₁ лежат на перпендикуляре, проведенном к отрезку AA₁ через его середину. Из этого следует, что точка O одинаково удалена от A и A₁. То же можно сказать и о точке O₁. Значит обе окружности, при продолжении их, пройдут через A₁.Таким образом, окружности имеют две общие точки : A (по условию) и A₁ (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA₁) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O₁, радиусами R и R₁ и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R₁ .

2. Окружности имеют внешнее касание. Тогда d = R + R₁, так как точка касания лежит на линии центров O O₁.

3. Окружности пересекаются. Тогда d R + R₁, потому что в треугольнике OAO₁ сторона OO₁ меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R₁, потому что точка касания лежит на продолжении линии OO₁.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R₁, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R₁, то окружности касаются извне.

3. Если d R — R₁, то окружности пересекаются.

4. Если d = R — R₁, то окружности касаются изнутри.

5. Если d R Е R₁. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.

Содержание

1. Две окружности, радиусы которых равны r, проходят через центры друг друга?
Из точки окружности проведены две перпендикулярные хорды, разность между длинами которых 4см?
В окружности проведены две взаимно перпендикулярные хорды?
В окружности проведены две взаимно перпендикулярные хорды?
Две взаимно перпендикулярные хорды равной длины пересекаются и в точке пересечения делятся на отрезки 0, 7см и 1, 7см?
В окружности даны две взаимно перпендикулярные хорды, каждая из них делится другой на два отрезка 3 и 7 ?
Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду?
В окружности проведены две взаимно перпендикулярные хорды?
Две окружности с равными радиусами пересекаются в двух точках?
Помогите решить В окружности по разные стороны от ее центра проведены две параллельные хорды, длины которых равны 16 и 32, а расстояние между хордами 16?
В окружности на расстоянии 2 от центра проведены две взаимно перпендикулярные хорды, длина каждой из них равна 8?
Касание двух окружностей
📽️ Видео

Видео:Геометрия Две окружности с центрами O1 и O3 и радиусами 4,5 и 2,5 касаются друг с другом внешнимСкачать

1. Две окружности, радиусы которых равны r, проходят через центры друг друга?

Геометрия | 5 — 9 классы

1. Две окружности, радиусы которых равны r, проходят через центры друг друга.

Выразите r через их общую хорду.

2. Две равные и взаимно перпендикулярные хорды окружности в точке пересечения делятся на части длиной 10 см и 16 см.

Найдите радиус окружности.

Пусть общая хорда AB, O₁иO₂ центры окружностей ; O₁A = O₂A = r , O₁O₂ = r.

ΔO₁A O₂ (такжеΔO₁BO₂) равносторонние со сторонойr.

AB = 2 * (r√3) / 2)⇒r = (AB√3) / 3 .

Пусть AB и CDвзаимно перпендикулярные хорды (AB ⊥ CD) , P_точка пересечения этих хорд (P = [AB]⋂[CD] ) b AP = DP = 10 ; BP = CP = 16 см.

Например , изΔACD : AC / sin∠ADC = 2R⇒R = AC / 2sin∠ADC.

ΔAPC = ΔBPD (по катетам)⇒AC = DB = √(10² + 16²) = 2√(5² + 8²) = 2√89 (см).

ΔAPD равнобедренный прямоугольный треугольник

⇒∠ADP ||∠ADC|| = ∠DAP = 45°.

R = AC / 2sin∠ADC = AC / 2sin45° = (2√89) / (2 * 1 / √2) = √178(см).

Видео:Геометрия Две окружности радиуса R с центрами O1 и O2 касаются друг друга. Их пересекает прямаяСкачать

Из точки окружности проведены две перпендикулярные хорды, разность между длинами которых 4см?

Из точки окружности проведены две перпендикулярные хорды, разность между длинами которых 4см.

Найти хорды, если радиус = 10см.

Видео:Геометрия Две окружности имеют общий центр O (см. рис.). В одной из окружностей проведен диаметр ABСкачать

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Каждая из них делится другой хордой на отрезки, равные 3 и 7.

Найдите расстояниеот центра окружности до каждой из хорд.

Видео:ОГЭ Задание 25 Две окружностиСкачать

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Хорда, длина которой 10 , удалена от центра окружности на расстояние 3.

Найдите длину другой хорды, если известно, что она удалена от центра на расстояние 4.

Видео:ТЕСТ НА ЭРУДИЦИЮ и кругозор: МНОГО УМНЫХ ВОПРОСОВ, ответы знает не каждый. #насколькотыумный #тестСкачать

Две взаимно перпендикулярные хорды равной длины пересекаются и в точке пересечения делятся на отрезки 0, 7см и 1, 7см?

Две взаимно перпендикулярные хорды равной длины пересекаются и в точке пересечения делятся на отрезки 0, 7см и 1, 7см.

Вычислить диаметр окружности.

Видео:ЕГЭ Задание 16 Три окружностиСкачать

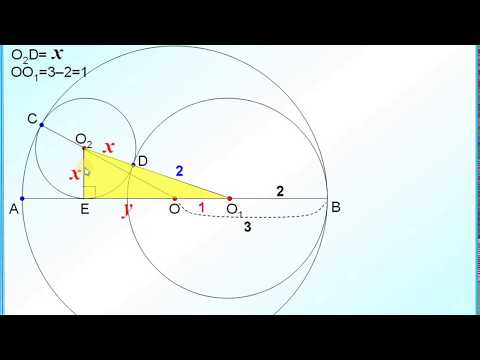
В окружности даны две взаимно перпендикулярные хорды, каждая из них делится другой на два отрезка 3 и 7 ?

В окружности даны две взаимно перпендикулярные хорды, каждая из них делится другой на два отрезка 3 и 7 .

Найдите расстояние от центра окружности до каждой хорды.

Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду?

Две окружности с равными радиусами пересекаются в двух точках, докажите, что отрезок, соединяющий центры окружностей, делит пополам их общую хорду.

Видео:Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

В окружности проведены две взаимно перпендикулярные хорды?

В окружности проведены две взаимно перпендикулярные хорды.

Каждая из них делится другой хордой на отрезки, равные 5 и 11.

Найдите расстояние от центра окружности до точки пересечения хорд.

Видео:Быстро и легко определяем центр любой окружностиСкачать

Две окружности с равными радиусами пересекаются в двух точках?

Две окружности с равными радиусами пересекаются в двух точках.

Докажите, что их общая хорда перпендикулярна к отрезку, соединяющему центры окружностей.

Видео:ЕГЭ Задание 16 Две окружностиСкачать

Помогите решить В окружности по разные стороны от ее центра проведены две параллельные хорды, длины которых равны 16 и 32, а расстояние между хордами 16?

Помогите решить В окружности по разные стороны от ее центра проведены две параллельные хорды, длины которых равны 16 и 32, а расстояние между хордами 16.

Найдите радиус окружности.

Видео:Задание 26 Две окружности, вписанные в угол Внешнее касаниеСкачать

В окружности на расстоянии 2 от центра проведены две взаимно перпендикулярные хорды, длина каждой из них равна 8?

В окружности на расстоянии 2 от центра проведены две взаимно перпендикулярные хорды, длина каждой из них равна 8.

На какие части точка пересечения хорд делит каждую из них?

На этой странице находится вопрос 1. Две окружности, радиусы которых равны r, проходят через центры друг друга?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Высота это прямая делящая противоположную сторону от угла пополам и даёт 90°.

Видео:Планиметрия 11 |mathus.ru| расстояние между центрами пересекающихся окружностейСкачать

Касание двух окружностей

Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.

Общая точка двух окружностей называется точкой касания окружностей.

Касание окружностей может быть внешним и внутренним.

Внешнее касание окружностей — это касание, при котором центры окружностей лежат по разные стороны от общей касательной.

Внутреннее касание окружностей — касание, при котором центры окружностей лежат по одну сторону от общей касательной.

Касающиеся окружности имеют только одну общую точку — точку касания.

Центры касающихся окружностей и их общая точка касания лежат на одной прямой.

При любом виде касания по свойству касательной касательная перпендикулярна радиусам, проведённым в точку касания:

По теореме о существовании и единственности прямой, перпендикулярной данной,через точку A можно провести только одну прямую, перпендикулярную данной прямой k.

Следовательно, все три точки: центры окружностей O1, O2 и A лежат на одной прямой.

Что и требовалось доказать .

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов: