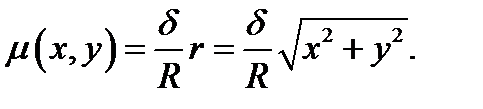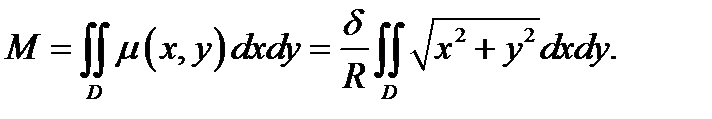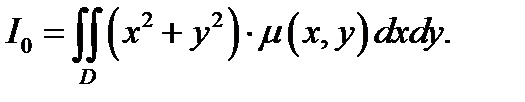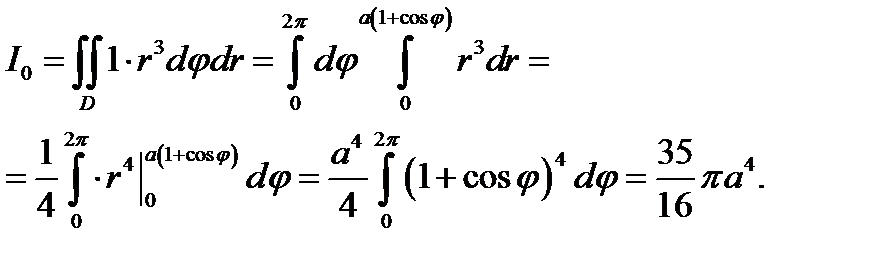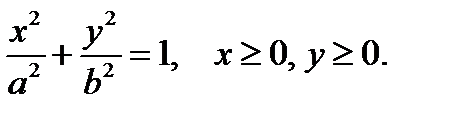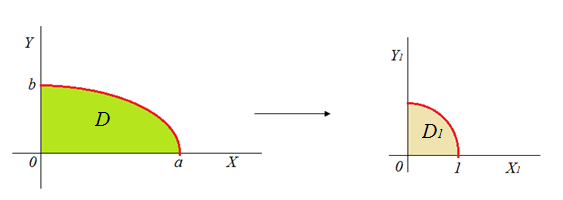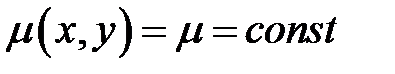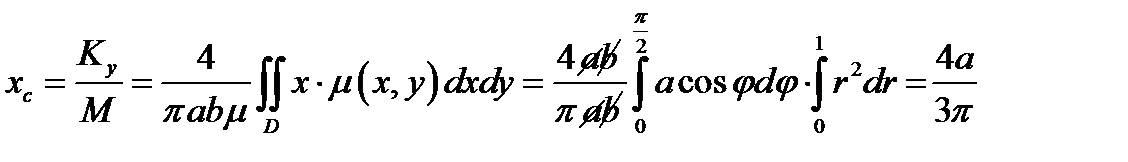Центр масс и моменты инерции кривой;
Работа при перемещении тела в силовом поле;
Магнитное поле вокруг проводника с током (Закон Ампера);
Электромагнитная индукция в замкнутом контуре при изменении магнитного потока (Закон Фарадея).
Рассмотрим эти приложения более подробно с примерами.
Пусть снова кусок проволоки описывается некоторой кривой (C,) а распределение массы вдоль кривой задано непрерывной функцией плотности (rho left( right).) Тогда координаты центра масс кривой определяются формулами [bar x = frac<<<M_>>>,;;bar y = frac<<<M_>>>,;;bar z = frac<<<M_>>>,] где [ <<M_> = intlimits_C <xrho left( right)ds> ,>;; <<M_> = intlimits_C <yrho left( right)ds> ,>;; <<M_> = intlimits_C <zrho left( right)ds> > ] − так называемые моменты первого порядка .
Моменты инерции относительно осей (Ox, Oy) и (Oz) определяются формулами [ <= intlimits_C <left( <+ > right)rho left( right)ds> ,>;; <= intlimits_C <left( <+ > right)rho left( right)ds> ,>;; <= intlimits_C <left( <+ > right)rho left( right)ds> .> ]
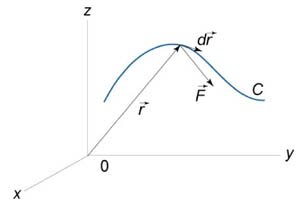
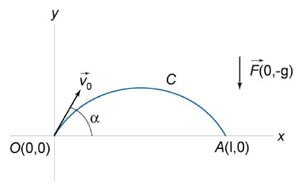
Работа при перемещении тела в силовом поле (mathbf) вдоль кривой (C) выражается через криволинейный интеграл второго рода [W = intlimits_C <mathbfcdot dmathbf> ,] где (mathbf) − сила, действующая на тело, (dmathbf) − единичный касательный вектор (рисунок (1)). Обозначение ( <mathbfcdot dmathbf>) означает скалярное произведение векторов (mathbf) и (dmathbf.)
Заметим, что силовое поле (mathbf) не обязательно является причиной движения тела. Тело может двигаться под действием другой силы. В таком случае работа силы (mathbf) иногда может оказаться отрицательной.
Если векторное поле задано в координатной форме в виде [mathbf = left( <Pleft( right),Qleft( right),Rleft( right)> right),] то работа поля вычисляется по формуле [W = intlimits_C <mathbfcdot dmathbf> = intlimits_C .] В частном случае, когда тело двигается вдоль плоской кривой (C) в плоскости (Oxy,) справедлива формула [W = intlimits_C <mathbfcdot dmathbf> = intlimits_C ,] где (mathbf = left( <Pleft( right),Qleft( right)> right).)
Если векторное поле (mathbf) потенциально , то работа по перемещению тела из точки (A) в точку (B) выражается формулой [W = uleft( B right) — uleft( A right),] где (uleft( right)) − потенциал поля.
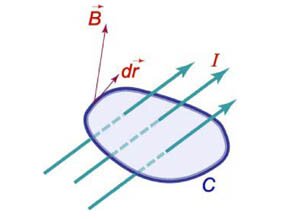
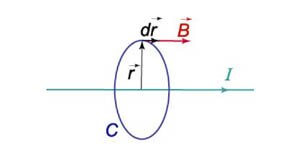
Криволинейный интеграл от магнитного поля с индукцией (mathbf) вдоль замкнутого контура (C) пропорционален полному току, протекающему через область, ограниченную контуром (C) (рисунок (2)). Это выражается формулой [intlimits_C <mathbfcdot dmathbf> = I,] где () − магнитная проницаемость ваккуума , равная (1,26 times <10^>,text.)
Очевидно, в силу симметрии, (bar y = 0.) Чтобы найти координату центра масс (bar x,) достаточно рассмотреть верхнюю половину кардиоиды.
(C) − отрезок прямой (y = x;)
(C) − кривая (y = sqrt x.)
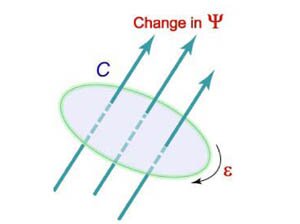
Согласно закону Фарадея [varepsilon = ointlimits_C = — frac<><
Предположим, что магнитное поле (mathbf) перпендикулярно плоскости кольца. Тогда за время (Delta t) изменение потока равно [Delta psi = 2rBx = 2rBvDelta t,] где (x = vDelta t,) (v) − скорость самолета, (B) − индукция магнитного поля Земли. Из последнего выражения получаем [varepsilon = — frac<><
Напряженность возникающего электрического поля найдем по формуле (varepsilon = intlimits_C <mathbfcdot dmathbf> .) В силу симметрии, наведенное электрическое поле будет иметь постоянную амплитуду в любой точке кольца. Оно будет направлено по касательной к кольцу в любой его точке. Это позволяет легко вычислить криволинейный интеграл. [varepsilon = ointlimits_C <mathbfcdot dmathbf> = ointlimits_C = Eointlimits_C = 2pi rE.] Следовательно, напряженность электрического поля равна [E = frac<> = frac<><> = 0,004,text.]
Видео:Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать
Электронная библиотека
Вычисление интеграла (1.4) и (1.5) сводится к определенному. Пусть, например, кривая К задана уравнениями: x = x(t), y = y(t), z = z(t), , тогда длина элементарной дуги , интеграл (1.4) выражается определенным интегралом:
Если, в частности, кривая К имеет явное задание y = y(x) , то
Из соотношения (1.7) и (1.8) следует, что криволинейный интеграл первого рода существует, если f – непрерывная функция на К.
Вычислить по длине плоской кривой y = ln x при .
Решение. Используем формулу (1.8), найдем, что и
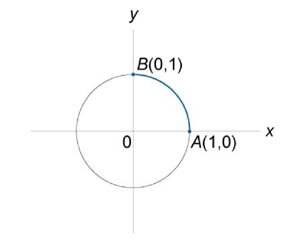
Найти массу полуокружности x 2 + y 2 = 1, , если линейная плотность её в текущей точке M(x,y) пропорциональна ординате y.
Решение. За параметр возьмем величину угла t, тогда параметрическое уравнение линии К: x=cos t, y=sin t .
Элементарная масса dm = ky dl, т.е. тогда по формуле (1.7):
Решение. По формуле (1.7) имеем:
Задачи для упражнений
1) Найти , если К – дуга параболы , лежащая между и . Ответ: .
4) Определить массу окружности x 2 + y 2 = R 2 , если плотность её в точке М(х, у) равна: . Ответ: .
5) Определить координаты центра тяжести С(х0, у0) однородной полуокружности К: .
Указание. В механике доказано, что координаты центра тяжести однородной кривой К задаются формулами:
где L – длина дуги кривой К. Ответ: .
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Видео:Найдите массу дуги окружности ➜ Физический смысл криволинейного интеграла 1-го рода (по длине дуги)Скачать
Момент инерции пластины относительно начала координат. вычисляется по формуле:
вычисляется по формуле:
(4.5)
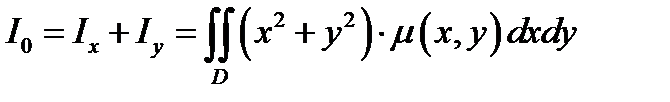
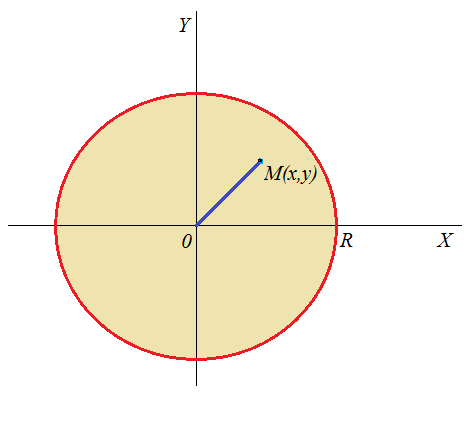
Пример 4.1 . (2225)Найти массу круглой пластинки радиуса R, если плотность в каждой точке пропорциональна расстоянию от центра и равна δ на краю пластинки.
| Рисунок 4.2 |
Из условия следует, что если 
— расстояние от центра до точки, а 
— коэффициент пропорциональности, то плотность 
. При 
. Следовательно, 
, откуда получаем 
. Искомую массу вычисляем по формуле (4.1), подставляя в неё найденную плотность.
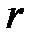
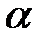
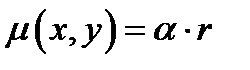
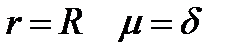
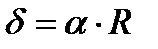
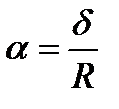
Расставим пределы интегрирования в повторном интеграле, переходя к полярной системе координат, и вычислим его:
.
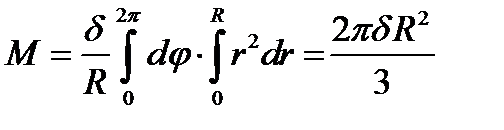
Пример 4.2(2237)
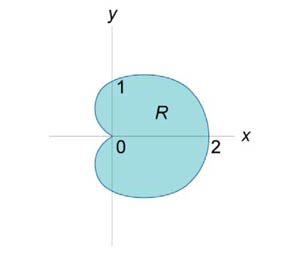
Найдём момент инерции относительно полюса фигуры, ограниченной кардиоидой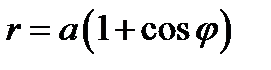 
, если плотность в каждой точке равна единице.
Построим кардиоиду. (См. рис 4.3)
Момент инерции относительно полюса вычислим по формуле (4.5):
При расстановке пределов интегрирования в повторном интеграле перейдём к полярным координатам и затем вычислим интеграл. Получим
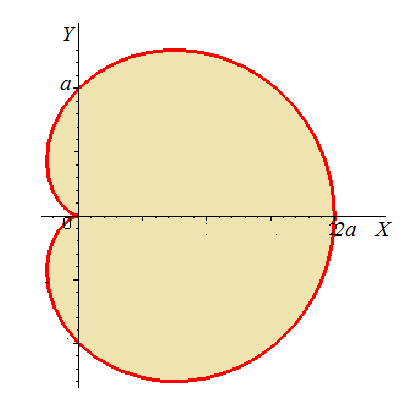
| Рисунок 4.3 |
Пример 4.3. Найдём координаты центра масс однородной пластинки, ограниченной частью эллипса и осями координат так, что 
Решение. Для удобства вычислений перейдём к обобщённым полярным координатам. Для эллипса они имеют вид: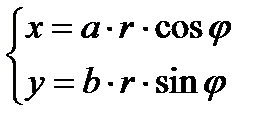 
, 
.
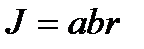
Действительно, при подстановке в уравнение эллипса, имеем:
Таким образом, четверть эллипса отображается в четверть единичной окружности.
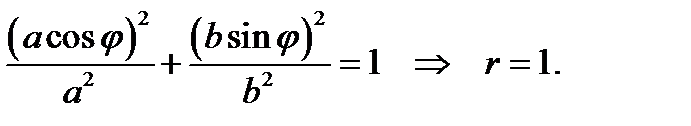
Далее, по формулам (4.1)- (4.3) вычисляем массу пластины, статические моменты и координаты центра масс. Плотность 
.
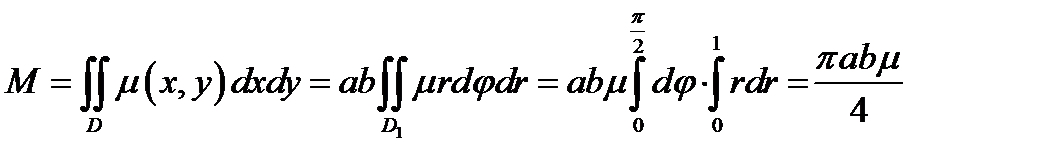
Координаты центра масс:
. Ответ: 
. Домашнее задание к занятию 4:
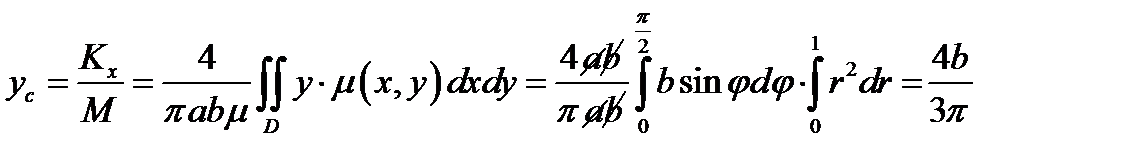
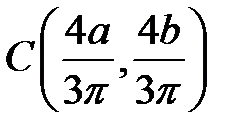
ОЛ-6 №№ 2226, 2229, 2232, 2238 или ОЛ-5 №№ 8.93, 95, 100, 101, 105.
Занятие 5.
Тройной интеграл. Определение тройного интеграла и его свойства. Формулировка теоремы существования тройного интеграла. Сведение тройного интеграла к повторному и его вычисление в декартовой системе координат.
Ауд.: ОЛ-6 №№ 2240, 2242, 2245, 2248, 2249, 2253 или ОЛ-5 №№8.108, 111, 112, 116, 119
📽️ Видео
Как найти массу если известна плотность и объёмСкачать
Масса и измерение массы тел. 7 класс.Скачать
Урок 27 (осн). Плотность. Единицы плотностиСкачать
Плотность вещества | Физика 7 класс #15 | ИнфоурокСкачать
Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать
Физика 7 класс (Урок№10 - Плотность и масса.)Скачать
Масса через двойной интегралСкачать
Масса дугиСкачать
Плотность веществаСкачать
Математический анализ, 41 урок, Вычисление двойных интеграловСкачать
Длина окружности. Математика 6 класс.Скачать
Масса плоской пластины. ОтветыСкачать
Плотность (просто и понятно)Скачать
Урок 30 (осн). Задачи по теме "Плотность" - 2Скачать
Урок 29 (осн). Задачи по теме "Плотность" - 1Скачать
Криволинейный интеграл по длине дуги ➜ Криволинейный интеграл 1-го родаСкачать
Как решают уравнения в России и СШАСкачать
КАК НАЙТИ РАДИУС КРУГА (ОКРУЖНОСТИ), ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать
