Построим произвольную окружность а (4 видео)

Планиметрия (прямая и окружность)

Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).

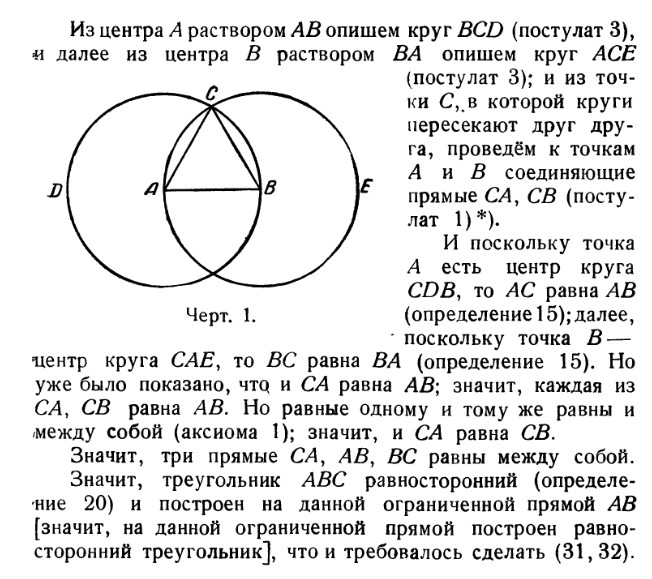
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.

Содержание

1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
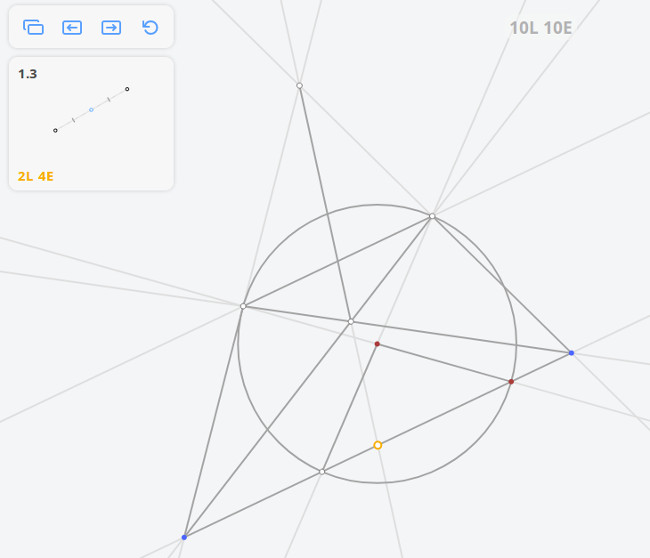
1.3 Середина отрезка
1.4 Окружность, вписанная в квадрат
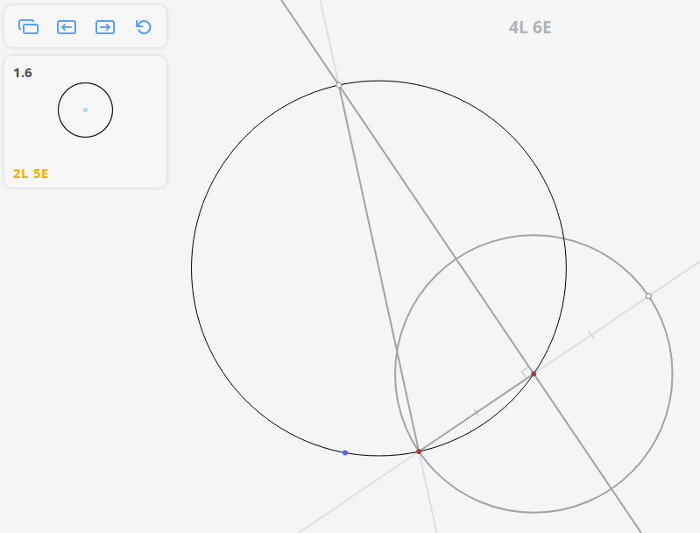
1.6 Найти центр окружности
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Как построить окружность?
Ответы к страницам 106-107 №408-418 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин
Глава 5. Окружность Ответы к параграфу 5.1 Окружность и прямая
Задание № 408
Задание № 409
Задание № 410
Задание № 411
Задание № 412
Задание № 413
Задание № 414
Задание № 415
Задание № 416
Задание № 417
Задание № 418
📸 Видео

1.1 Построить угол 60° с заданой стороной

1.2 Построить серединный перпендикуляр к отрезку

На данной ограниченной прямой построить равносторонний треугольник

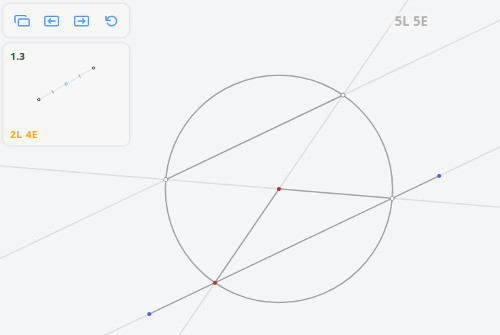
1.3 Середина отрезка

всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.

Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.

любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.

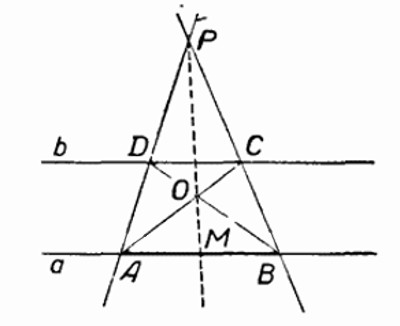
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.

Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат

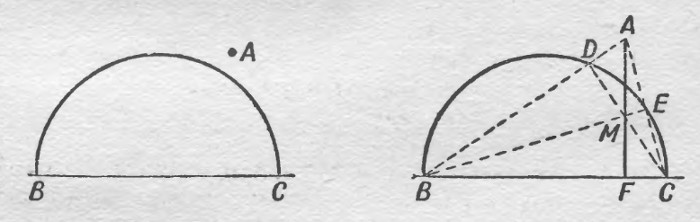
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.

Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.

И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой

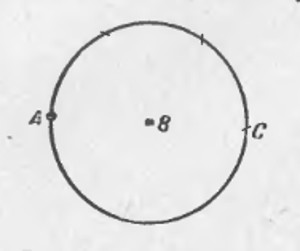
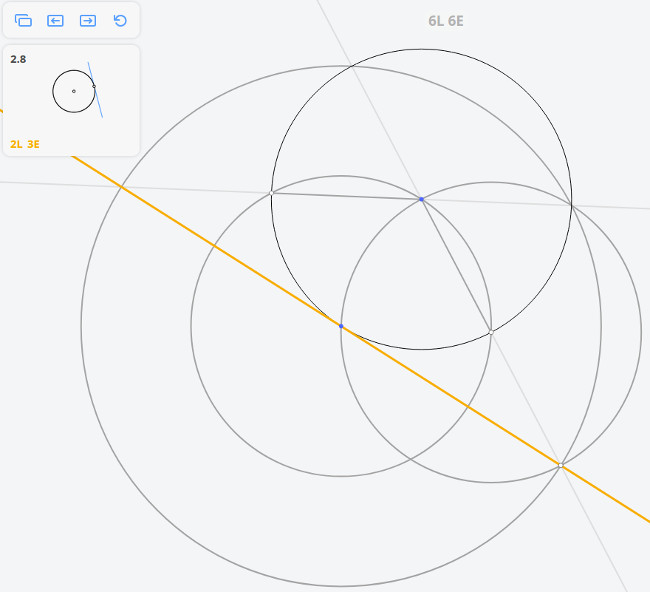
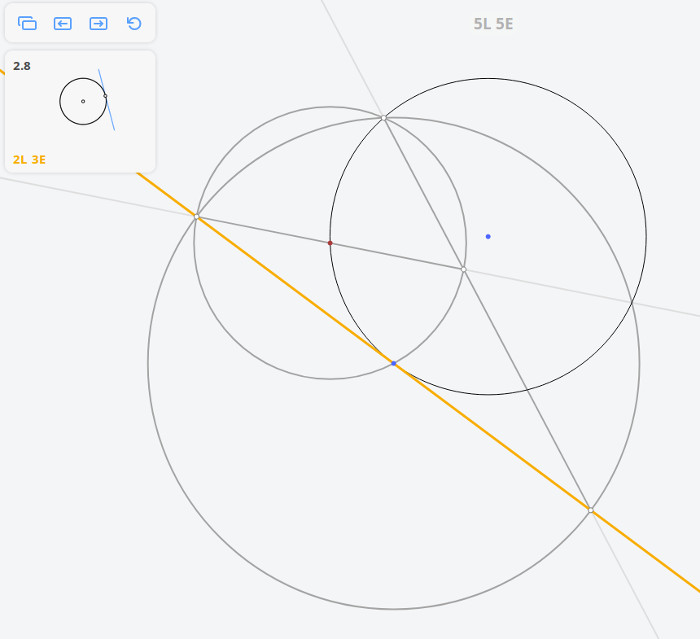
1.6 Найти центр окружности

Плоский угол, опирающийся на диаметр окружности, — прямой.

Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

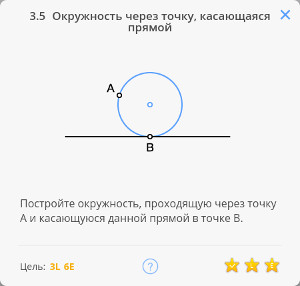
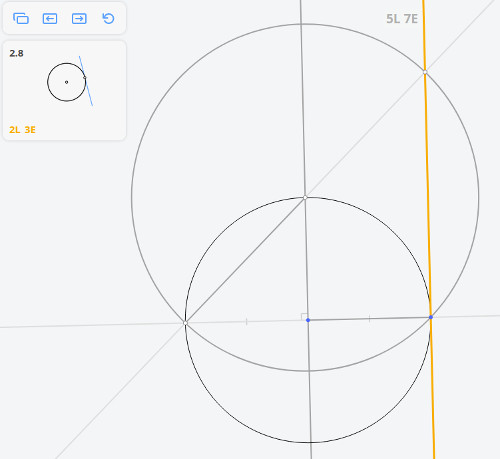
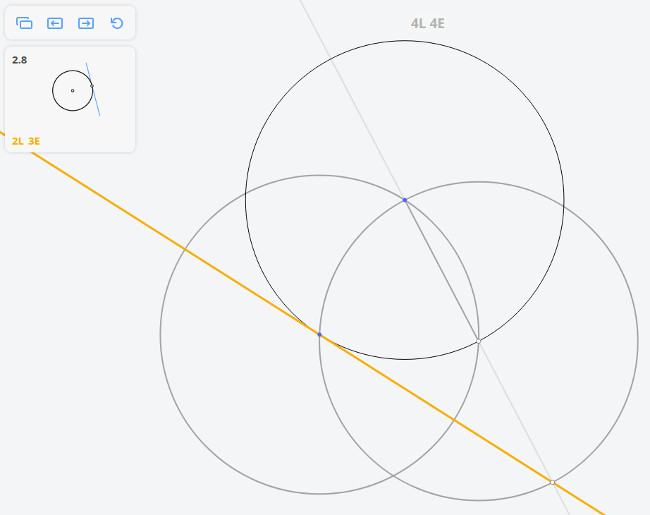
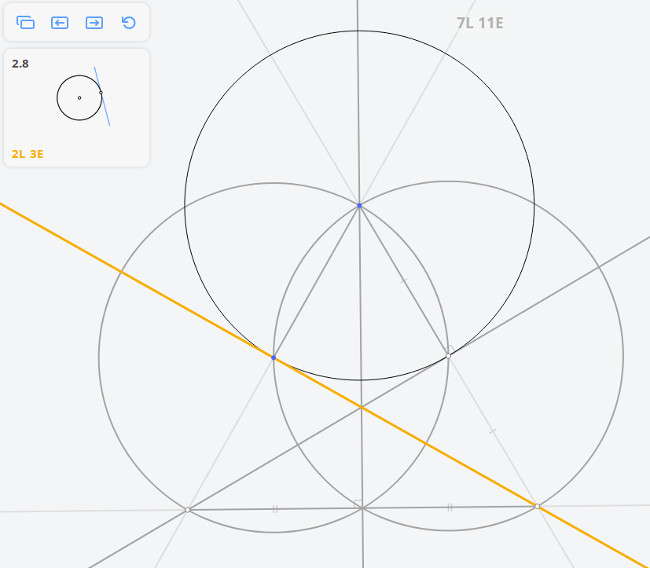
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.

Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка

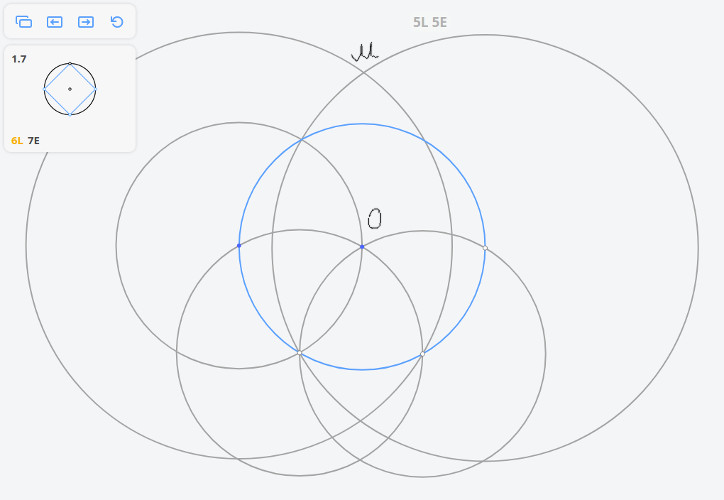
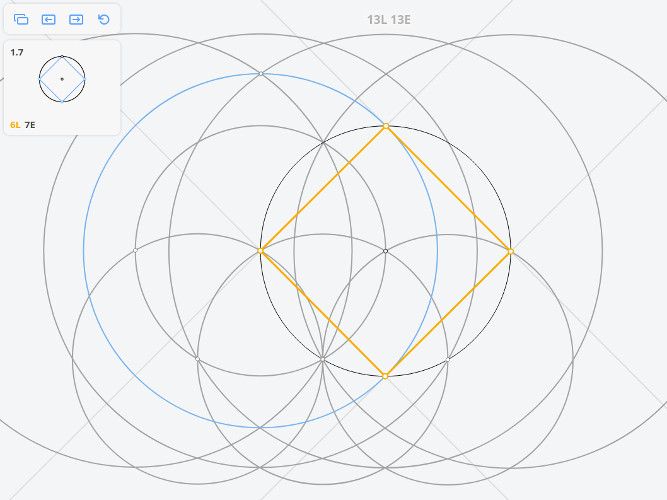
1.7 Квадрат, вписанный в окружность

Задача Наполеона

Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом

В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом

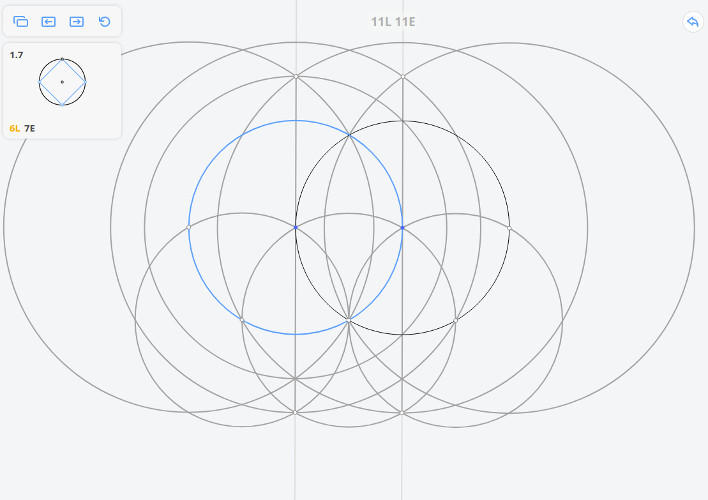
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО

Видео:Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

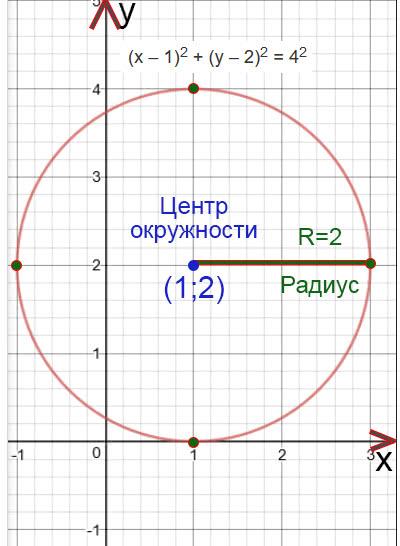
Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Видео:Построить описанную окружность (Задача 1)Скачать

Ответы к страницам 106-107 №408-418 ГДЗ к учебнику «Математика» 6 класс Дорофеев, Шарыгин

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Глава 5. Окружность
Ответы к параграфу 5.1 Окружность и прямая

Задание № 408

Что можно сказать о взаимном расположении прямой и окружности, если расстояние от центра окружности до прямой равно 4 см, а радиус окружности равен:
а) 3 см;
б) 4 см;
в) 6 см?
Подсказка. Сделайте схематический рисунок.

а) Прямая и окружность не имеют общих точек.

б) Прямая и окружность касаются друг друга.

в) Прямая и окружность пересекаются.

Задание № 409

Начертите произвольную окружность и отметьте на ней точку A. Постройте касательную к окружности в точке A.

Задание № 410

К окружности, радиус которой равен 6 см, проведены две параллельные касательные (рис. 5.3). Чему равно расстояние между ними?

6 + 6 = 12 (см) − расстояние между касательными.
Ответ: 12 см.

Задание № 411

Начертите две параллельные прямые. Постройте какую−нибудь окружность, для которой эти прямые являются касательными. Сколько таких окружностей можно построить? Где лежат их центры?

Окружностей можно построить множество. Центры этих окружностей лежат на прямой, параллельной данным и равноудаленной от них.

Задание № 412

Прямая k и окружность пересекается в точках A и B. Прямая k перемещается к центру окружности параллельно самой себе. В какой момент длина отрезка AB будет наибольшей? Сделайте соответствующий рисунок.

Длина отрезка AB будет наибольшей, когда прямая k проходит через центр окружности. В этом случае отрезок AB будет являться диаметром окружности.

Задание № 413

Проведите прямую и постройте какую−нибудь окружность радиусом 3 см, для которой эта прямая являются касательной. Сколько таких окружностей можно построить? Где расположены их центры?

Можно построить бесконечное множество таких окружностей. Их центры будут лежать по обе стороны от данной прямой на прямых, параллельных данной, на расстоянии, равному радиусу окружности 3 см.

Задание № 414

Проведите прямую и отметьте на ней произвольную точку M. Постройте несколько окружностей разных радиусов, касающихся данной прямой в точке M. Где лежат центры всех таких окружностей?

Центры окружностей лежат на прямой, перпендикулярной данной прямой.

Задание № 415

Начертите в тетради квадрат со стороной 8 см. Постройте окружность, касающуюся всех сторон квадрата.

Задание № 416

Представьте данное число в виде произведения двух десятичных дробей (укажите два решения):
а) 0,12;
б) 0,064;
в) 0,0002;
г) 0,3.

б) 0,064 = 0,4 * 0,16 = 0,8 * 0,08

в) 0,0002 = 0,1 * 0,002 = 0,001 * 0,2

Задание № 417

Найдите значение каждого из выражений:
1) 25 − 3,6 * 1,5 + 2,5;
2) (25 − 3,6) * (1,5 + 2,5);
3) 25 − 3,6 * (1,5 + 2,5).

Задание № 418

1) В полиэтиленовый пакет, выдерживающий 5 кг, положили 1,8 кг огурцов, а яблок в 1,5 раза больше. Не порвется ли пакет?
2) Представьте, что вы хотите помочь бабушке подготовить материал для изготовления шерстяного ковра из ниток разного цвета. Чтобы получить нужный узор, 1/10 всех ниток должна быть красного цвета, 2/5 − синего, 3/20 − коричневого, остальные − белого. У бабушки имеется 700 г ниток белого цвета. Рассчитайте, сколько граммов ниток каждого цвета надо взять для выполнения работы.