Плоскость колебаний электрического вектора

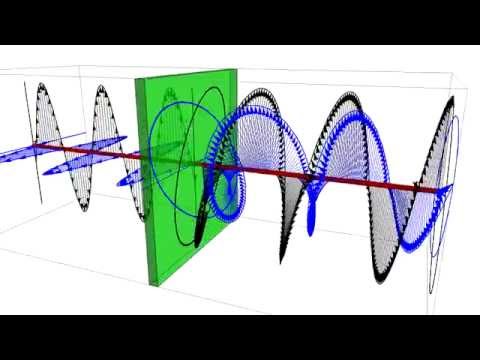
Следствием теории Максвелла является поперечность электромагнитных (световых) волн распространяющихся в вакууме или изотропной среде: векторы напряженности электрического и магнитного полей волны взаимно перпендикулярны и колеблются перпендикулярно вектору скорости v распространения волны (то есть перпендикулярно световому лучу). Явление поляризации света служит надежным обоснованием поперечности световой волны. При рассмотрении поляризации обычно все рассуждения связывают с плоскостью колебаний вектора напряженности электрического поля Е — светового вектора, так как химическое, физиологическое и другие виды воздействия света на вещество обусловлены главным образом электрическими колебаниями. Однако при этом следует помнить об обязательном существовании перпендикулярного ему вектора напряженности магнитного поля Н.

Поляризация электромагнитной волны. Записывая решение для электрического поля плоской электромагнитной волны в виде

мы предполагали, что направление вектора амплитуды колебаний не зависит от времени. В этом случае вектор электрического поля всегда и во всех точках волны направлен вдоль одной и той же прямой — колеблется в одной плоскости неизменной ориентации в пространстве.

Плоскость, в которой происходят колебания светового вектора, то есть плоскость, содержащая вектор 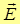и направление распространения волны, называется плоскостью колебаний. Если эта плоскость не меняет во времени своей ориентации, то волна называется — линейно (плоско) поляризованной.

Выбирая ось х вдоль направления распространения волны, а ось у — вдоль векторной амплитуды 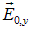, записываем (6.1) в виде

Однако существует и вторая линейно поляризованная волна, имеющая ту же частоту и распространяющаяся в том же направлении:

Электрические колебания в этой волне направлены вдоль оси z, так что волны (6.2) и (6.3) линейно независимы. Обе они являются решением одного и того же волнового уравнения, так что их суперпозиция также является решением того же уравнения. Сложив эти волны, мы найдем общее выражение для монохроматической волны с данной частотой w, распространяющейся вдоль оси х. Математически эта процедура ничем не отличается от сложения взаимно ортогональных колебаний. Если зафиксировать какую-то точку х и следить за изменением вектора электрического поля в ней, то конец вектора будет описывать эллиптическую, в общем случае, траекторию в плоскости, параллельной y0z. Вращение вектора происходит с частотой волны . В этом случае говорят, что свет имеет эллиптическую поляризацию. Если разность фаз кратна , то эллиптическая поляризация вырождается в линейную. При равенстве амплитуд Е_0,у и Е_0,г эллипс превращается в окружность. Тогда говорят о круговой поляризации волны. В соответствии с двумя возможными направлениями вращения вектора возможны право- и левополяризованные волны. Любую электромагнитную волну можно представить как линейную комбинацию двух линейно поляризованных волн или как линейную комбинацию двух волн с круговой поляризацией. Иными словами, электромагнитные волны имеют две внутренние степени свободы.

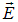
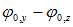
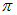
Естественный и поляризованный свет. В свете, испускаемом обычными источниками, имеются колебания, совершающиеся в различных направлениях, перпендикулярных к лучу. В таких световых волнах, исходящих из различных элементарных излучателей (атомов), векторы имеют различные ориентации, причем все эти ориентации равновероятны, что обусловлено большим числом атомных излучателей. Такой свет называется естественным, или неполяризованным.

Если под влиянием внешних воздействий на свет или внутренних особенностей источника света (лазер) появляется предпочтительное, наиболее вероятное направление колебаний, то такой свет называется частично поляризованным. Неполяризованный (естественный) свет может испускаться лишь огромным числом элементарных излучателей. Электромагнитная волна от отдельного элементарного излучателя (атома, молекулы) всегда поляризована. С помощью различных поляризаторов из пучка естественного света можно выделить часть, в которой колебания вектора 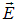будут происходить в одном определенном направлении в плоскости, перпендикулярной лучу, то есть выделенный свет будет линейно поляризованным.

На рисунках направление колебаний электрического поля линейно поляризованной волны изображается следующим образом. Если вектор Е колеблется в плоскости чертежа, то на направление вектора скорости волны 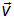наносится ряд вертикальных стрелочек (рис. 6.1-1), а если в плоскости, перпендикулярной чертежу, — ряд точек (рис. 6.1-2). Естественный (неполяризованный) свет условно обозначается чередующимися черточками, которым соответствует, например, компонента Е_y вектора напряженности электрического поля, и точками, соответствующими другой компоненте Е_z (рис. 6.1-3).

Рис. 6.1. Условные обозначения типа поляризации волны

Существуют приборы (поляризаторы), пропускающие только колебания, происходящие параллельно некоторой плоскости, называемой плоскостью поляризации прибора, и полностью задерживающие ортогональные колебания. Если пропустить через такой прибор пучок света, то на выходе он будет линейно поляризованным. При вращении прибора вокруг направления луча интенсивность выходящего света будет изменяться от I_MAX до I_MIN.

Степень поляризации света — это величина

Отметим, что формула (6.4) пригодна для расчета степени поляризации света лишь в том случае, когда частично поляризованный свет представляет собой смесь естественного света и света линейно поляризованного и не работает, например, в случае смеси естественного света и света поляризованного по кругу. В общем случае степень поляризации может быть рассчитана как отношение интенсивности поляризованной компоненты к суммарной интенсивности волны, то есть сумме интенсивностей поляризованной и естественной компонент смеси:

Нетрудно показать, что (6.4) есть частный случай последней формулы.

Если падающий пучок света линейно поляризован, то при положении прибора, когда его плоскость поляризации ортогональна плоскости колебаний волны, свет через прибор не пройдет, то есть . В соответствии с формулой (6.4) степень поляризации такого света . Для частично поляризованного света

и . Для естественного света, где волны разных поляризаций смешаны в равной степени и все направления эквивалентны, интенсивность выходящего света не изменяется при вращении поляризатора, так что и .

Закон Малюса. В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора Е, например природные кристаллы турмалина. Монокристалл турмалина поглощает колебания вектора Е в одном направлении настолько сильно, что сквозь пластинку толщиной порядка 1 мм проходит только линейно поляризованный луч. Кристаллы йодистого хинина еще сильнее поглощают одну из поляризаций: кристаллическая пленка толщиной в десятую долю миллиметра практически полностью отделяет один из линейно поляризованных лучей.

Пусть естественный свет распространяется перпендикулярно плоскости рисунка 6.2.

Рис. 6.2. Разложение вектора амплитуды колебаний А в волне, падающей на поляризатор

Вектор амплитуды колебаний электрического поля волны, совершающихся в плоскости, образующей с плоскостью поляризатора угол , можно разложить на два колебания с амплитудами

Первое колебание с амплитудой А_|| пройдет через прибор (поляризатор), второе — с амплитудой А — будет задержано (поглощено). Интенсивность прошедшей волны пропорциональна квадрату амплитуды

Падающая волна является смесью волн с различными углами . Усредняя по углам, получаем для интенсивности света на выходе из поляризатора:

где — интенсивность падающего на поляризатор света. В естественном свете все значения угла равновероятны:

так что интенсивность света, прошедшего через поляризатор, будет равна . При вращении поляризатора вокруг направления луча естественного света интенсивность прошедшего света остается неизменной, но изменяется лишь ориентация плоскости колебаний света, выходящего из прибора.

Рассмотрим теперь падение линейно поляризованного света с интенсивностью на тот же поляризатор (рис. 6.3).

Рис. 6.3. Прохождение линейно поляризованной волны через поляризатор

Сквозь прибор пройдет составляющая колебаний с амплитудой

где — угол между плоскостью колебаний вектора Е и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением

которое носит название закона Малюса.

Поляризационные приборы по своему целевому назначению делятся на поляризаторы и анализаторы. Поляризаторы служат для получения поляризованного света. С помощью анализатора можно убедиться, что падающий свет поляризован, и выяснить направление плоскости поляризации. Принципиальных различий в конструкционном отношении между поляризатором и анализатором не существует.

Поставим на пути естественного света два поляризатора, плоскости которых образуют угол (рис. 6.4).

Рис. 6.4. Пропускание естественного света через систему из двух поляризаторов

Из первого поляризатора выйдет линейно поляризованный свет, интенсивность которого , составит половину интенсивности падающего естественного света . Согласно закону Малюса из второго поляризатора (который играет роль анализатора) выйдет свет с интенсивностью

Таким образом, интенсивность света, прошедшего через два поляризатора, равна

Если угол (плоскости поляризации поляризатора и анализатора параллельны), то ; если (анализатор и поляризатор скрещены), то .

Пример 1. В частично поляризованном свете амплитуда колебаний, соответствующая максимальной интенсивности света при прохождении через поляризатор, в n = 2 раза больше амплитуды, соответствующей минимальной интенсивности. Определим степень поляризации света.

Поскольку интенсивность пропорциональна квадрату амплитуды, имеем

Отсюда степень поляризации света равна

Пример 2. На пути света со степенью поляризации Р = 0.6 поставили анализатор так, что интенсивность прошедшего света стала максимальной. Определим, во сколько раз уменьшится интенсивность, если анализатор повернуть на угол ?

В падающем луче по условию (см. предыдущий пример)

При повороте анализатора на угол будут пропущены колебания, параллельные плоскости поляризации прибора. Поэтому интенсивность пропущенных колебаний, прежде бывших параллельными плоскости поляризации, составит

a интенсивность прошедших колебаний, до поворота задерживавшихся анализатором, равна

Суммарная интенсивность прошедших колебаний равна сумме

Стало быть, интенсивность уменьшится при повороте анализатора в 16/13 = 1.23 раза.

Поляризация при отражении и преломлении. Получить поляризованный свет из естественного можно еще одним способом — отражением. Опыт показывает, что отраженный от поверхности диэлектрика и преломленный лучи всегда частично поляризованы. Когда свет падает на диэлектрическую поверхность, то в отраженном луче преобладают колебания, перпендикулярные плоскости падения (точки на рис. 6.5), а в преломленном луче — колебания, параллельные плоскости падения (стрелки на рис. 6.5).

Рис. 6.5. Поляризация света при отражении и преломлении

Степень поляризации зависит от угла падения лучей и от относительного показателя преломления сред. Исследуя это явление, английский физик Д. Брюстер установил, что при определенном значении угла падения

отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча. Это соотношение известно как закон Брюстера. При

отражается только та компонента вектора напряженности электрического поля, которая параллельна поверхности диэлектрика (перпендикулярна плоскости падения). Соответственно, преломленный луч всегда частично поляризован, так как отражается лишь какая-то доля падающего света (не равная 50 %).

При падении света под углом Брюстера отраженный и преломленный лучи взаимно перпендикулярны, отраженный свет полностью поляризован в плоскости, перпендикулярной плоскости падения луча, а преломленный луч частично поляризован с максимальной степенью поляризации.

находим с учетом закона преломления

откуда следует, что преломленный луч 0С перпендикулярен отраженному лучу 0В (рис. 6.6).

Рис.6.6. Ход лучей при падении света под углом Брюстера: отраженный луч ортогонален преломленному,
поэтому излучатели типа (см. текст ниже) не вносят вклад в поляризацию отраженного луча

Для того чтобы объяснить, почему отраженный при падении под углом Брюстера луч линейно поляризован в плоскости, перпендикулярной плоскости падения, учтем, что отраженный свет есть результат излучения вторичных волн колеблющимися под действием светового вектора волны электрическими зарядами (электронами) в среде II. Эти колебания происходят в направлении колебаний вектора Е.

Разложим колебания вектора Е в среде II на два взаимно перпендикулярных направления (см. рис. 6.6): колебания , происходящие в плоскости падения (показаны стрелками), и колебания , происходящие перпендикулярно плоскости падения (показаны точками). В случае падения под углом Брюстера

отраженный луч 0В перпендикулярен преломленному лучу 0С. Следовательно, 0В параллелен 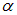. Из электромагнитной теории Максвелла известно, что колеблющийся электрический заряд не излучает электромагнитных волн вдоль направления своего движения. Поэтому колеблющийся в диэлектрике излучатель типа вдоль направления 0В не излучает. Таким образом, по направлению отраженного луча 0В распространяется свет, посылаемый только излучателями типа , направления колебаний которых перпендикулярны плоскости падения.

Следует отметить, что на опыте закон Брюстера не выполняется вполне строго из-за дисперсии света.

Пример 3. Определим, на какой угловой высоте над горизонтом должно находиться Солнце, чтобы солнечный свет, отраженный от поверхности воды, был полностью поляризован.

Угол падения света связан с высотой Солнца над горизонтом соотношением

По условию угол падения равен углу Брюстера, так что

Показатели преломления воды п₂ = 1.33, воздуха — п₁ = 1. Отсюда находим

Пример 4. Угол Брюстера при падении света из воздуха на кристалл каменной соли равен . Определим скорость света V в этом кристалле.

Поскольку показатель преломления воздуха равен единице, показатель преломления каменной соли п совпадает с относительным показателем преломления этих двух сред. Имеем поэтому

Видео:Поляризация света и закон МалюсаСкачать

Поляризация света простыми словами: что это такое, типы, примеры

Если свободный конец веревки, привязанной к устойчивому объекту, регулярно «помахивать», то на ней образуется поперечная волна. Она может быть колеблющейся в одной плоскости — вертикальной, горизонтальной или под определенным углом к горизонтали. Такая волна называется поляризованной. Если веревка вибрирует неравномерно, в разных плоскостях, через нее будет распространяться неполяризованная волна. Свет, который является электромагнитной волной, ведет себя подобно волне на веревке. Это свойство используется, например, в 3D-очках для различения изображения для левого и правого глаза.

Поперечная волна называется плоскополяризованной, eсли колебания во всех ее точках происходят только в одной плоскости.

Применительно к свету термин поляризация ввел в 1704-1706 г. Ньютон.

Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Поляризованная световая волна

Свет — это волна электромагнитного излучения, т.е. возмущение электрического и магнитного поля, перемещающегося в пространстве. Для простоты мы будем говорить о монохроматическом свете, то есть о гармонической волне с определенной частотой и длиной волны.

Электромагнитная волна — это поперечная волна. Это означает, что его электрическое поле E всегда перпендикулярно (колеблется перпендикулярно) направлению распространения волны. Мы говорим, что волна поляризована, если электрическое поле в любой точке имеет одинаковое направление. Пример поляризованной волны показан на рисунке 1.

Итак, поляризация света описывает направление колебаний вектора электрического поля.

Поляризованная волна (от англ. polarized wave) — волна, электрическое поле которой колеблется в одной плоскости.

Рис. 1. Поляризованная волна

Волна, показанная на рис. 1, колеблется в вертикальном направлении. Направление колебаний поляризованной волны называется направлением поляризации. Это направление может быть любым — волна может колебаться вертикально (рис. 2. b), горизонтально (рис. 2. a) или под определенным углом (рис. 2. c).

Рис. 2. Волны с различными направлениями поляризации

Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Неполяризованная волна

Не все волны поляризованы. В некоторых волнах направление электрического поля хаотично меняется от места к месту. Такая волна называется неполяризованной (рис. 3).

Рис. 3. Неполяризованная волна

Такова природа света, излучаемого нагретым металлом, например, вольфрамовой нитью обычной лампочки. Свет, излучаемый светящимся атомарным газом, например, неоновой лампой (светятся атомы неона) или пламенем газовой горелки с соляным раствором (светятся атомы натрия), также неполяризован.

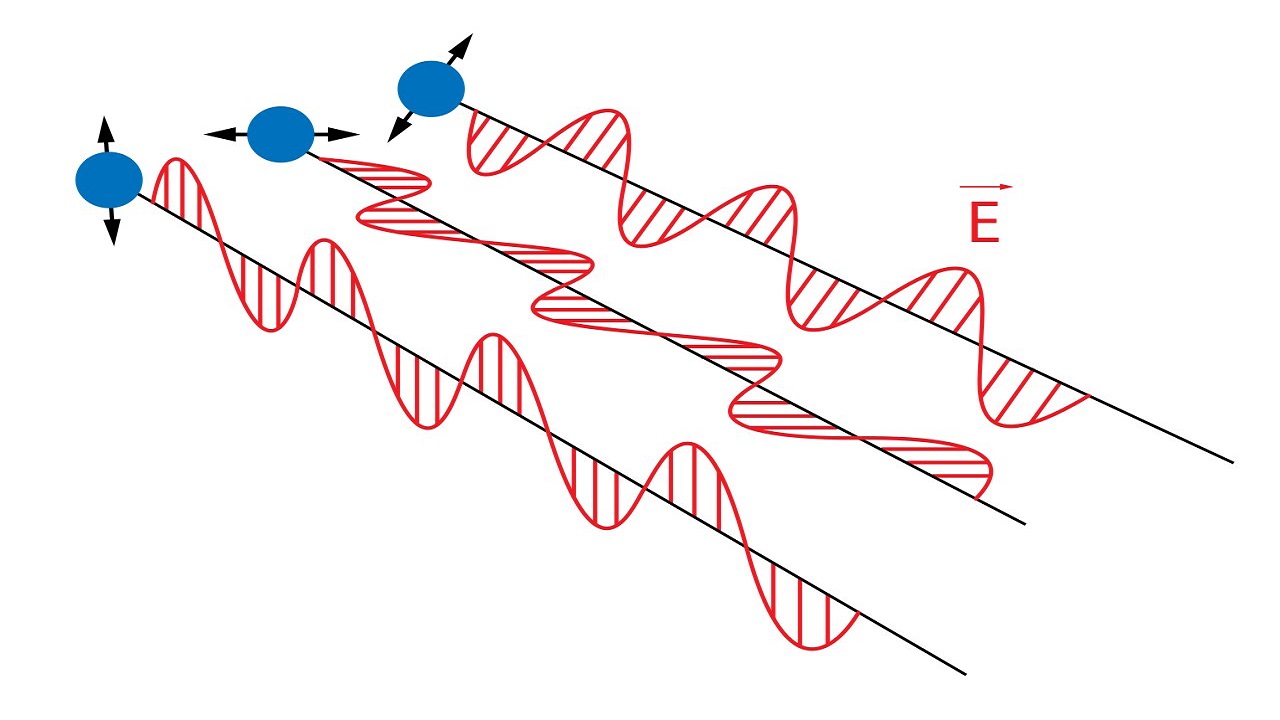
Используя последний пример, мы объясним, почему эти волны неполяризованы. В результате нагревания тела атомы начинают вибрировать и светиться, чтобы избавиться от избытка энергии. Направления колебаний этих атомов случайны, и поэтому направление электрического поля излучаемой электромагнитной волны также изменяется случайным образом. На рис. 4 мы видим три атома, которые являются источником волн с разной поляризацией. Результатом их объединения является неполяризованная волна.

Рис. 4. Колеблющиеся атомы являются источником волн с различной поляризацией

Видео:Урок 336. Векторное представление колебанийСкачать

Разложение любой волны на две поляризованные волны

Каждая волна может быть разложена на две поляризованные волны с произвольно выбранными перпендикулярными направлениями электрического поля. Это следует из простого факта: каждый вектор на плоскости может быть представлен как сумма двух векторов, перпендикулярных друг другу. Это относится как к поляризованным, так и к неполяризованным волнам.

Такое разложение поляризованной волны с «любым» направлением поляризации на волну с вертикальным электрическим полем (зеленая волна) и горизонтальным электрическим полем (красная волна) показано на рис. 5.

Рис. 5. Разложение поляризованной волны с «любым» направлением поляризации на волну с вертикальным электрическим полем (зеленая волна) и горизонтальным электрическим полем (красная волна)

Видео:Математика это не ИсламСкачать

Поляризатор

Поляризатор — это устройство, которое из падающего неполяризованного света пропускает только те электромагнитные волны, электрический вектор которых лежит в направлении, заданном поляризатором.

Система, называемая поляризатором, работает следующим образом. У него есть определенная направленность. На рис. 6 это горизонтальное направление.

1. Если на поляризатор падает поляризованная волна, в которой направление электрического поля совпадает с направлением выделенной волны, то она проходит через него без изменения амплитуды (рис. 6. a).
2. Если на него падает поляризованная волна, в которой направление электрического поля перпендикулярно выделенному направлению, то она вообще не проходит (рис. 6. b).
3. Если на него падает поляризованная волна, у которой направление поляризации образует ненулевой угол с выделяемым направлением, то проходит только ее составляющая вдоль выделяемого направления (рис. 6. c и 6. d). Пройдя через него, волна, очевидно, становится поляризованной.
4. Если на поляризатор падает неполяризованная волна, то через него проходит только ее составляющая вдоль выделенного направления. Очевидно, что это поляризованная волна. Таким образом, поляризатор преобразует неполяризованную волну в поляризованную.

Рис. 6. Через поляризатор проходит только составляющая напряженности электрического поля в выделенном направлении — здесь горизонтальном.

В настоящее время для поляризации света обычно используются специальные пластиковые пленки, называемые поляризационными фильтрами. Такие пленки используются в компьютерных мониторах.

Поляризационный фильтр (от англ. polarizing filter) — широко известен как поляроид; прозрачная пластина или пленка, которая действует как поляризатор, т.е. устройство, которое из падающего неполяризованного света пропускает только те электромагнитные волны, электрический вектор которых лежит в направлении, указанном поляризатором.

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Частично поляризованный свет

Есть и другая возможность. Электрические поля световой волны принимают все возможные направления, но вероятность их возникновения неодинакова. Для определенного направления он наибольший, а для перпендикулярного ему направления — наименьший. Когда мы исследуем такой свет с помощью вращающегося поляризатора, мы получаем результат, показанный на рис. 7. Мы говорим о таком свете, что он частично поляризован.

Рис. 7. График зависимости интенсивности света от угла поворота поляризатора, полученный при испытании частично поляризованного света.

Видео:Геометрия. 9 класс. Векторы на плоскости /27.10.2020/Скачать

Поляризация света при отражении

В повседневной жизни мы постоянно наблюдаем прохождение света через стеклопакеты. Мы видим, что обычно свет попадает в стекло и отражается от его поверхности одновременно. Однако оказалось, что при правильном выборе источника света и угла наклона свет может вообще не отражаться. Это определяется поляризацией световой волны.

Предположим, что луч поляризованного света падает на поверхность двух сред под углом α ≠ 0⁰. Плоскость, содержащая падающий луч и нормаль, называется плоскостью падения. На рисунке 8 эта плоскость обозначена синим цветом.

Когда мы рассматриваем падение поляризованного света на поверхность, то должны различать два основных случая. Они показаны на рис. 8. В обоих случаях луч света движется по прямой линии x:

• a. Электрическое поле (красные векторы) электромагнитной волны перпендикулярно плоскости падения (синяя плоскость),
• b. Электрическое поле E гармонической электромагнитной волны параллельно плоскости падения (красные векторы лежат на синей плоскости). Затем это поле образует угол α с границей среды. Этот угол также лежит в плоскости падения (синяя плоскость).

Рис. 8. Волна, падающая на поверхность

Было исследовано, как зависит величина электрического поля отраженного света от угла падения для вещества с показателем преломления n в этих ситуациях. На рис. 9 показано отношение величины амплитуды электрического поля отраженного света к амплитуде падающего света E₀ при прохождении света из воздуха в среду с показателем преломления n=1,5 в зависимости от угла падения. Таким материалом является, например, стекло.

Рис. 9. Отношение величины амплитуды электрического поля отраженного света к амплитуде падающего света в зависимости от угла падения.

a. Синяя кривая соответствует поляризации (a) на рис. 8. Для перпендикулярного падения, т.е. α = 0⁰, отношение E/E₀ равно 0,2. По мере увеличения угла α увеличивается величина E/E₀. Это означает, что все большая часть падающего света отражается, а не преломляется. Отношение E/E₀ достигает 1 при значениях угла α, приближающихся к 90°. Тогда весь свет отражается.

b. Красная кривая соответствует поляризации (b) на рис. 8. Для α = 0⁰, т.е. света, падающего перпендикулярно поверхности, отношение E/E₀ равно 0,2. Тогда нет никакой разницы между случаем (a) и случаем (b). По мере увеличения угла α величина E/E₀ первоначально вообще не увеличивается, а наоборот уменьшается. Свет отражается все меньше и меньше. Величина E/E₀ достигает нуля для определенного угла. Этот угол α_B называется углом Брюстера. Он зависит от показателя преломления вещества. Для n = 1,5 он равен α_B = 56,3°. Для углов, превышающих α_B, отношение E/E₀ увеличивается и приближается к единице при значениях угла α, приближающихся к 90°. Тогда весь свет ведет себя как в случае (a).

Угол Брюстера удовлетворяет простому соотношению tg α_B = n .

Полная поляризация света при отражении

Рассмотрим далее, что произойдет, если неполяризованный свет, например, от обычной лампочки, будет падать на стекло под углом Брюстера. Такая волна может быть разложена на две поляризованные волны с перпендикулярными направлениями электрического поля, одна типа (a) и другая типа (b).

Каждая волна может быть разложена на две поляризованные волны с произвольно выбранными перпендикулярными направлениями электрического поля. Это вытекает из простого факта: каждый вектор на плоскости может быть представлен как сумма двух векторов, перпендикулярных друг другу (рис. 10). Это справедливо как для поляризованной, так и для неполяризованной волны.

Рис. 10. Разложение вектора электрического поля на два перпендикулярных направления

В случае неполяризованной волны, когда мы разложим ее на составляющие, окажется, что волна (a) будет частично отражена (синяя кривая на рис. 9.), а волна (b) не будет отражена вообще, но полностью проникнет в стекло (красная кривая на рис. 9.). Таким образом, отраженный свет будет содержать только один компонент, т.е. он будет полностью поляризован, с направлением электрического поля, как на рис. 2a.

Частичная поляризация света при отражении

Для всех углов α, отличных от α_B, в отраженном свете присутствуют обе составляющие: (a) и (b). За исключением α = 0⁰ и α до 90°, компонент (a) в среднем имеет большее значение, чем компонент (b). При вращении поляризатора наблюдаемая интенсивность света изменяется. Для некоторых углов это самый высокий угол, а для других — самый низкий. Однако полного исчезновения интенсивности света не наблюдается. График интенсивности света в зависимости от угла, на который был повернут поляризатор, показан на рис. 11.

Рис. 11. График интенсивности света в зависимости от угла, под которым установлен поляризатор, для углов падения, отличных от угла Брюстера

Мы называем такой свет частично поляризованным.

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Типы поляризации

Поляризация подразделяется на различные типы в зависимости от того, как ведут себя направление колебаний электрического поля и его величина.

• Линейная поляризация: направление колебаний электрического поля постоянно, но его величина периодически меняется.
• Круговая поляризация: здесь величина электрического поля постоянна, но направление его колебаний меняется с фиксированной угловой скоростью.
• Эллиптическая поляризация: при этом типе поляризации изменяется как величина электрического поля, так и направление его колебаний.

Название типов поляризации происходит из того факта, что при взгляде спереди вектор электрического поля имеет следующие геометрические формы (см. рисунок 12).

Рис. 12. Типы поляризации света

При линейной поляризации, например, вектор электрического поля движется вдоль линии, тогда как при круговой поляризации он движется вдоль окружности.

Видео:Разложение вектора по базису. 9 класс.Скачать

Примеры использования поляризации света

Наконец, мы приводим краткий список областей, в которых поляризация света имеет решающее значение. К ним относятся

• жидкокристаллические дисплеи (также называемые ЖК-дисплеи),
• солнцезащитные очки,
• 3D фильмы,
• анализ механических напряжений в прозрачных пластмассах,
• в фотографии.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Плоскость колебаний электрического вектора

В начале XIX века, когда Т. Юнг и О. Френель развивали волновую теорию света, природа световых волн была неизвестна. На первом этапе предполагалось, что свет представляет собой продольные волны, распространяющиеся в некоторой гипотетической среде – эфире . При изучении явлений интерференции и дифракции вопрос о том, являются ли световые волны продольными или поперечными, имел второстепенное значение. В то время казалось невероятным, что это поперечные волны, так как по аналогии с механическими волнами пришлось бы предполагать, что эфир – это твердое тело (поперечные механические волны не могут распространяться в газообразной или жидкой среде).

Однако, постепенно накапливались экспериментальные факты, свидетельствующие в пользу поперечности световых волн. Еще в конце XVII века было обнаружено, что кристалл исландского шпата (CaCO₃) раздваивает проходящие через него лучи. Это явление получило название двойного лучепреломления (рис. 3.11.1).

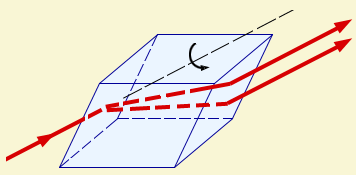Рисунок 3.11.1. В 1809 году французский инженер Э. Малюс открыл закон, названный его именем. В опытах Малюса свет последовательно пропускался через две одинаковые пластинки из турмалина (прозрачное кристаллическое вещество зеленоватой окраски). Пластинки можно было поворачивать друг относительно друга на угол (рис. 3.11.2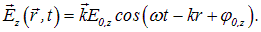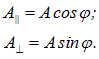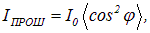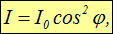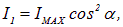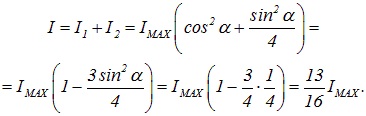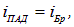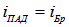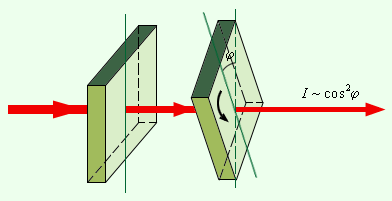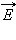). Рисунок 3.11.2. Интенсивность прошедшего света оказалась прямо пропорциональной : . Ни двойное лучепреломление, ни закон Малюса не могут найти объяснение в рамках теории продольных волн. Для продольных волн направление распространения луча является осью симметрии. В продольной волне все направления в плоскости, перпендикулярной лучу, равноправны. В поперечной волне (например, в волне, бегущей по резиновому жгуту) направление колебаний и перпендикулярное ему направление не равноправны (рис. 3.11.3). Рисунок 3.11.3. Таким образом, асимметрия относительно направления распространения (луча) является решающим признаком, который отличает поперечную волну от продольной. Впервые догадку о поперечности световых волн высказал в 1816 г. Т. Юнг. Френель, независимо от Юнга, также выдвинул концепцию поперечности световых волн, обосновал ее многочисленными экспериментами и создал теорию двойного лучепреломления света в кристаллах. В середине 60-х годов XIX века на основании совпадения известного значения скорости света со скоростью распространения электромагнитных волн Максвелл сделал вывод о том, что свет – это электромагнитные волны. К тому времени поперечность световых волн уже была доказано экспериментально. Поэтому Максвелл справедливо полагал, что поперечность электромагнитных волн является еще одним важнейшим доказательством электромагнитной природы света. Электромагнитная теория света приобрела должную стройность, поскольку исчезла необходимость введения особой среды распространения волн – эфира, который приходилось рассматривать как твердое тело. 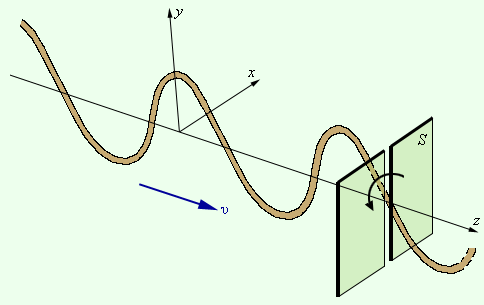В электромагнитной волне вектора и 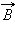перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны (рис. 2.6.3). Во всех процессах взаимодействия света с веществом основную роль играет электрический вектор 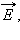поэтому его называют световым вектором . Если при распространении электромагнитной волны световой вектор сохраняет свою ориентацию, такую волну называют линейно поляризованной или плоско поляризованной (термин поляризация волн был введен Малюсом применительно к поперечным механическим волнам). Плоскость, в которой колеблется световой вектор 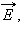называется плоскостью колебаний (плоскость на рис. 2.6.3), а плоскость, в которой совершает колебание магнитный вектор 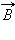– плоскостью поляризации (плоскость на рис. 2.6.3).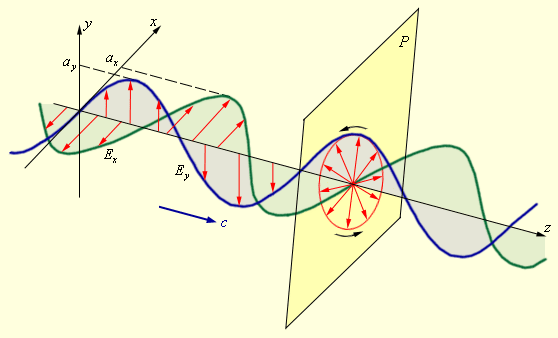 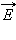Если вдоль одного и того же направления распространяются две монохроматические волны, поляризованные в двух взаимно перпендикулярных плоскостях, то в результате их сложения в общем случае возникает эллиптически поляризованная волна (рис. 3.11.4). Рисунок 3.11.4. В эллиптически поляризованной волне в любой плоскости , перпендикулярной направлению распространения волны, конец результирующего вектора за один период светового колебания обегает эллипс, который называется эллипсом поляризации . Форма и размер эллипса поляризации определяются амплитудами и линейно поляризованных волн и фазовым сдвигом между ними. Частным случаем эллиптически поляризованной волны является волна с круговой поляризацией (, ).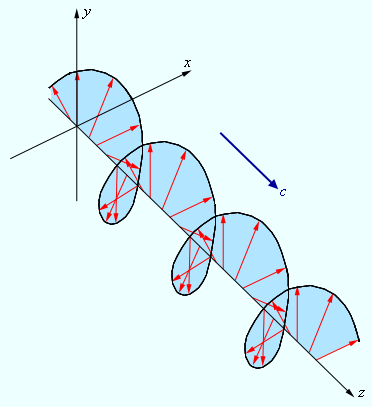 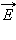Рис. 3.11.5 дает представление о пространственной структуре эллиптически поляризованной волны. Рисунок 3.11.5. Линейно поляризованный свет испускается лазерными источниками. Свет может оказаться поляризованным при отражении или рассеянии. В частности, голубой свет от неба частично или полностью поляризован. Однако, свет, испускаемый обычными источниками (например, солнечный свет, излучение ламп накаливания и т. п.), неполяризован . Свет таких источников в каждый момент состоит из вкладов огромного числа независимо излучающих атомов (см. § 3.2) с различной ориентацией светового вектора в излучаемых этими атомами волнах. Поэтому в результирующей волне вектор беспорядочно изменяет свою ориентацию во времени, так что в среднем все направления колебаний оказываются равноправными. Неполяризованный свет называют также естественным светом . 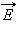В каждый момент времени вектор может быть спроектирован на две взаимно перпендикулярные оси (рис. 3.11.6).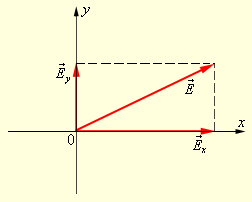 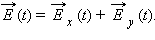Рисунок 3.11.6. Это означает, что любую волну (поляризованную и неполяризованную) можно представить как суперпозицию двух линейно поляризованных во взаимно перпендикулярных направлениях волн: Но в поляризованной волне обе составляющие и когерентны, а в неполяризованной – некогерентны, т. е. в первом случае разность фаз между и постоянна, а во втором она является случайной функцией времени. 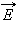Явление двойного лучепреломления света объясняется тем, что во многих кристаллических веществах показатели преломления волн, линейно поляризованных во взаимно перпендикулярных направлениях, различны. Поэтому кристалл раздваивает проходящие через него лучи (рис. 3.11.1). Два луча на выходе кристалла линейно поляризованы во взаимно перпендикулярных направлениях. Кристаллы, в которых происходит двойное лучепреломление, называются анизотропными . С помощью разложения вектора на составляющие по осям можно объяснить закон Малюса (рис. 3.11.2).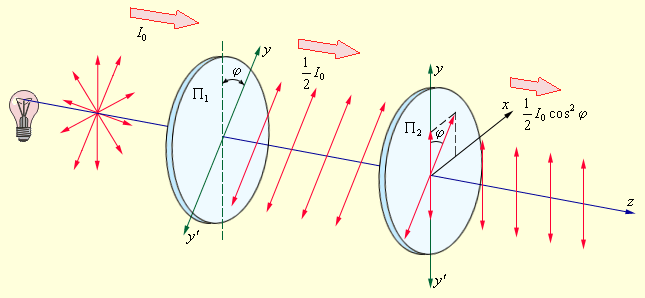 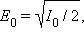У многих кристаллов поглощение света сильно зависит от направления электрического вектора в световой волне. Это явление называют дихроизмом . Этим свойством, в частности, обладают пластины турмалина, использованные в опытах Малюса. При определенной толщине пластинка турмалина почти полностью поглощает одну из взаимно перпендикулярно поляризованных волн (например, ) и частично пропускает вторую волну (). Направление колебаний электрического вектора в прошедшей волне называется разрешенным направлением пластинки. Пластинка турмалина может быть использована как для получения поляризованного света ( поляризатор ), так и для анализа характера поляризации света ( анализатор ). В настоящее время широко применяются искусственные дихроичные пленки, которые называются поляроидами . Поляроиды почти полностью пропускают волну разрешенной поляризации и не пропускают волну, поляризованную в перпендикулярном направлении. Таким образом, поляроиды можно считать идеальными поляризационными фильтрами . Рассмотрим прохождение естественного света последовательно через два идеальных поляроида и (рис. 3.11.7), разрешенные направления которых повернуты друг относительно друга на некоторый угол . Первый поляроид играет роль поляризатора. Он превращает естественный свет в линейно поляризованный. Второй поляроид служит для анализа падающего на него света. Рисунок 3.11.7. Если обозначить амплитуду линейно поляризованной волны после прохождения света через первый поляроид через то волна, пропущенная вторым поляроидом, будет иметь амплитуду . Следовательно, интенсивность линейно поляризованной волны на выходе второго поляроида будет равна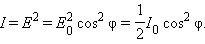 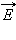Таким образом, в электромагнитной теории света закон Малюса находит естественное объяснение на основе разложения вектора на составляющие. 💡 Видео Вектор Умова-Пойнтинга ● 1Скачать Сложение волн, поляризованных в перпендикулярных плоскостяхСкачать Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать Поляризация плоской электромагнитной волныСкачать Поляризация света. Вращение плоскости поляризацииСкачать Урок 337. Сложение колебаний одной частоты. Метод векторных диаграммСкачать Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать 80. Поляризация ЭМВСкачать 1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать ТОЭ 26. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.Скачать Поделиться или сохранить к себе: Смотрите также Ящик с инструментами в векторе Якорь в векторе черно белый Який вектор колінеарний до будь якого вектора Як знайти точку в векторе Являются ли точки вершинами трапеции векторы Юрий бурлан тест на вектор Эффективность относится к вектору аудита исполнительному стратегическому Эмблема службы горючего вс рф в векторе