Вектор суммарного электрического поля (6 видео)

Вектор суммарного электрического поля

Задание 13. Два неподвижных точечных электрических заряда -q и +q (q> 0) расположены, как показано на рисунке. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор напряжённости суммарного электрического поля этих зарядов в точке А? Ответ запишите словом (словами).

Известно, что вектор напряженности электрического поля исходит из положительного заряда и входит в отрицательный заряд. Поэтому, в точке A мы увидим примерно следующую картину направления векторов напряженности электрического поля (см. синие стрелки на рисунке ниже).

Из рисунка видно, что вектор напряженности направлен вправо к отрицательному заряду.

Содержание

Вектор напряженности электрического поля
Характеристика электрического поля
Силовые линии
Что называется напряженностью электрического поля
Вектор суммарного электрического поля
🔥 Видео

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор напряженности электрического поля

По теории близкодействия взаимодействия между заряженными телами, удаленными друг от друга, происходит с помощью электромагнитных полей, создаваемых этими телами в окружающем их пространстве. Если поле было создано неподвижными частицами, то его относят к электростатическому. Когда происходят изменения во времени, получает название стационарного. Электростатическое поле является стационарным. Оно считается частным случаем электромагнитного поля.

Видео:НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Характеристика электрического поля

Силовая характеристика электрического поля – вектор напряженности, который можно найти по формуле:

E → = F → q , где F → — сила, действующая со стороны поля на неподвижный (пробный) заряд q . Его значение должно быть настолько мало, чтобы отсутствовала возможность искажать поле, напряженность которого с его помощью и измеряют. По уравнению видно, что напряженность совпадает по направлению с силой, с которой поле действует на единичный положительный пробный заряд.

У напряженности электростатического поля нет зависимости от времени. Когда она во всех точках поля одинакова, тогда поле называют однородным. В другом случае – неоднородным.

Видео:Урок 218. Напряженность электрического поляСкачать

Силовые линии

Чтобы изобразить электростатические поля графически, необходимо задействовать понятие силовых линий.

Силовые линии – это линии, касательные к которым в каждой точке поля совпадают с направлениями векторов напряженности в этих точках.

Такие линии в электростатическом поле разомкнутые. Они начинаются на положительных зарядах и заканчивают на отрицательных. Реже уходят в бесконечность или возвращаются из нее. Силовые линии поля не могу пересекаться.

Вектор напряженности электрического поля подчиняется принципу суперпозиции, а именно:

E → = ∑ i = 1 n E → i .

Результирующий вектор напряженности сводится к нахождению векторной суммы напряженностей, составляющих его «отдельные» поля. При распределении непрерывного заряда, поиск суммарной напряженности поля производится по формуле:

Интегрирование E → = ∫ d E → проводится по области распределения зарядов. Если их распределение идет по линии ( τ = d q d l — линейная плотность распределения заряда), то интегрирование E → = ∫ d E → тоже. Когда распределение зарядов идет по поверхности и поверхностная плоскость обозначается как σ = d q d S , тогда интегрируют по поверхности.

Интегрирование по объему выполняется, если имеется объемное распределение заряда:

ρ = d q d V , где ρ — объемная плотность распределения заряда.

Видео:42. Теорема Гаусса. Расчет электростатических полейСкачать

Что называется напряженностью электрического поля

Напряженность поля в диэлектрике равняется векторной сумме напряженностей полей, которые создают свободные E 0 → и связанные E p → заряды:

Зачастую бывают случаи, когда диэлектрик изотропный. Тогда запись напряженности поля имеет вид:

E → = E 0 → ε , где ε обозначает относительную диэлектрическую проницаемость среды в рассматриваемой точке поля.

Отсюда следует, что по выражению E → = E 0 → ε имеется однородный изотропный диэлектрик с напряженностью электрического поля в ε меньше, чем в вакууме.

Напряженность электростатического поля системы точечных зарядов равняется:

E → = 1 4 π ε 0 ∑ i = 1 n q i ε r i 3 r i → .

В системе СГС напряженность поля точечного заряда в вакууме:

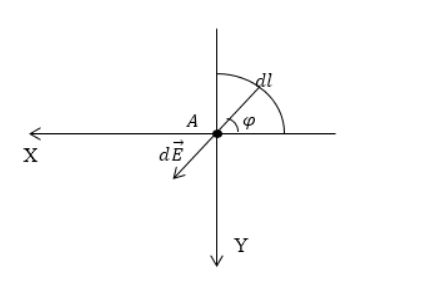
Дан равномерно распределенный заряд по четверти окружности радиуса R с линейной плотностью τ . Необходимо найти напряженность поля в точке А , являющейся центром окружности.

Решение

Произведем выделение на заряженной части окружности элементарного участка d l , который будет создавать элемент поля в точке А . Следует записать выражение для напряженности, то есть для d E → . Тогда формула примет вид:

d E → = d q R 3 R → R .

Проекция вектора d E → на ось О х составит:

d E x = d E cos φ = d q cos φ R 2 .

Произведем выражение d q через линейную плотность заряда τ :

d q = τ d l = τ · 2 πRdR .

Необходимо использовать d q = τ d l = τ · 2 πRdR для преобразования d E x = d E cos φ = d q cos φ R 2 :

d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,

где 2 π d R = d φ .

Далее перейдем к нахождению полной проекции E x при помощи интегрирования d E x = 2 π R τ d R cos φ R 2 = 2 π τ d R cos φ R = τ cos φ d φ R ,

по d φ с изменением угла 0 ≤ φ ≤ 2 π .

E x = ∫ 0 2 π τ cos φ d φ R = τ R ∫ 0 2 π cos φ d φ = τ R sin φ 0 2 π = τ R .

Перейдем к проекции вектора напряженности на О у :

d E y = d E sin φ = τ R sin φ d φ .

Следует проинтегрировать с изменяющимся углом π 2 ≤ φ ≤ 0 :

E y ∫ π 2 0 τ R sin φ d φ = τ R ∫ π 2 0 sin φ d φ = — τ R cos φ π 2 0 = — τ R .

Произведем нахождение модуля вектора напряженности в точке А , применив теорему Пифагора:

E = E x 2 + E y 2 = τ R 2 + — τ R 2 = τ R 2 .

Ответ: E = τ R 2 .

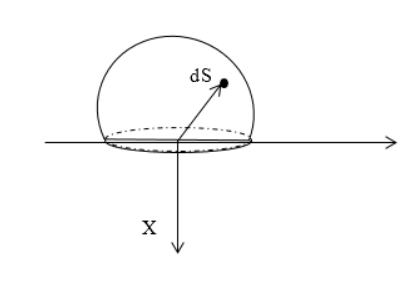
Найти напряженность электростатического поля равномерно заряженной полусферы с радиусом R . Поверхностная плотность заряда равняется σ .

Решение

Следует выделить на поверхности заряженной сферы элементарный заряд d q , располагаемый на элементе площади d S . Запись, используя сферические координаты d S , равняется:

d S = R 2 sin θ d θ d φ ,

при 0 ≤ φ ≤ 2 π , 0 ≤ θ ≤ π 2 .

Элементарная напряженность поля точечного заряда в системе С И :

d E → = d q 4 π ε 0 R 3 R → R .

Необходимо спроецировать вектор напряженности на О х :

d E x = d q cos θ 4 π ε 0 R 2 .

Произведем выражение заряда через поверхностную плотность заряда:

Подставим d q = σ d S в d E x = d q cos θ 4 π ε 0 R 2 , используя d S = R 2 sin θ d θ d φ , проинтегрируем и запишем:

E x = σ R 2 4 π ε 0 R 2 ∫ 0 2 π d φ ∫ 0 π 2 cos θ sin θ d θ = σ 4 π ε 0 2 π · 1 2 = σ 4 ε 0 .

Отсюда следует, что E = E x .

Ответ: напряженность полусферы в центре равняется E = σ 4 ε 0 .

Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Вектор суммарного электрического поля

На рисунке представлено расположение двух неподвижных точечных электрических зарядов и

Направлению вектора напряженности электрического поля этих зарядов в точке A соответствует стрелка

По принципу суперпозиции, напряженность поля в точке A есть сумма напряженностей полей, создаваемых зарядами и по отдельности. Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом, — от заряда. Таким образом, напряженности полей зарядов направлены в точке A в разные стороны. Поле точечного заряда ослабевает с расстоянием как заряды по величине одинаковые, поэтому поле от отрицательного заряда в точке A сильнее, чем поле от положительного заряда. Следовательно, направлению напряженности электрического поля в точке A соответствует стрелка 2.

Если мы помещаем отрицательный заряд в точку А, то не будут ли они отталкиваться с ближайшим (-q). Не понимаю, почему ответ не 4

Отрицательный заряд будет, конечно, будет отталкиваться. Но за направление вектора напряженности выбирается направление силы, действующей со стороны электрического поля на положительный заряд.

На рисунке показано расположение двух неподвижных точечных электрических зарядов и В какой из трех точек — А, B или C — модуль вектора напряженности суммарного электрического поля этих зарядов максимален?

4) во всех трех точках модуль напряженности поля имеет одинаковые значени

Поле отрицательного точечного заряда направлено к заряду, а поле, создаваемое положительным зарядом, — от заряда. Следовательно, в точках A и C поля направлены в разные стороны, а в точке B сонаправлены. Поле точечного заряда по модулю пропорционально величине заряда и обратно пропорционально квадрату расстояния до него: Таким образом, модуль вектора напряженности суммарного электрического поля этих зарядов максимален в точке B.

Т. е. точки A, B, C — пробные заряды?

Пробные (малые заряды) нужны для экспериментального исследования «сложных» электрических полей, создаваемых нетривиальными (неточечными) распределениями заряда.

Если изучается поле, создаваемое конечным числом точечных зарядов, нужды в пробных зарядах нет. Величину поля в каждой точке пространства можно определить, используя принцип суперпозиции, ведь поле, создаваемое точечным источником хорошо известно.

Так что говорить о размещении пробных зарядов в точках , и нет необходимости, ведь у Вас все равно нет, скажем, динамометра, чтобы определять силы, жействующие на пробные заряды, а есть только картинка 🙂

не понятно, почему в точках А и С поля будут направлены в разные стороны, у меня получается, что как раз в одну сторону.

В точке А поля от обоих зарядов направлены в разные стороны, поэтому они друг друга частично сокращают. Аналогично для точки С.

Напряженность электрического поля измеряют с помощью пробного заряда Если величину пробного заряда уменьшить в n раз, то модуль напряженности измеряемого поля

2) увеличится в n раз

3) уменьшится в n раз

4) увеличится в раз

Сила, с которой электрическое поле действует на пробный электрический заряд пропорциональна величине этого заряда, поэтому величина напряженности электрического поля не зависит от величины пробного заряда

по этой формуле же увеличится в n раз

Читайте внимательнее. Сила, действующая на пробный заряд, пропорциональна его величине. Если бы напряженность зависела от величины заряда, то какой бы был прок в такой характеристике поля?

Для электрической напряженности также существует формула E=k*q/r^2. по ней напряженность и заряд прямопропорциональны. как быть?

Напряженность создает другой заряд, который не изменяется.

Металлическому полому телу, сечение которого представлено на рисунке, сообщен отрицательный заряд. Каково соотношение между потенциалами точек 1, 2 и 3, если тело помещено в однородное электростатическое поле?

Металл является проводником. Проводник, помещенный в электростатическое поле является эквипотенциальным телом, то есть все его точки находятся под одинаковым потенциалом. Действительно, если предположить обратное и допустить, что в проводнике есть точки с разными потенциалами, то между этими точками будет ненулевая разность потенциалов, а значит, эти точки проводника будут находиться под ненулевым электрическим напряжением, но тогда в проводнике должен течь ток, что противоречит исходному предположению о том, что все электростатично. Таким образом, при помещении проводника в электростатическое поле заряды на его поверхности всегда перераспределяются таким образом, чтобы потенциал всех точек был одинаковым. Более того, если в проводнике имеется полость, то все точки полости также имеют потенциал, совпадающий по величине с потенциалом проводника. Это явление называется экранировкой электростатического поля. Таким образом, верно утверждение 1.