Вектор строку в вектор столбец matlab (2 видео)

Вектор строку в вектор столбец matlab

Выше были рассмотрены операции с простыми переменными. Однако с их помощью сложно описывать сложные данные, такие как случайный сигнал, поступающий на вход фильтра или хранить кадр изображения и т.п. Поэтому в языках высокого уровня предусмотрена возможность хранить значения в виде массивов. В MatLab эту роль выполняют векторы и матрицы.

Ниже показан пример задания вектора с именем a, и содержащий значения 1, 2, 3, 4:

a = [1 2 3 4]; % вектор-строка

Для доступа к тому или иному элементу вектора используется следующая конструкция языка:

disp( a(1) ); % отображение значения 1-го элемента вектора
disp( a(2) ); % отображение значения 2-го элемента вектора
disp( a(3) ); % отображение значения 3-го элемента вектора
disp( a(4) ); % отображение значения 4-го элемента вектора

т.е. нужно указать имя вектора и в круглых скобках написать номер индекса элемента, с которым предполагается работать. Например, для изменения значения 2-го элемента массива на 10 достаточно записать

a(2) = 10; % изменение значения 2-го элемента на 10

Часто возникает необходимость определения общего числа элементов в векторе, т.е. определения его размера. Это можно сделать, воспользовавшись функцией length() следующим образом:

N = length(a); % (N=4) число элементов массива а

Если требуется задать вектор-столбец, то это можно сделать так

a = [1; 2; 3; 4]; % вектор-столбец

b = [1 2 3 4]’; % вектор-столбец

при этом доступ к элементам векторов осуществляется также как и для векторов-строк.

Следует отметить, что векторы можно составлять не только из отдельных чисел или переменных, но и из векторов. Например, следующий фрагмент программы показывает, как можно создавать один вектор на основе другого:

a = [1 2 3 4]; % начальный вектор a = [1 2 3 4]
b = [a 5 6]; % второй вектор b = [1 2 3 4 5 6]

Здесь вектор b состоит из шести элементов и создан на основе вектора а. Используя этот прием, можно осуществлять увеличение размера векторов в процессе работы программы:

a = [a 5]; % увеличение вектора а на один элемент

Недостатком описанного способа задания (инициализации) векторов является сложность определения векторов больших размеров, состоящих, например, из 100 или 1000 элементов. Чтобы решить данную задачу, в MatLab существуют функции инициализации векторов нулями, единицами или случайными значениями:

a1 = zeros(1, 100); % вектор-строка, 100 элементов с
% нулевыми значениями
a2 = zeros(100, 1); % вектор-столбец, 100 элементов с
% нулевыми значениями
a3 = ones(1, 1000); % вектор-строка, 1000 элементов с
% единичными значениями
a4 = ones(1000, 1); % вектор-столбец, 1000 элементов с
% единичными значениями
a5 = rand(1000, 1); % вектор-столбец, 1000 элементов со
% случайными значениями

Матрицы в MatLab задаются аналогично векторам с той лишь разницей, что указываются обе размерности. Приведем пример инициализации единичной матрицы размером 3х3:

E = [1 0 0; 0 1 0; 0 01]; % единичная матрица 3х3

E = [1 0 0
0 1 0
0 0 1]; % единичная матрица 3х3

Аналогичным образом можно задавать любые другие матрицы, а также использовать приведенные выше функции zeros(), ones() и rand(), например:

A1 = zeros(10,10); % нулевая матрица 10х10 элементов

A2 = zeros(10); % нулевая матрица 10х10 элементов
A3 = ones(5); % матрица 5х5, состоящая из единиц
A4 = rand(100); % матрица 100х100, из случайных чисел

Для доступа к элементам матрицы применяется такой же синтаксис как и для векторов, но с указанием строки и столбца где находится требуемый элемент:

A = [1 2 3;4 5 6;7 8 9]; % матрица 3х3
disp( A(2,1) ); % вывод на экран элемента, стоящего во
% второй строке первого столбца, т.е. 4
disp( A(1,2) ); % вывод на экран элемента, стоящего в
% первой строке второго столбца, т.е. 2

Также возможны операции выделения указанной части матрицы, например:

B1 = A(:,1); % B1 = [1; 4; 7] – выделение первого столбца
B2 = A(2,:); % B2 = [1 2 3] – выделение первой строки
B3 = A(1:2,2:3); % B3 = [2 3; 5 6] – выделение первых двух
% строк и 2-го и 3-го столбцов матрицы А.

Размерность любой матрицы или вектора в MatLab можно определить с помощью функции size(), которая возвращает число строк и столбцов переменной, указанной в качестве аргумента:

a = 5; % переменная а
A = [1 2 3]; % вектор-строка
B = [1 2 3; 4 5 6]; % матрица 2х3
size(a) % 1х1
size(A) % 1х3
size(B) % 2х3

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Содержание

MATLAB — Векторы
Строки Векторы
Векторы столбцов
Ссылка на элементы вектора
Общие принципы работы системы Matlab
📹 Видео

Видео:Работа с массивами. Вектор столбцы и вектор строки 2. Урок 8Скачать

MATLAB — Векторы

Вектор — это одномерный массив чисел. MATLAB позволяет создавать два типа векторов —

Векторы строк
Векторы столбцов

Видео:Основы МАТЛАБ.РАБОТА С МАССИВАМИ. ВЕКТОРЫ-СТОЛБЦЫ И ВЕКТОРЫ-СТРОКИСкачать

Строки Векторы

Векторы строк создаются путем заключения набора элементов в квадратных скобках с использованием пробела или запятой для разделения элементов.

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

Векторы столбцов

Векторы столбцов создаются заключением набора элементов в квадратные скобки с использованием точки с запятой для разделения элементов.

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Видео:Matlab создание вектора данныхСкачать

Ссылка на элементы вектора

Вы можете ссылаться на один или несколько элементов вектора несколькими способами. I- й компонент вектора v обозначается как v (i). Например —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Когда вы ссылаетесь на вектор с двоеточием, например, v (:), в нем отображаются все компоненты вектора.

Видео:Работа со строками в MATLABСкачать

Общие принципы работы системы Matlab

Лабораторная работа №1

По дисциплине:Цифровая обработка сигналов

Тема:Общие принципы работы системы MatLab

Выполнили: ст. гр. И-33 БН

Проверил: ст. преподаватель

Лабораторная работа 1

Общие принципы работы системы Matlab

1.1 Ознакомление с системой MatLab, правилами создания числовых массивов и приобретение практических навыков по использованию средств системы для работы с ними

2 Основное оборудование:

2.1. Персональный компьютер.

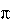
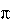
3.1 Создать вектор-строку: начальный элемент равен – , конечный , шаг равен 0.1. Транспонировать строку в столбец.

3.2 Создать три вектор-строки из 5 элементов fi= [xn, xn-1, xn-2, xn-3, xn-4], где n = 5 для х = 2, 3, 4. Объединить эти строки в матрицу А(3 × 5).

f2=[15 14 13 12 11]

f3=[20 19 18 17 16]

3.3 Создать три вектор-столбца из 5 элементов арифметической прогрессии. Элемент арифметической прогрессии рассчитывается по формуле:

где аn–1 – предыдущий элемент; аn– последующий.

Пять элементов вектора формируются, начиная с задания первого элемента а и c использованием шага арифметической прогрессии d для задания последующих элементов:

Для первого вектор-столбца a = 2; d = 1;

Для второго вектор-столбца a = 7; d = 2;

Для третьего вектор-столбца a = 10; d = –2.

3.3.1 Объединить эти вектор-столбцы в матрицу В(5 × 3).

3.3.2 Транспонировать матрицу В из предыдущего пункта задания и объединить с матрицей А в матрицу М(6 × 5).

3.3.3 Из матрицы A убрать вторую строку.

3.3.4 У матрицы В обнулить третью строку и убрать две последние строки.

3.3.5 Создать матрицу Н(2 2) путем выделения первых двух

строк и столбцов матрицы М из четвертого пункта задания.

3.3.6 Создать с помощью функции repmat матрицу, состоящую из 2 × 3 матриц Н.

3.3.7 Создать матрицы размерностью 3 × 3: C – единиц; D – нулей; E – равномерно распределенных случайных чисел; F – нормально-распределенных случайных чисел.

3.3.8 Найти минимальный элемент в матрице равномерно-распределенных чисел размерностью 3 5, используя функцию reshape.

4.3.9 Создать символьные константы: а) Миру мир; б) Введите матрицу, ввести комментарий:

Использование интерактивного ввода.

5 Контрольные вопросы:

5.1Как представляется информация в системе MatLab?

Название системы MatLab происходит от слов Matrix Laboratory (матричная лаборатория). Пакет ориентирован на обработку массивов данных.

В интерфейс системы MatLab входят следующие панели:

Command Window (Окно Команд), где проводятся все расчеты и операции;

Launch Pad (Окно Разделов), где можно получить доступ к различным модулям ToolBox;

Workspace (Рабочее пространство), где отображается текущий набор переменных, введенных пользователем в командном окне;

Current Directory (Текущий каталог), где можно установить текущий

каталог;

Command History (История команд), где хранятся команды, набираемыепользователями.

5.2 Как можно создать векторы в системе MatLab?

Рассмотрим некоторые способы формирования числовых массивов. При их создании можно использовать:

Квадратные скобки; Специальную конструкцию j:i:k; Конкатенацию (объединение);

Специальные матричные функции.

Для создания вектор-строки используются квадратные скобки с перечислением элементов строки через пробел или запятую и специальная конструкция j:i:k с указанием начального значения вектора – j, шага – i и конечного значения вектора – k через двоеточие (если значение шага равно 1, его можно не указывать).

Для создания вектор-столбца элементы вектора перечисляются через точку с запятой в квадратных скобках или транспонируется полученный ранее вектор- строка. Для выполнения операции транспонирования используется одиночная кавычка (‘), которая ставится после индетификатора, определяющего транспонируемую структуру. Для комплексных матриц транспонирование дополняется сопряжением матрицы. Точка с одиночной кавычкой (.’) используется для транспонирования массива без операции сопряжения для комплексных матриц.

5.3 Какой вектор генерирует функция logspace?

Функцияlogspaceгенерирует вектор равноотстоящих в логарифмическом масштабе точек. Она особенно эффективна при создании вектора частот.

5.4 Как можно создать матрицы в системе MatLab?

Для создания матрицы можно использовать следующие способы ввода элементов в квадратных скобках:

1. По строкам, разделяющимся точкой с запятой;

2. По столбцам, заданным в квадратных скобках;

3. По строкам в интерактивном режиме.

5.6Каким образом производится индексация массивов в системе MatLab, удаление, обнуление строк, столбцов?

Элементы массивов обладают двумя свойствами: порядковым номером (индексом) в массиве и собственно значением. Нумерация элементов в системе MatLab начинается с единицы. Для указания индексов элементов массивов используются круглые скобки (ошибка при индексации массива генерируется в том случае, если индекс элемента меньше единицы или больше размера массива).

Если надо изменить значение всего столбца или строки, то номера, обозначающие диапазон значений, не указываются и остается одно двоеточие.

5.7 Чем отличается определение почленных и матричных операций в системе MatLab?

Почленные операции обращаются к определенному значению матрицы, а матричные операции наоборот обращаются ко всей матрице.

5.8 Как получить транспонированный массив?

транспонирование матрицы производится при помощи апострофа

5.9 Какие особенности существуют при транспонировании массива комплексных чисел?

Для создания вектор-столбца элементы вектора перечисляются через точку с запятой в квадратных скобках или транспонируется полученный ранее вектор-строка. Для выполнения операции транспонирования используется одиночная кавычка(‘), которая ставится после индетификатора, определяющего транспонируемую структуру . Для комплексных матриц транспонирование дополняется сопряжением матрицы. Точка с одиночной кавычкой(.’) используется для транспонирования массива без операции сопряжения для комплексных матриц.

5.10 Как можно объединить матрицы?

конкатенации —объединения малых матриц в большую

5.11 Как создаются строковые константы?

Для задания строковых констант в MATLAB используются апострофы

5.12 Какие системные переменные и константы есть в системе MatLab?

i или j — мнимая единица (корень квадратный из -1);

pi – число п — 3.1415926. ;

eps — погрешность операций над числами с плавающей точкой (2- 52 );

realmin — наименьшее число с плавающей точкой (2- 1022 );

realmax — наибольшее число с плавающей точкой (2 1023 );

inf — значение машинной бесконечности;

ans — переменная, хранящая результат последней операции и обычно вызывающая его отображение на экране дисплея;