Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №29. Радианная мера угла
Перечень вопросов, рассматриваемых в теме:
1) Понятие тригонометрической окружности;
2) Поворот точки вокруг начала координат;
3) Длина дуги окружности и площадь кругового сектора.
Глоссарий по теме
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Теоретический материал для самостоятельного изучения
На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.
На окружности можно выделить дугу. А если рассмотреть круг — часть плоскости, ограниченной окружностью — то можно выделить круговой сектор.
«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей
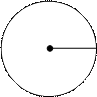
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)
Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии, 

Вычислите длину каждой дуги.
Ответ. длина каждой дуги равна 
Длина полуокружности равна 


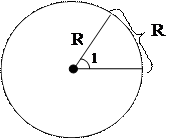
Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.

Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.


Длину дуги l окружности радиуса R (рис.4)
можно вычислять по формуле
А площадь S кругового сектора радиуса R и дугой 
находят по формуле: 

Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
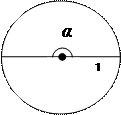
Введём понятие поворота точки. (рис.2)
- Пусть
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
- Пусть
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол 
угол 
Примеры и разбор решения заданий тренировочного модуля
Найти градусную меру угла, равного 
Решение: Используя формулу (1),
находим 
Так как 


Ответ: 
Пример 2. Найти радианную меру угла, равного 60
Вычисляем по формуле (2): 

При обозначении мер угла, наименование «рад» опускают.
Ответ: 

Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера 
Решение: Используя формулу (3),
получим:
Ответ: 
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла 
По формуле (4) вычисляем
Ответ: 45 
Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный 
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как 
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны 
На окружности можно найти координаты любой точки.
Ответ:
Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

лекция. Радианная мера угла. Тема Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа
| Название | Тема Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа |
| Анкор | лекция |
| Дата | 08.03.2021 |
| Размер | 439.37 Kb. |
| Формат файла |  |
| Имя файла | Радианная мера угла.docx |
| Тип | Документы #182619 |
| Подборка по базе: ИДЗ_5 тема_Сегментирование рынка_часть 2_экономика.docx, Логика_Практическое занятие. Тема 5.1.docx, 4 тема 3 доклад.docx, теория государства и права тема 1.docx, Философия Тема 1.2.docx, Экспликация тематического концерта.docx, МДК 01.01 Тема 1.1.2. Судовые электрические приводы.doc, инструкция о мерах ПБ в казарме 334 1 эт.docx, Годовой тематический план занятий с м.doc, тези тема 1.docx Тема: Радианная мера угла. Вращательное движение. Синус, косинус, тангенс и котангенс числа
Градусная мера.Здесь единицей измерения является градус (обозначение °) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. 1/60 часть градуса называется минутой (обозначают 1 ‘ ). 1/60 часть минуты называется секундой (обозначают 1 » ). Радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги. Градусная мера угла в 1 радиан равна: Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е. Если угол содержит α радиан, то его градусная мера равна Наиболее активные студенты участвуют при решении примеров на поиск радианной и градусной меры угла. Найти радианную меру угла равного 1) 30°, 2)135° 1) 30° = 30·π / 180 = π/6 2) 135° = 135·π/180 = 3π/4 Найти градусную меру угла выраженного в радианах 1) π/3 , 2) 4·π/5 2) 4π/5 = 4·180°/5 = 144° 1) 45° 4) 100° 7) 215° 2) 15° 5) 200° 8) 150° 3) 72° 6) 360° 9) 330° 2
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе. Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему. Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему. Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin, cos, tg и ctg соответственно. Давайте найдем значения синуса, косинуса, тангенса и котангенса углов 30°,45° и 60°. Запишем все значения углов в таблицу: Предлагаю вам алгоритм, благодаря которому вы легко, в течение минуты восстановите в памяти все вышеуказанные значения: 2. Напротив синуса пишем числа от нуля до четырёх (под значениями углов). Напротив косинуса от 4 до 0: 3. Далее извлекаем корень: Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и котангенса: вы сможете найти значения для указанных углов. Видео:Радианная мера угла. 9 класс.Скачать  Тема 4. Основы тригонометрииРадианная мера угла. Вращательное движение. Соотношение между градусной и радианной мерами угла. Начертим окружность радиуса равного единице (окружность произвольного радиуса, но по договоренности он будет равен единице). Длина окружности l=2πr Длина половины окружности l/2=π Угол α – развернутый (равен 180°). — Данный угол – центральный (так как его вершина совпадает с центром окружности), а это значит, что величина данного угла определяется длиной его дуги, т.е. получаем, что π=180°. — 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности. — 1 радиан – это постоянная величина, как и градус, и она не зависит от радиуса окружности, в которой построена. 1 радиан приближенно равен 57 градусов. — Радианная и градусная меры взаимосвязаны, угол, представленный в одной мере можно выразить в другой: π=180°, тогда 1°=π/180. — Если 1°=π/180, то можно выразить в радианной мере любой угол. 90°= Обратная задача: переведите величину угла из радианной меры в градусную. π=180° 2π=180°·2=360°; π/2=180°/2=90°; π/6=180°/6=30°; 3π/2=180°·3/2=270°. 🔍 ВидеоТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  10 класс, 11 урок, Числовая окружностьСкачать  Вращательное движение. 10 класс.Скачать  Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать  Угловая скорость и радианная мера углаСкачать  Тригонометрическая окружность. Как выучить?Скачать  ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать  Как искать точки на тригонометрической окружности.Скачать  🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать  Визуализация гравитацииСкачать  Урок 1. Радианная мера угла. Вращательное движение.Скачать  ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать  Физика - движение по окружностиСкачать  Поступательное и вращательное движения.Скачать  Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать  Зачем нужны синусы и косинусы?Скачать  Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать  |






 Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 
 точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол — α.













 ) 4) 6)
) 4) 6)








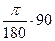 =
= 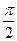 ; 60°=
; 60°= 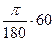 =
= 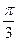 ; 45°=
; 45°= 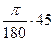 =
= 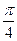 ; 30°=
; 30°= 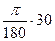 =
= 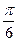 ; 270°=
; 270°= 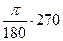 =
= 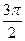 ; 360°=
; 360°= 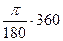 =2π.
=2π.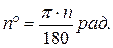 , где n – количество градусов.
, где n – количество градусов.