Вектор столбец в вектор строку scilab (7 видео)

IT Novella

Данный пост является продолжением поста Основы работы в Scilab.

Векторы и матрицы представляют собой одномерный и двумерный массивы.

Значение нижней границы индексации элементов массива в Scilab по умолчанию равно единице.

Одномерный массив (вектор-строку) можно задать с помощью команды

где X -название массива, a и b — значения первого и последнего элементов массива, h — шаг, с которым изменяются элементы массива. Возможна запись вида

В этом случае шаг автоматически принимается равным единице. Пример. Задать вектор-строку X с элементами -2,-1,0,1,2.

Пример. Задать вектор-строку X с элементами -2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2.

Другой способ определить вектор — перечислить все его элементы. В этом случае нужно выполнить команду

где X -имя вектора, x1,x2. xn — элементы массива. Пример. Задать вектор-строку X с элементами -5, 0.5, -7, 25.

Для того, чтобы задать вектор-столбец, необходимо перечислить элементы через точку с запятой. Пример. Задать вектор-столбец X с элементами -5, 0.5, -7, 25.

Другой способ задать вектор-столбец — использовать транспонирование матриц. Операция транспонирования задается с помощью знака ‘. Пример.

Для доступа к элементам вектора нужно указать название вектора и в круглых скобках номер элемента. Пример.

Для того, чтобы задать матрицу с элементами xij, нужно выполнить команду вида

Для доступа к элементам нужно указать название матрицы и в круглых скобках номер элемента. Пример.

Матрицы можно формировать на основе имеющихся

С помощью знака «:» можно выполнять различные операции с матрицами Пример.

При работе с матрицами в пакете Scilab можно использовать следующие операции: 1. + — сложение; Пример.

Если к заданной матрице применить некоторую функцию, то элементы матрицы будут преобразованы в соответствии с этой функцией. Пример.

При работе с матрицами можно использовать встроенные функции. Рассмотрим некоторые из них. Функция length(X) возвращает количество элементов матрицы X. Пример.

Функция size(X) возвращает вектор, содержащий количество строк и столбцов матрицы X. Пример.

Функция max(X) возвращает максимальный элемент матрицы X.

Функция min(X) возвращает минимальный элемент матрицы X.

Функция sum(X) возвращает сумму элементов матрицы X.

Функция prod(X) возвращает произведение элементов матрицы X.

Функция det(X) возвращает определитель матрицы X.

Функция inv(X) возвращает матрицу, обратную к X.

Содержание

Массивы в Scilab
2.1 Одномерные массивы (столбцы и строки)
2.2 Двумерные массивы (матрицы)
2.3 Специальные функции для векторов и матриц
Описание команд и функций Scilab
Скалярные величины. Векторы.
🔥 Видео

Видео:Работа с матрицами в ScilabСкачать

Массивы в Scilab

Scilab — матрично-ориентированный язык. Под массивами в данном мат. пакете понимаются конструкции, используемые в линейной алгебре: матрицы, векторы-строки и векторы-столбцы.

Под массивами в данном случае понимаются конструкции, используемые в линейной алгебре: матрицы, векторы-строки и векторы-столбцы.

Важно! Нумерация элементов массива в Scilab начинается с 1.

Видео:Работа с массивами. Вектор столбцы и вектор строки 1. Урок 7Скачать

2.1 Одномерные массивы (столбцы и строки)

Задать одномерный массив в Scilab можно следующим образом:

Здесь MAS – имя переменной, куда будет записан сформированный массив, v1 – значение первого элемента массива, vmax – значение последнего элемента массива, d – шаг, с которым будет происходить формирование элементов.

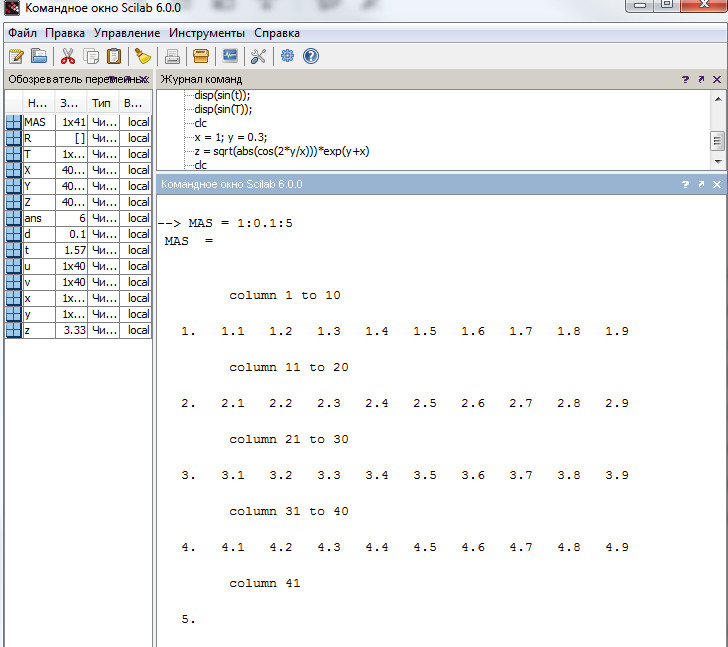
Например, сформируем массив с элементами от 1 до 5 с шагом 0.1 (листинг 4).

Листинг 4. Задание одномерного массива из 41 элемента.

Сформировать одномерный массив можно и непосредственным перечислением всех его элементов через запятую или пробел:

MAS = [v1, v2, … , vmax] или MAS = [v1 v2 … vmax]

Отметим, что данные способы формируют вектор-строку в которую записаны всего vmax элементов.

Для поэлементного задания вектор-столбца нужно разделять элементы массива точкой с запятой «;», то есть, воспользоваться записью:

Обращение к элементу массива происходит через указание номера элемента в круглых скобках у имени массива. Чтобы выбрать 2-й элемент одномерного массива MAS, необходимо ввести команду:

Создадим вектор-строку row из 11 элементов, начиная с 0 с шагом 0.1. Это делается следующим образом:

Сейчас row — это вектор-строка вида ( (0; 0.1; 0.2; 0.3; 0.4; 0.5; 0.6 ;0.7; 0.8 ;0.9; 1) )

Получим 5-й эелемент вектор-строки row и выведем этот элемент:

x=row(5); // присвоили переменной х значение, записанное в 5-й столбец строки row
disp(x); // выведет 0.4

Видео:Vectors in ScilabСкачать

2.2 Двумерные массивы (матрицы)

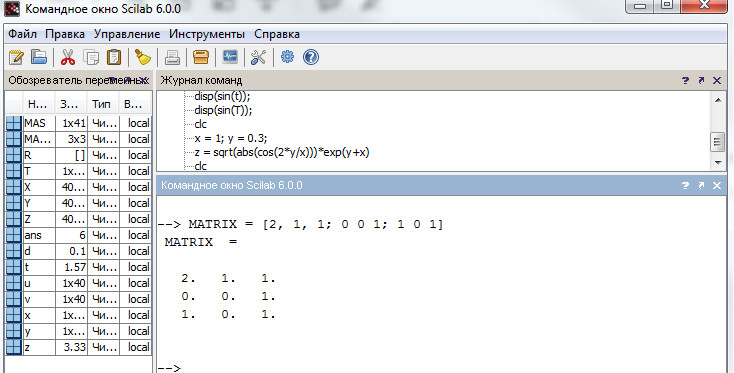
Двумерные массивы, или матрицы, также задаются при помощи квадратных скобок, при этом строки матрицы разделяются точкой с запятой «;», а столбцы — запятой или пробелом (листинг 5).

Листинг 5. Задание матрицы поэлементно.

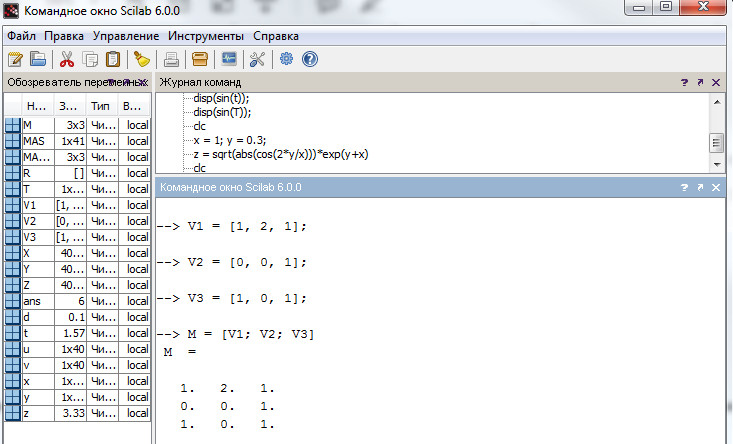
Кроме того, матрица может быть сформирована из векторов-строк или векторов-столбцов, заданных ранее (листинг 6).

Листинг 6. Задание матрицы из сформированных строк V1, V2, V3.

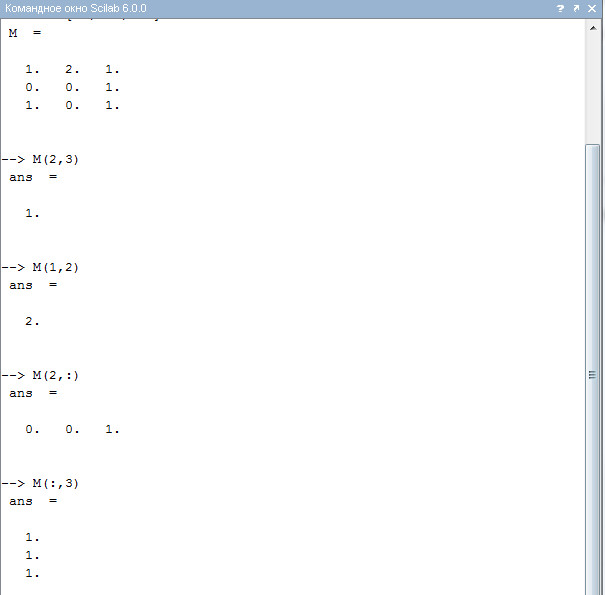
Обращение к элементу матрицы происходит через указание номера строки и столбца в круглых скобках у имени матрицы. Например, чтобы выбрать 3-й элемент из второй строки матрицы M, необходимо ввести команду:

M(2,3) // элемент из 2-й строки 3-го столбца 1

Отметим, что значения элементов матрицы можно использовать, присвоив их значения некоторым переменным, например:

Важную роль в работе с матрицами играет знак двоеточия «:». Указывая его, можно получить целую строку или целый столбец. Например, чтобы выбрать третий столбец матрицы, нужно записать M(:,3). А чтобы получить все элементы второй строки, нужно записать M(2,:). Смотри (листинг 7).

Листинг 7. Выбор элементов m23, m12 матрицы М; 2-й строки и 3-го столбца матрицы М.

Видео:Решение уравнений в ScilabСкачать

2.3 Специальные функции для векторов и матриц

В Scilab предусмотрены специальные функции для работы с матрицами. Эти функции обеспечивают быстрое создание распространенных типов матриц. Такими функциями являются следующие:

Кроме того, в мат. пакете есть ряд функций, полезных для решения задач линейной алгебры и устойчивости систем линейных дифференциальных уравнений.

det(M) – вычисление определителя квадратной матрицы;

spec(M) – находит собственные числа матрицы М;

Отметим, что для работы с матрицами и векторами предусмотрены стандартные операции сложения «+», матричного умножения и умножения на число «*», вычитания «-», возведения в степень «^», деления « / ».

Отдельно стоит выделить операции транспонирования «’» и поэлементного умножения « .* ».

Результаты операций с матрицами продемонстрированы ниже на Листинге 8.

Листинг 8. Операции матричного умножения, поэлементного умножения и транспонирования.

Видео:#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy урокиСкачать

Описание команд и функций Scilab

Видео:Решение систем линейных уравнений в Scilab.aviСкачать

Скалярные величины. Векторы.

Scilab является программой, оптимизированной для работы с массивами данных (матрицами). Скалярные величины и векторы можно рассматривать как частные случаи матриц.

В Scilab определены стандартные скалярные переменные, которые начинаются со знака %. Эти переменные защищены и не могут быть переопределены пользователем.

Перечислим эти переменные:

• мнимая единица —%i
• число Pi =3.1415927 — %pi
• число е = 2.7182818 — %е
• бесконечность — %inf
• булевское true — %t
• булевское false — %f

Scilab работает, как с действительными, так и с комплексными числами.

Пример 1. Записать комплексное число х = 1 + 2/.

Решение. Введем в командной строке выражение —>x=7+%i*2

На экране отобразится: х =

Вектор-строка задаётся следующим образом: в квадратных скобках через запятую задаются необходимые элементы вектора.

Пример 2. Задать числа 0, -3, л, 9 в виде вектора-строки.

Решение. Введем в командной строке выражение —>v=[0,-3,%pi,9]

На экране отобразится:

Для задания вектор-столбца его элементы должны быть разделены с помощью точки с запятой.

Пример 3. Задать вектор-столбец с числовыми элементами 40, 3/, 7, 7.

Решение. Зададим в командной строке вектор-столбец

На экране отобразится: v =

Также возможна операция транспонирования (преобразование вектор-столбец в вектор-строку и наоборот). Операция транспонирования задаётся следующим образом: с = Ь’

Пример 4. Транспонировать вектор-столбец в вектор-строку.

Решение. Зададим в командной строке вектор-столбец —>b=[ 1 ;2;3]

На экране отобразится: b =

Задать вектор — строку х с областью изменения х от л’„„„ до х_тах, с равномерным шагом delta можно следующим образом: х = [x_mj„:delta:x_max], где x_max, x_mj„ и delta могут быть арифметическими выражениями.

Пример 5. Задать вектор-строку с областью изменения от 0 до

Решение. Введем в командной строке выражение

На экране отобразится: х =

0. 1.5 3. 4.5 6. 7.5 9. 10.5.

Вектор-строку, элементы которой будут последовательными целыми числами от N до М можно создать, выполнив команду N:M.

Пример 6. Задать вектор-строку, содержащую целые числа от 2 до 5.

Решение. Введем в командной строке выражение —>а=(2:5)

На экране отобразится: а =

Если необходимо создать строку с элементами, которые будут отличаться на определённое число, то используют формат команды N:I:M.

Пример 7. Задать вектор-строку с числами от 2 до 6, отличающиеся на число 2.

Решение. Введем в командной строке выражение —>а=(2:2:6)

На экране отобразится: а =