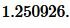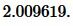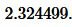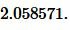- Ваш ответ
- решение вопроса
- Похожие вопросы
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- В треугольник вписана окружность радиуса 4 см?
- Точка касания окружности, вписанной в прямоуугольный треугольник, делит гипотенузу на отрезки, равные 8 и 12?
- В равнобедренный треугольник вписана окружность радиус которой равен 10 точка касания делит боковую сторону на отрезки длины которых относятся как 8 : 5 считая от вершины равнобедренного треугольника ?
- Окружность, вписанная в треугольник, делит точкой касания гипотенузу на отрезки 12 и 5?
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию?
- Ребят, помогите, пожалуйста?
- Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 4, считая от вершины, противолежащей основанию?
- В прямоугольном треугольнике точка касания вписанной в него окружности и гипотенузы делит гипотенузу на отрезки, длины которых равны 3 и 7, найдите площадь треугольника?
- В треугольник с периметром, равным 84, вписана окружность?
- В треугольник, стороны которого равны 6, 9, 11, вписана окружность?
- Одна из сторон треугольника равно 30 см, а другая сторона делится точкой касания вписанной окружности на отрезки длиной 12 см и 14 см, считая от конца неизвестной стороны?
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Ваш ответ
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

решение вопроса
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 606,989
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:ЕГЭ Математика Задание 6#27935Скачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
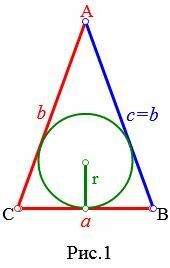
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
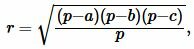 | (1) |
где полупериметр p вычисляется из формулы:
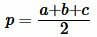 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac, ) | (3) |
| ( small p-a=frac-a ) ( small =frac, ) | (4) |
| ( small p-b=p-c=frac-b ) ( small =frac. ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
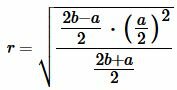 , , |
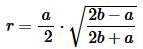 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
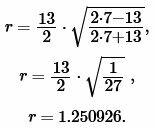 |
Ответ:
Видео:Геометрия В равнобедренный треугольник вписана окружность Точка касания делит боковую сторонуСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
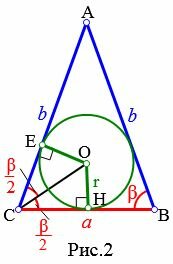 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac. ) Для прямоугольного треугольника OCH можно записать:
| ( small frac=frac<large frac>=mathrmfrac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrmfrac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
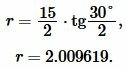 |
Ответ:
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
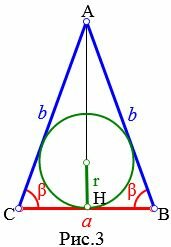 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac=frac<large frac>= cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrmfrac=frac cdot mathrmfrac ) ( small =b cos beta cdot mathrmfrac ) |
| ( small r=b cdot cos beta cdot mathrmfrac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
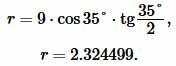 |
Ответ:
Видео:№691. Точка касания окружности, вписанной в равнобедренный треугольник, делит однуСкачать
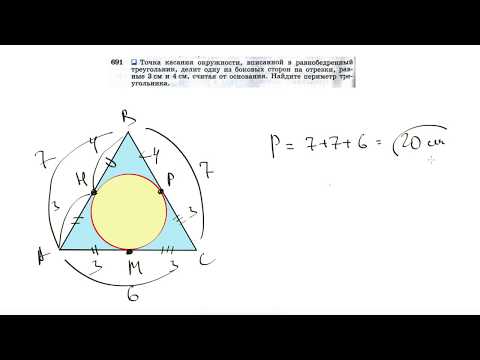
4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
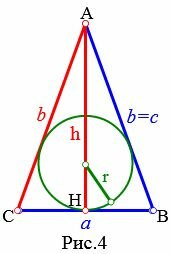 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
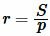 , , | (13) |
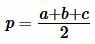 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( fracright)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac+b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac<large h cdot sqrt><large b+ sqrt> ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
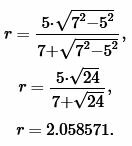 |
Ответ:
Видео:Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторонСкачать
5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
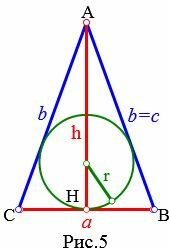
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac+h^2-h^2>><large frac cdot sqrt+ sqrt<frac+h^2-h^2>>) ( small = large frac< h cdot frac>< frac cdot sqrt+frac >) |
| ( small r=large frac<a+ sqrt>) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
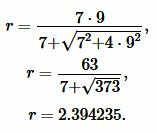 |
Ответ:
Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

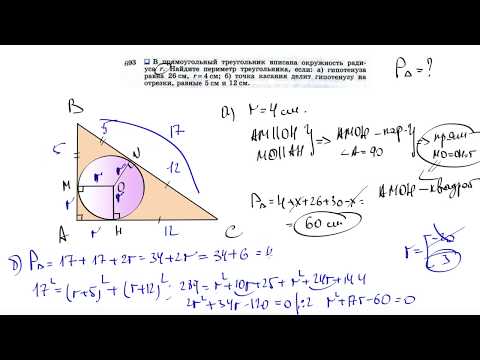
В треугольник вписана окружность радиуса 4 см?
Геометрия | 5 — 9 классы
В треугольник вписана окружность радиуса 4 см.
Найдите длины сторон треугольника, если одна из них разделена точкой касания на отрезки длиной 4 см и 5 см.
Из за того, что один из отрезков равен радиусу, угол треугольника с вершиной в конце этого отрезка — прямой (там получается ромб из 2 отрезков касательных и из 2 радиусов, ясно что это квадрат, поскольку углы между касательными и радиусами в точки касания прямые).
Для прямоугольного треугольника стороны a = 4 + 5 = 9 ; b = x + 4 ; c = x + 5 ; связаны теоремой Пифагора.
(x — единственный неизвестный из отрезков, на которые точки касания вписанной окружности делят стороны)
(x + 4) ^ 2 + 9 ^ 2 = (x + 5) ^ 2 ;
4 ^ 2 + 9 ^ 2 — 5 ^ 2 = 2 * x ;
Стороны 9, 40, 41, это известная Пифагорова тройка (наподобие 3, 4, 5 или 5, 12, 13).
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

Точка касания окружности, вписанной в прямоуугольный треугольник, делит гипотенузу на отрезки, равные 8 и 12?
Точка касания окружности, вписанной в прямоуугольный треугольник, делит гипотенузу на отрезки, равные 8 и 12.
Найдите радиус этой окружности.
Видео:Геометрия К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 смСкачать

В равнобедренный треугольник вписана окружность радиус которой равен 10 точка касания делит боковую сторону на отрезки длины которых относятся как 8 : 5 считая от вершины равнобедренного треугольника ?
В равнобедренный треугольник вписана окружность радиус которой равен 10 точка касания делит боковую сторону на отрезки длины которых относятся как 8 : 5 считая от вершины равнобедренного треугольника найдите площадь этого треугольника.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Окружность, вписанная в треугольник, делит точкой касания гипотенузу на отрезки 12 и 5?
Окружность, вписанная в треугольник, делит точкой касания гипотенузу на отрезки 12 и 5.
Найдите радиус окружности.
Видео:Задание 26 Окружность Равнобедренный треугольникСкачать

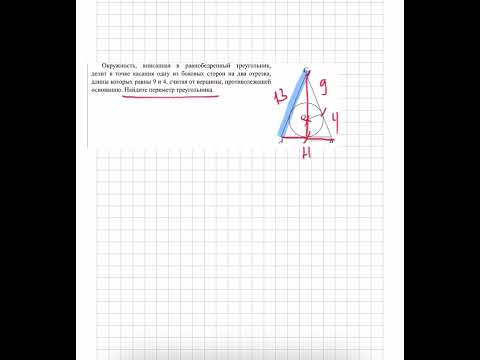
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию?
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию.
Найдите периметр треугольника.
Видео:Планиметрия 28 | mathus.ru | Радиус окружности, вписанной в равнобедренный треугольникСкачать

Ребят, помогите, пожалуйста?
Ребят, помогите, пожалуйста!
В треугольник вписана окружность радиуса 2.
Одна из сторон треугольника делится точкой касания на отрезки длиной 7 и 2.
Найдите радиус окружности, описанной около треугольника.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 4, считая от вершины, противолежащей основанию?
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 4, считая от вершины, противолежащей основанию.
Найдите периметр треугольника.
Видео:Радиус описанной окружностиСкачать

В прямоугольном треугольнике точка касания вписанной в него окружности и гипотенузы делит гипотенузу на отрезки, длины которых равны 3 и 7, найдите площадь треугольника?
В прямоугольном треугольнике точка касания вписанной в него окружности и гипотенузы делит гипотенузу на отрезки, длины которых равны 3 и 7, найдите площадь треугольника.
Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

В треугольник с периметром, равным 84, вписана окружность?
В треугольник с периметром, равным 84, вписана окружность.
Одна из точек касания делит сторону треугольника на отрезки с длинами 12 и 14.
Найдите площадь треугольника.
Видео:ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

В треугольник, стороны которого равны 6, 9, 11, вписана окружность?
В треугольник, стороны которого равны 6, 9, 11, вписана окружность.
Найдите длины отрезков этих сторон, на которые они делятся точками касания с вписанной окружностью.
Видео:№707. Угол, противолежащий основанию равнобедренного треугольника, равен 120°, боковая сторонаСкачать

Одна из сторон треугольника равно 30 см, а другая сторона делится точкой касания вписанной окружности на отрезки длиной 12 см и 14 см, считая от конца неизвестной стороны?
Одна из сторон треугольника равно 30 см, а другая сторона делится точкой касания вписанной окружности на отрезки длиной 12 см и 14 см, считая от конца неизвестной стороны.
Найти радиус вписанной окружности.
На этой странице находится вопрос В треугольник вписана окружность радиуса 4 см?, относящийся к категории Геометрия. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Геометрия. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.