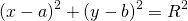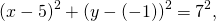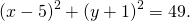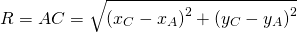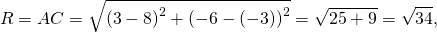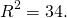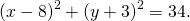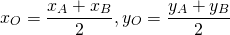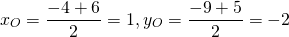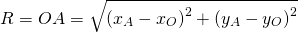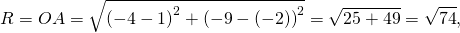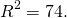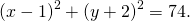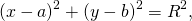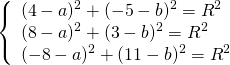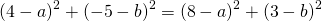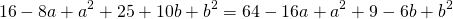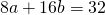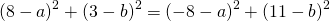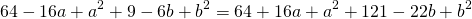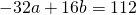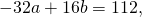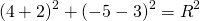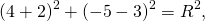Дана точка 4 6 написать уравнение окружности с диаметром оа (5 видео)

Помогите пожалуйста решить задачу: Дана точка (-4;6) Написать уравнение окружности, диаметром которой служит отрезок ОА

Вообще неправильно вы ей тут говорите. Как бы точка О может лежать хоть где, как бы в задании не сказано, что т. О находится на пересечении осей координат. Плюсом еще вы подставляете какие-то левые координаты .

1. найти середину ОА

2. найти длину ОА
3. (х-Хсередины оа) ^2+(y-Y середины oa)^2=половина длины ОА ^2

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Дана точка 4 6 написать уравнение окружности с диаметром оа

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.