Доказательство теоремы разности векторов

Определение 12. Разностью Двух векторов A и B, называются такой третий вектор С, обозначаемый символом A — B, при сложении которого с вектором B получаем вектор A.

Теорема 7. Для любых векторов A, B Разность A — B существует, единственна и вычисляется по формуле:

Доказательство. Так как

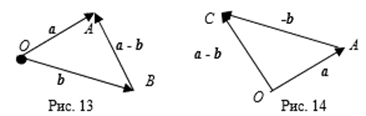
Разность векторов A И B геометрически можно найти двумя способами по определению 12 (см. рис. 13) и по теореме 7 (см. рис 14). По определению 12 разность A — B равна вектору, выходящему из конца второго вектора B в начало первого A, если векторы A И B отложены от одной точки. По теореме 7 разность A — B равна сумме векторов A + (-B).

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вычитание векторов. Как найти разность векторов

Вы будете перенаправлены на Автор24

Видео:Вычитание векторов. 9 класс.Скачать

Откладывание вектора от данной точки

Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Введем следующую теорему:

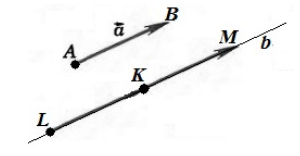
От любой точки $K$ можно отложить вектор $overrightarrow$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

В этом случае, очевидно, что искомый вектор — вектор $overrightarrow$.

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Видео:РАЗНОСТЬ ВЕКТОРОВ геометрия 9 АтанасянСкачать

Вычитание векторов. Правило первое

Пусть нам даны векторы $overrightarrow$ и $overrightarrow$.

Готовые работы на аналогичную тему

Построение разности двух векторов рассмотрим с помощью задачи.

Решение.

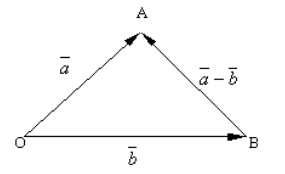
Рисунок 3. Разность двух векторов

По правилу треугольника для построения суммы двух векторов видим, что

Из определения 2, получаем, что

Видео:Построить разность векторов.Скачать

Вычитание векторов. Правило второе

Вспомним следующее необходимое нам понятие.

Вектор $overrightarrow$ называется произвольным для вектора $overrightarrow$, если эти векторы противоположно направлены и имеют равную длину.

Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.

Доказательство.

По определению 2, имеем

Прибавим к обеим частям вектор $left(-overrightarrowright)$, получим

Так как векторы $overrightarrow$ и $left(-overrightarrowright)$ противоположны, то $overrightarrow+left(-overrightarrowright)=overrightarrow$. Имеем

Теорема доказана.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Пример задачи на понятие разности векторов

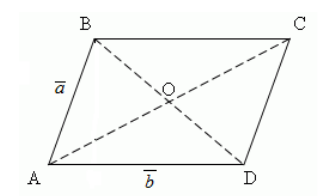
Рисунок 4. Параллелограмм

Решение.

а) Произведем сложение по правилу треугольника, получим

Из первого правила разности двух векторов, получаем

б) Так как $overrightarrow=overrightarrow$, получим

По теореме 2, имеем

Используя правило треугольника, окончательно имеем

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 04 2022

Видео:Доказательство теоремы о разложении вектора (геометрия 9 класс)Скачать

Геометрия, 9 класс, урок: «Вычитание векторов»

ГЕОМЕТРИЯ, 9 КЛАСС, УРОК: «ВЫЧИТАНИЕ ВЕКТОРОВ»

Тема: Вычитание векторов

Знать, какой вектор является разностью двух векторов, теорему о разности векторов.

Уметь строить разность двух векторов двумя способами, применять эти знания при решении задач.

I. Организационный момент: назвать уели урока.

II. Проверка пройденного материала:

1. Как называются векторы, имеющие равные модули и противоположно направленные?

Б) противоположно направленные

2. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?

А)

Б)

В)

3. Закончите предложение:

Суммой двух векторов называется вектор, построенный по правилу. (треугольника)

4. Вставьте пропущенное слово:

Чтобы сложить два неколлинеарных вектора и, нужно отложить от произвольной точки О векторы = и = и построить. ОАСВ, тогда =+

5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом.

III. Объяснение нового материала:

Вычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку

=+. Итак, == — = — .

Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:

а — b = а + (- b), где числа b и + (- b) — противоположные.

Итак, нам надо доказать, что результат вычитания вектора из вектора тот же, что и результат сложения векторов а + (- b).

2. Теорема о разности двух векторов.

Теорема (о разности векторов)

Для любых векторов и справедливо равенство — = + (- ).

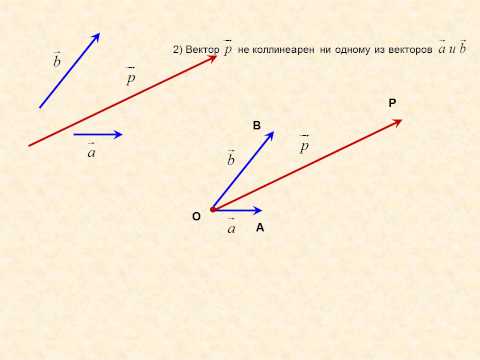
Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда, согласно определению, разность векторов и есть вектор , т. е. = — = — . По правилу треугольника = + . Кроме того, = — = —. Поэтому — = = + = (-) + =+(-)=+(-). Теорема доказана.

3. Построение разности векторов.

Доказанная теорема подсказывает еще один способ построения разности векторов и .

Отложим от произвольной точки О отложим вектор = , затем от точки А отложим вектор = —. Тогда по теореме о разности двух векторов — = + (-), поэтому — = + = . Итак, мы построили разность векторов и .

Выводы по уроку:

1. Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор .

2. Теорема ( о разности двух векторов): Для любых векторов и справедливо равенство:

— = + (-).

IV. Закрепление полученных знаний.

А) Разностью двух векторов и называется такой вектор , построенный по правилу треугольника.

Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений

В) Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор

2. Какой вектор, изображенный на рисунке, является разностью векторов и ?

А)

Б)

В)

3. № 000. Дан треугольник АВС. Выразите векторы = и = вектор .

а) —

б) —

в) +

4. № 000. Сторона равностороннего треугольника АВС равна а. Модуль ½ — ½ = а

V. Подведение итогов.

VI. Задание на дом: п.82, №№ 000, 756, 767

📹 Видео

Геометрия 9 класс (Урок№3 - Вычитание векторов)Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Координаты вектора. 9 класс.Скачать

Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

10 класс, 40 урок, Сложение и вычитание векторовСкачать

Математика это не ИсламСкачать

Теорема Штейнера - доказательствоСкачать

9 класс, 2 урок, Координаты вектораСкачать

Сложение векторов. 9 класс.Скачать

РАЗБИРАЕМ ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ II 😊#shorts #математика #егэ #задачи #егэ2022 #огэ2022Скачать

8 класс, 46 урок, Вычитание векторовСкачать

9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

СУММА ВЕКТОРОВ правило треугольникаСкачать

Вычитание векторов. Практическая часть. 9 класс.Скачать