Вектор силы под углом

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Вектор силы под углом

1. Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.

2. Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.

3. Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.

Краткая теория:

Ввиду того, что сила — вектор, вычитание сил проводится по правилам, принятым для векторов. Пусть надо вычесть силу F2 из силы F1.

Параллельным переносом начало силы F2 совмещаем с началом силы F1.

Из конца вектора F2 проводим вектор в конец вектора F1. Направление — от F2 к F1. Это и есть разность.

Разложение силы на составляющие по направлениям — операция, обратная нахождению равнодействующей. Технически она выполняется переносом направлений. Сумма составляющих должна давать исходный вектор.

Пусть задан вектор силы F. Надо разложить его на составляющие по заданным направлениям A и B.

Перенесем линии направлений A и B так, чтобы они прошли через конец вектора F. В полученной фигуре мы легко узнаем параллелограмм сил, построенный на составляющих FA и FB.

Проекции сил на оси координат можно считать частным случаем разложения на заданные направления. Оси координат, как правило, мы выбираем прямоугольными, что облегчает задачу. Проекции получают опусканием перпендикуляров на заданные оси координат. Проекции — скалярные величины, то есть они не имеют направления. Но каждой проекции приписывается знак «+» или «-«, в зависимости от направления исходного вектора относительно выбранных направлений осей.

Задан вектор силы F. Надо найти его проекции на выбранные оси прямоугольной системы координат.

Опускаем перпендикуляры на оси. Получаем проекции.

Формулы для решения:

где «альфа» — угол между вектором F и осью X.

Где «альфа» — угол между векторами

Алгоритм решения типовой задачи:

1. Кратко записываем условие задачи.

2. Изображаем условие графически.

3. Проводим графическое построение.

4. Проводим аналитический расчет.

5. Подставляем величины в общее решение, вычисляем.

6. Записываем ответ.

Примеры решения:

Задача 1.

Найти разность двух сил 5 и 10 ньютонов, направленных под углом 45 градусов друг к другу.

1. Кратко записываем условие задачи. Отметим, что в условии не сказано, какой вектор — уменьшаемое, а какой — вычитаемое. Поэтому разберем оба случая

а) Из первого вектора вычитается второй.

2. Изображаем условие графически.

3. Проводим графическое построение.

4. Проводим аналитический расчет.

5. Подставляем величины в общее решение, вычисляем.

Направление — от второго вектора к первому.

б) Из второго вектора вычитается первый

2. Изображаем условие графически.

3. Проводим графическое построение.

4,5. Проведение аналитического расчета и вычислений такое же, как и выше, но направление вектора разности — противоположное.

6. Ответ: Вектор разности в обоих случаях имеет величину 9,45 Н, направление в первом случае от второго вектора к первому, во втором случае — наоборот.

Задача 2.

Канатоходец прогибает канат своим весом, равным 60 кг. Определить силу натяжения троса, если угол прогиба 120 градусов.

1. Кратко записываем условие задачи.

2. Изображаем условие графически.

3. Проводим графическое построение. Равнодействующая двух сил «T» должна уравновешивать силу «F».

4. Проводим аналитический расчет. Треугольники, на которые разделился параллелограмм сил — равносторонние, так как они равнобедренные по построению, а вектор «F» делит угол пополам, то есть угол при основании равен 60 градусам. Таким образом, каждая из сил «T» равна силе «F».

5. Подставляем величины в общее решение, вычисляем.

T=60 кг. Переводим в систему СИ. В одном килограмме 9,8 ньютона. Поэтому:

6. Ответ: Сила натяжения троса 60 кг или 591 ньютон.

Задача 3.

Найти проекции силы 150 ньютонов на координатные оси прямоугольной системы координат, если вектор силы направлен под углом 30 градусов к оси абсцисс.

1. Кратко записываем условие задачи.

2. Изображаем условие графически.

3. Проводим графическое построение.

4. Проводим аналитический расчет.

5. Подставляем величины в общее решение, вычисляем.

6. Ответ: Проекция на ось абсцисс равна 129,5 ньютона, проекция на ось ординат равна 75 ньютонов.

Видео:Равнодействующая и сложение силСкачать

Вращательный момент, примеры расчетов

Рассмотрим несколько задач на тему «вращательный момент» с пояснениями. Будем осуществлять расчет перпендикулярных частей сил и плеч сил в случаях, когда углы между силой и рычагом отличаются от прямого.

Это вторая часть статьи о моменте силы. Первая часть находится тут (откроется в новой вкладке).

Видео:Как проецировать вектор сил на оси | ЕГЭ Физика | Николай Ньютон. ТехноскулСкачать

Угол между силой и рычагом отличается от прямого

Рассмотрим рисунок 1. На рисунке 1а сила приложена к рукоятке ключа под прямым углом. На рисунках 1б и 1в углы между силой и рукояткой (рычагом) отличаются от прямого.

Длина рычага является расстоянием между точкой приложения силы и осью вращения. Когда угол отличается от прямого, для вычисления момента силы нужно раскладывать на проекции либо силу, либо длину рычага (рукоятки).

Видео:Как разложить силы на проекции (динамика 10-11 класс) ЕГЭ по физикеСкачать

Раскладываем силу

Разложим приложенную силу ( F ) на части. Одна часть будет располагаться перпендикулярно рукоятке, а другая – параллельно (см. рис. 2).

Рукоятку вращает только перпендикулярная часть силы. На рисунке 2 она обозначена, как ( F_ ).

Параллельная рукоятке часть обозначена ( F_ ). Она не вращает рукоятку, а сдвигает ключ либо от гайки (рис. 2а), либо в сторону гайки (рис 2б).

Рукоятка ключа – это плечо для перпендикулярной части силы.

Момент силы для рисунка 2 считаем по формуле:

Наиболее выгодно прикладывать силу перпендикулярно рукоятке (см. рис 1а). В этом случае вращательный момент силы будет наибольшим.

В остальных случаях вращать рукоятку будет не вся сила целиком, а только лишь ее перпендикулярная часть.

Помним! Между силой и ее плечом угол прямой.

Задача 1

Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить часть вектора силы, вращающего гаечный ключ. С помощью этой части вектора силы рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.

Решение:

• Проведем перпендикулярную ( F_ ) часть и параллельную рычагу ( F_ ) часть силы (рис. 3).

Примечание:

Чтобы разложить вектор силы на части, нужно нарисовать прямоугольник. Так, чтобы вектор, который мы раскладываем, оказался диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны рукоятке, а другие две – перпендикулярны ей.

Тогда стороны прямоугольника обозначат проекции – перпендикулярную и продольную (параллельную).

• Вычислим перпендикулярную ( F_ ) часть силы:

[ F_ = F cdot sin(alpha)]

( F_ = 10 left(Hright))

• Рассчитаем теперь вращательный момент M этой силы:

( M = 2 left( H cdot text right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text right) )

Видео:Построение проекции вектора на осьСкачать

Раскладываем расстояние

Для подсчета вращательного момента, на проекции можно раскладывать не только силу.

На части можно разложить длину рукоятки, так, чтобы одна часть оказалась продольной силе, а другая – параллельной (рис. 4).

После выбираем часть длины, перпендикулярную силе. Эта сторона является плечом силы.

На рисунке 4а перпендикулярно силе располагается ( d_ ), для этого случая момент силы считаем так:

Из рисунка 4б выбираем перпендикулярную силе величину ( d_ ). Момент силы вычисляем, пользуясь формулой:

Задача 2

Угол между приложенной силой и рукояткой ключа равен 30 градусам. Определить плечо вектора приложенной силы. С помощью этого плеча рассчитать вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.

Решение:

• Проведем параллельную ( d_ ) и перпендикулярную силе ( d_ ) часть рычага (рис. 5).

Примечание:

Снова рисуем прямоугольник. Но теперь не сила, а рукоятка должна оказаться диагональю прямоугольника. Две стороны этого прямоугольника будут параллельны силе, а другие две – перпендикулярны ей.

В прямоугольнике выбираем сторону, перпендикулярную силе. Эта сторона является плечом силы.

О формулах разложения векторов на проекции подробно написано тут (откроется в новой вкладке).

• Вычислим перпендикулярную силе F часть длины ( d_ ) рычага – плечо силы F:

[ d_ = d cdot sin(alpha)]

( d_ = 0,1 left( text right))

• Рассчитаем теперь с помощью найденного плеча ( d_ ) силы F вращательный момент M:

( M = 2 left( H cdot text right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text right) )

Видео:Тренировочные задания по теме: "Результирующая сила"Скачать

Расчет момента силы с помощью формулы, содержащей угол между силой и рычагом

Вращательный момент можно рассчитать без прямого указания плеча силы, зная угол между силой и рычагом. Подробнее в первой части статьи (откроется в новом окне)

Задача 3

Угол между приложенной силой и рукояткой ключа равен 30 градусам. Не рассчитывая плеча силы найти вращательный момент. Сила равна 20 Н. Длина рукоятки 20 см.

Решение:

• Воспользуемся формулой для вычисления вращательного момента:

[ M = F cdot d cdot sin(alpha)]

( M = 20 cdot 0,2 cdot 0,5)

( M = 2 left( H cdot text right) )

Ответ: Вращательный момент равен ( 2 left( H cdot text right) )

Как видно из задач 1 — 3, все три способа вычисления вращательного момента дают аналогичные результаты.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Видео:Движение тела, брошенного под углом к горизонтуСкачать

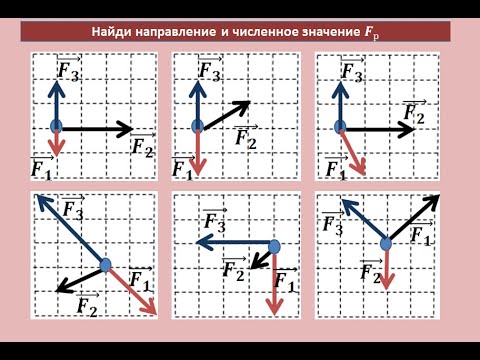
Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Видео:ЕВГЕНИЯ ЛЕВАШОВА-ЕЛАГИНА: зависимость, абьюз, эстетика clean girl и идеальный мужчина!Скачать

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2 -х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

📽️ Видео

Андрей Илларионов. Запад и НезападСкачать

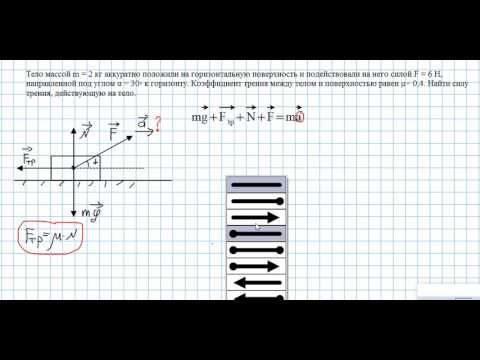
Физика | Ликбез по векторамСкачать

Урок 9. Проекции вектора на координатные осиСкачать

сила под угломСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

Правильная уникальная техника приседаний, о которой никто не расскажетСкачать

Кинематика: Тело, брошенное под углом к горизонтуСкачать

Наклонная плоскость. Расстановка сил | 50 уроков физики (6/50)Скачать

Модуль 2. Баллистика. Равноускоренное движение в плоскости.Скачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать