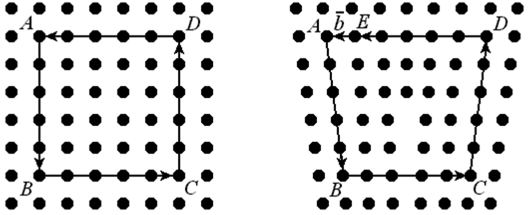
Вектор сдвига и вектор бюргерса (3 видео)

Контур и вектор Бюргерса

При рассмотрении теории дислокаций часто используют понятия контура Бюргерса и вектора Бюргерса.

Контур Бюргерса представляет собой замкнутый контур, проведенный в кристалле в области неискаженного материала и охватывающий линейный дефект решетки. На рис. 8.5 показано построение этого контура в совершенном кристалле, не имеющем дислокаций. За исходную точку принят атом А. двигаясь вниз на пять межатомных расстояний, в точке В повернем направо и пройдем такой же отрезок в пять шагов (до узла С), а затем поднимемся до узла D (вновь то же расстояние) и вернемся к исходному атому А. в результате такой процедуры получится замкнутый контур.

Рис. 8.5. Контур Бюргерса в совершенном кристалле (а), в кристалле, содержащем дислокацию (б)

Построим теперь аналогичный контур в кристалле, содержащем дислокацию (рис. 8.5 б). если полностью повторить предыдущий путь при движении от узла А через позиции B, C, D, то легко видеть, что контур окажется незамкнутым. Чтобы вернуться в исходный узел А, требуется совершить еще один шаг на величину межатомного расстояния. Иными словами, для замыкания контура нужен отрезок ЕА. Вектор b, проведенный из узла Е в узел А и замыкающий контур, называется вектором Бюргерса. Таким образом, дислокацию можно охарактеризовать не только как границу незавершенного сдвига, но и как одномерный дефект, для которого вектор Бюргерса отличен от нуля. Вектор Бюргерса показывает величину и направление сдвига, вызванного движением дислокации. Он считается важной количественной характеристикой дислокации, которая определяет энергию дислокации, является показателем упругих искажений решетки, создаваемых этим дефектом и мерой ее подвижности.

Можно также отметить, что вектор Бюргерса рассматривается и как трансляционный вектор, так как перенос на его величину и по его направлению переводит кристалл в положение самосовпадения – после завершения сдвига на величину вектора b прежняя конфигурация атомов в решетке полностью восстанавливается.

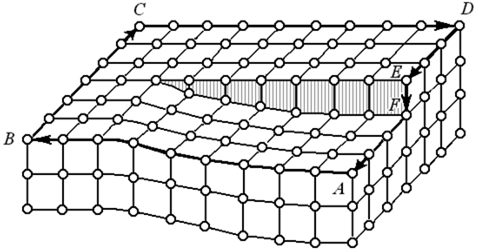
Построение контура и вектора Бюргерса для винтовой дислокации показано на рис. 8.6. За начало отсчета принят узел А. Построим контур путем последовательного перемещения по поверхности кристалла, имеющего винтовую дислокацию. В этом случае при достижении позиции Е необходимо будет сместиться вниз на одно межатомное расстояние (EF), чтобы иметь возможность вернуться в исходную точку А. При построении аналогичного контура в бездефектном кристалле дополнительного шага совершать не придется. Тем самым при обходе контура Бюргерса в кристалле, имеющем винтовую дислокацию, отрезок EF, параллельный линии l этой дислокации, будет отражать ее вектор Бюргерса.

Рис. 8.6. Контур Бюргерса вокруг винтовой дислокации

Поскольку любая дислокация является границей зоны сдвига, то она не может обрываться внутри кристалла. Дислокация в состоянии лишь выходить своими концами на поверхность, разветвляться на несколько дислокаций, образующих узел или формировать замкнутое кольцо, полностью расположенное в кристалле. Учитывая, что дислокационная линия в общем случае может иметь произвольную кривизну, то вводится понятие о смешанной дислокации, имеющей различную долю краевой и винтовой компонент. Таким образом, любую произвольную линию дислокации можно разделить на краевую и винтовую составляющие.

Содержание

Вектор Бюргерса и его свойства
Методическое пособие (стр. 5 )
14.3. § 2. КЛАССИФИКАЦИЯ ДЕФЕКТОВ.
14.4. § 4. ТИПЫ ТОЧЕЧНЫХ ДЕФЕКТОВ. ДЕФЕКТЫ ФРАНКЕЛЯ И ШОТТКИ.
14.5. § 12. ОПРЕДЕЛЕНИЕ ДИСЛОКАЦИИ. КОНТУР БЮРГЕРСА И ВЕКТОР БЮРГЕРСА.
14.6. § 13. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ДИСЛОКАЦИИ. КРАЕВЫЕ И ВЕНТОВЫЕ ДИСЛОКАЦИИ.
14.7. §14. ДИСЛОКАЦИИ В НЕПРЕРЫВНОЙ УПРУГОЙ СРЕДЕ.
14.8. § 21. РАСЩЕПЛЕНИЕ ДИСЛОКАЦИИ И ДЕФЕКТЫ УПАКОВКИ.
15. термопара
15.1. ГЛАВА IX
ТЕРМОЭЛЕКТРИЧЕСКИЕ И ГАЛЬВАНОМАГНИТНЫЕ ЯВЛЕНИЯ
15.2. § 79. ЭФФЕКТ ЗЕЕБЕКА.
📹 Видео

Видео:Занятие 12. Векторы и матрицыСкачать

Вектор Бюргерса и его свойства

Важнейшей характеристикой дислокации является вектор Бюргерса Ь, характеризующий степень искаженное™ кристаллической решетки вокруг дислокации. Он определяет тип дислокации, ее энергию, силу, действующую на дислокацию, величину связанного с дислокацией сдвига.

Для графического определения вектора Бюргерса дислокации проводят следующее геометрическое построение (рис. 2.21). Вокруг данной дислокации (положение ее оси обозначено как CD, точка D находится за плоскостью чертежа), начиная, например, от атома А, проводят произвольный замкнутый контур (контур Бюргерса), переходя последовательно от атома к атому. Такой контур вокруг краевой дислокации, расположенной перпендикулярно плоскости чертежа, показан на рис. 2.21, а.

Рис. 2.21. Построение контура Бюргерса для краевой дислокации: а — реальный кристалл с дислокацией (CD — ось дислокации); б — идеальный кристалл; b — вектор Бюргерса краевой дислокации

Затем точно такой же путь необходимо пройти в идеальном кристалле без дислокации (рис. 2.21, б). Как видно из рис. 2.21, б, контур Бюргерса в идеальном кристалле оказался незамкнутым (имеет невязку А В). Вектор

Ь, который необходим для того, чтобы замкнуть контур, и есть вектор Бюргерса. Видно, что вектор Бюргерса краевой дислокации перпендикулярен линии дислокации. Такой вектор показан также на рис. 2.19.

Схема построения контура Бюргерса для винтовой дислокации представлена на рис. 2.22. Определение вектора Бюргерса винтовой дислокации проводится аналогично тому, как это выполнялось для краевой дислокации. Из рисунка 2.22 видно, что вектор Бюргерса винтовой дислокации параллелен линии дислокации (см. также рис. 2.20).

Свойства вектора Бюргерса. Важнейшее свойство вектора Бюргерса заключается в том, что он является инвариантом дислокации, т. е. остается постоянным вдоль всей линии дислокации (хотя ориентация дислокации в различных ее участках может меняться) и сохраняется по величине и направлению при движении дислокации. Из условия инвариантности вектора Бюргерса следует, что дислокация не может обрываться внутри кристалла. Она должна выходить на поверхность кристалла (либо на границу зерна, субзерна), или образовывать замкнутую петлю, или переплетаться с другими дислокациями, образуя дислокационные узлы и дислокационную сетку. При этом, если три или более дислокации встречаются в точке или узле, необходимым условием является равенство нулю суммы векторов Бюргер- са этих дислокаций. Как уже отмечалось, вектор Бюргерса перпендикулярен линии краевой дислокации и параллелен линии винтовой дислокации, а с линией смешанной дислокации (см. далее) образует произвольный угол в различных ее точках.

Рис. 2.22. Схема построения контура Бюргерса для винтовой дислокации: а — реальный кристалл с дислокацией (I — ось дислокации); б — идеальный кристалл;

Ь — вектор Бюргерса винтовой дислокации

Отличительным свойством вектора Бюргерса является то, что для дефектов недислокационного типа (например, точечных дефектов, цепочек вакансий или междоузельных атомов) он равен нулю; он отличен от нуля только для дислокаций. Исходя изданного обстоятельства, а также учитывая, что дислокации в кристаллах не всегда создаются путем сдвига (см. далее), можно дать общее определение дислокации как линейного дефекта кристаллической решетки, для которого контур Бюргерса имеет отличную от нуля невязку.

Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

Методическое пособие (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6

Однако этот метод дает лишь усредненные по макроскопическому объему кристалла данные и не позволяет установить, каковы смещения отдельных атомов из по

ложений, требуемых идеальной структурой (1.1), в тех местах, в которых при пластической деформации эта структура нарушается. Лишь в последние годы удалось выяснить, какие дифракционные эффекты вызывают дефекты решетки различных типов.

14.3. § 2. КЛАССИФИКАЦИЯ ДЕФЕКТОВ.

Простая геометрическая классификация дефектов основана на числе измерений, в которых связанные с дефектом искажения решетки, нарушающие ее периодичность, простираются на макроскопические расстояния. Макроскопическими будем называть такие расстояния, которые значительно превосходят расстояние r0 между соседними атомами в кристалле. Расстояния, сравнимые-с r0, называются микроскопическими.

Проиллюстрируем предлагаемую классификацию в случае простой кубической решетки. Примером нульмерного, или точечного, дефекта является вакансия. Атомная плоскость с вакансией представлена на рис. 4,а. В бездефектной решетке равновесное межатомное расстояние r0 соответствует равенству сил отталкивания и притяжения между атомами. Удаление атома нарушает этот баланс сил. Поскольку силы отталкивания возрастают при уменьшении межатомного расстояния по сравнению с равновесным (r r0) атомная конфигурация в какой-либо точке его края не зависит от R (рис. 5, б), а в средней части диска нормальная структура кристалла восстановилась, осталось лишь небольшое упругое растяжение решетки. Представленная на рис. 5,в конфигурация отвечает атомной полуплоскости, обрывающейся в кристалле вдоль некоторой линии (в данном случае вдоль края диска). Так как R>r0, то получившийся дефект имеет в одном измерении (вдоль периметра диска) макроскопические размеры и является поэтому одномерным или линейным дефектом. Он называется краевой дислокацией (см. § 12). Из рис. 5,0 видно, что в двух других измерениях (в плоскости рисунка) взаимное расположение атомов уже на малом расстоянии от края обрывающейся плоскости мало отличается от характерного для простой кубической решетки и дефект имеет микроскопические размеры.

Чтобы получить пример двухмерного (поверхностного) дефекта, повторим проделаннoе построение для ГЦК-решетки. ГЦК-решетку можно представить как плотнейшую упаковку слоев из атомов-шаров, расположенных в кристаллографических плоскостях . Атомы одного такого слоя представлены на рис. 6 сплошными кружками. Их центры располагаются в узлах решетки, которые обозначим буквой Л, а весь слой атомов назовем слоем Л. Между атомами Л находятся лунки двух сортов, отмеченные точками (В) и крестиками (С). Укладку второго слоя шаров можно начать, поместив первый шар в лунку В или С. Но после этого все остальные шары второго слоя займут тоже только лунки В или только лунки С. Предположим для определенности, что заняты лунки В и назовем этот слой слоем В. Два ряда атомов этого слоя показаны пунктиром. Начиная укладку третьего слоя, можно первый атом поместить в лунку, образовавшуюся над лункой С первого слоя, либо в лунку А над центром атома первого слоя. Однако, как видно из рис. 7, ГЦК-решетка получится только, если атом третьего слоя поместить в лунку С. Если его поместить в лунку А, то получится чередование слоев, характерное для гексагональной плотноупакованной (ГПУ) решетки. Наконец, атомы четвертого слоя в ГЦК-решетке попадают в лунки A и располагаются точно над — атомами первого слоя. Порядок чередования атомных

6. Атомные слои в ГЦК-ре-

сплошные кружки — слой А, пунктирные — слой В, крестики — центры атомов слоя С

слоев в ГЦК-решетке описывается последовательностью. АВСАВСАВС. Для ГПУ-решетки имеем соответственно . АВАВАВАВ.

7. Элементарная ячейка ГЦК-решетки с выделенными плоскостями (111)

Пусть теперь, в одной из плоскостей ГЦК-решетки, например в плоскости С, образовалось плоское скопление вакансий настолько больших размеров, что (аналогично рис. 5, в) за счет релаксации решетки противолежащие берега диска, образуемые атомами в узлах В и Л, смыкаются. Тогда на месте изъятой плоскости С (см. стрелку) правильное чередование атомных плоскостей окажется нарушенным

Такое нарушение называется дефектом упаковки. В двух измерениях оно имеет макроскопические размеры. В направлении нормали к дефекту упаковки правильные атомные соседства начинаются уже со следующей атомной плоскости. Поэтому дефект упаковки является двухмерным дефектом решетки.

Другими двухмерными, или поверхностными, дефектами решетки являются межзеренные границы в поликристаллах, границы двойников и сегнетоэлектрических и ферромагнитных доменов, антифазные границы в упорядоченных сплавах, внешняя поверхность кристалла.

Наконец, трехмерным дефектом является всякое искажение кристаллической решетки, размеры которого во всех трех измерениях макроскопические. Сюда относятся включения с другой кристаллической структурой (выделения второй фазы), аморфные включения, нарушения сплошности кристалла (трещины, поры).

14.4. § 4. ТИПЫ ТОЧЕЧНЫХ ДЕФЕКТОВ. ДЕФЕКТЫ ФРАНКЕЛЯ И ШОТТКИ.

Согласно приведенной в гл. 1 классификации точечными дефектами называются нарушения периодической структуры решетки, размеры которых во всех измерениях не превосходят нескольких межатомных расстояний. Простейшими точечными дефектами являются вакансии (узлы, из которых удалены атомы) и межузельные атомы (рис. 8). К точечным дефектам в одноатомных кри-

9. Октаэдрическое и тетраэд-рическое междоузлия в ГЦК-решетке:

+ — октаэдрическое междоузлие. • — тетраэдрическое междоузлие

8. Схематическое изображение вакансии, межузельного атома и примесных атомов замещения и внедрения в плоскости (111) ГЦК-ре-шетки:

сталлах следует также отнести примесные атомы различных сортов, которые могут либо замещать атомы матрицы (примеси замещения), либо быть внедренными в различные междоузлия (примеси внедрения).

В кубических и гексагональных решетках существуют межузлия двух типов—более просторные октаэдрические и менее просторные тетраэдрические (рис. 9). Как собственные, так и примесные межузельные атомы могут располагаться в межузлиях обоих типов или образовывать с каким-либо атомом матрицы различные сложные конфигурации. Межузельные атомы иногда называют внедренными атомами или, кратко, внедрениями (англ. interstitials).

В результате удаления атома из своего узла в какое-либо межузлие возникает пара вакансия — межузельный атом, которая называется дефектом Френкеля или френкелевской парой.

В кристаллах со сложной элементарной ячейкой, содержащей атомы нескольких сортов, вакансии могут быть в узлах любого сорта, а в межузлиях разных типов могут находиться атомы также любого сорта. В ионных кристаллах образование вакансий путем удаления положительных ионов (катионов) вызывает появление результирующего отрицательного заряда кристалла. Соответственно образование анионных вакансий приводит к появлению положительного-заряда. Нейтральность кристалла сохраняется, если ионы не удаляются из кристалла, а перемещаются в межузлия (дефекты Френкеля), либо если (при одинаковой валентности ионов) анионные и катионные вакансии образуются в равных количествах (дефекты Шоттки).

Объединение двух вакансий с образованием бивакансии обычно сопровождается выигрышем энергии. Поэтому такие точечные дефекты устойчивы и встречаются в кристаллах, хотя и в меньшей концентрации, чем одиночные вакансии. Тривакансии и более крупные их скопления (кластеры) также наблюдаются и, как будет показано, влияют на некоторые свойства кристалла. Аналогичным образом межузельные атомы могут образовывать устойчивые пары и более крупные скопления.

Примесные атомы могут также образовывать комплексы, объединяясь между собой и с собственными дефектами матрицы —вакансиями и межузельными атомами.

14.5. § 12. ОПРЕДЕЛЕНИЕ ДИСЛОКАЦИИ. КОНТУР БЮРГЕРСА И ВЕКТОР БЮРГЕРСА.

Чтобы дать определение дислокации, нам придется провести некоторые геометрические построения, которые на первый взгляд могут показаться несколько искусст-венными. Однако без них трудно решить поставленную задачу.

Следуя Бюргерсу и Франку, рассмотрим участок атомной плоскости в кристалле. Для простоты выберем простую кубическую решетку. Построим на этом участке

18. Контур Бюргерса в кристалле бездефектном (а) и с дислокацией (б)

замкнутый контур, проходящий через узлы решетки, при чем обход по контуру ведется по направлению часовой стрелки. Пусть контур начинается в точке Л (рис. 18 состоит из четырех шагов вправо, приводящих в узел В четырех шагов вниз (узел С), четырех шагов влево (узел D) и четырех шагов вверх, после чего мы, очевидно, возвращаемся в узел Л. Контур замкнулся. Повторим построение такого же контура Бюргерса в плоскости, пересекающей край обрывающейся атомной полу плоскости (см. рис. 5,0 и 18,6) так, чтобы контур охватывал этот край. Чтобы избежать неуверенности в правильном выборе соседних узлов сверху и снизу, контур должен проходить достаточно далеко от крайнего атома экстраплоскости. Если начало контура выбрано, например в точке А (рис. 18,6), то это требование выполнено. Двигаясь вновь на четыре межатомных расстояния вправо, вниз, влево и вверх, мы теперь приходим в узел А не, совпадающий с узлом Л. Контур Бюргерса имеет невязку А’А. Вследствие упругой деформации решетки вблизи дислокации длина шага на рис: 18, б не равна длине шага в недеформированной решетке (рис. 18, а). Поэтому невязка А’А не равна в точности межатомному расстоянию a0 в недеформированной решетке. Она станет равной a0, если снять упругую деформацию, например проведя разрез на продолжении лишней полуплоскости (QS) и дать решетке срелаксировать. Вектор b соединяющий конечную точку A’ контура Бюргера с начальной Л в релаксированной решетке, называется вектором Бюргерса и является количественной характеристикой дислокации — линейного дефекта, охватываемого контуром Бюргерса. Таким образом, проведенное построение позволяет дать определение дислокации. Дислокацией называется линейный дефект решетки, для которого контур Бюргерса имеет отличную от нуля невязку*.

Как видно, знак b зависит от направления обхода по контуру Бюргерса, а оно, в свою очередь, определено однозначно только, если задано направление обхода вдоль линии дислокации, т. е. единичный вектор касательной к линии дислокации 1. Будем всегда считать, что вектор 1 направлен за плоскость чертежа, что изображено на рис 18,б значком x. Если изменить направление обхода вдоль дислокации, т. е. знак вектора 1, и повторить построение, изменится, очевидно, и направление Ь на противоположное. Как известно, вектор, знак которого зависит от направления некоторого обхода, называется аксиальным (в отличие от полярного вектора, не связанного таким условием). Вектор Бюргерса (подобно вектору напряженности магнитного поля) является аксиальным.

Итак, дислокация характеризуется двумя векторами Ь и 1. Плоскость, проходящая через Ь и 1, называется плокостью скольжения дислокации. Смысл этого названия выяснится ниже.

Из правила построения контура Бюргерса следует что модуль вектора Бюргерса равен одному из межатомных расстояний. Как показано в § 16, обычно |b| равен кратчайшему межатомному расстоянию. в решетке.

Область диаметром 2—3 межатомных расстояния, посредственно окружающая край экстраплоскости, где число ближайших соседей данного атома (координационное число) однозначно не определяется, называется ядром дислокации, а остальная часть кристалла, в которой если и имеются искажения идеальной структуры, то незначительные упругие, называется «хорошим материалом»*.

* Обратное утверждение не имеет силы: контур Бюргерса может быть замкнутым, но тем не менее содержать несколько дислокации, суммарный вектор Бюргерса которых равен нулю.

14.6. § 13. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ДИСЛОКАЦИИ. КРАЕВЫЕ И ВЕНТОВЫЕ ДИСЛОКАЦИИ.

Из правила построения контура Бюргерса следует ряд важных свойств дислокации.

1. Вектор Бюргерса остается постоянным при движении вдоль дислокации. В самом деле, любые два контура C1 и С2, охватывающие дислокацию, различаются контуром, который ее не охватывает и поэтому имеет нулевую невязку. Следовательно, у контуров C1 и С3 невязка одинаковая.

2. Дислокация не может обрываться в кристалле. Она может лишь выходить на поверхность кристалла, замыкаться самое на себя либо разветвляться на несколько дислокации, образующих узел (рис. 19).

19. Дислокация выходит на 20. Запрещенный обрыв дислока-

поверхность кристалла ции в кристалле (а). Сохране-

(а), образует замкнутую ние вектора Бюргерса в точке петлю

(б) или разветвляет — разветвления дислокации (б)

Векторы Бюр герса bi дислокации, выходящих из узла, удовлетворяют условию

Для доказательства первого утверждения предположим, что справедливо обратное. Дислокация пересекает плоскости Р1 и Р2 (рис. 20, а) и обрывается между плоскостями р2 и Р3. Построим контур Бюргерса в плоскости Р2 (рис. 18,б). По определению он имеет невязку b. Перенесем теперь этот контур Бюргерса атом за атомом в соседнюю плоскость Рз. Поскольку каждый атом в плоскости Р2 имеет справа в плоскости Рз одного и только одного соседа, в плоскости Рз получим точно такой же контур с таким же количеством шагов и с такой же невязкой A’A. Но по предположению дислокация не пересекает плоскости Рз, т. е. контур Бюргерса в этой плоскости не имеет невязки, что противоречит нашему построению. Следовательно, предположение об обрыве дислокации невозможно.

Для доказательства соотношения (13.1) рассмотрим узел дислокации Y, расположенный между плоскостями P2 и Рз (рис. 20,б). Направление обхода дислокации 1, 2, 3 указано стрелками, векторы Бюргерса равны при этом b1, b2, b3. Построим контур Бюргерса в плоскости P2. Его невязка равна по определению b1. Переместим этот. контур последовательно в плоскости Рз, P4 Р5. расширяя его в случае надобности, чтобы он всюду проходил по хорошему материалу. Как показано выше, его невязка при этом сохраняется равной bi, хотя контур теперь охватывает две дислокации 2 и 3. Разделим теперь площадь, охватываемую контуром — в плоскости Р5 на две части так, чтобы через одну часть проходила дислокация 2, а через другую — дислокация 3. Невязка контура, охватывающего первую часть площади, равна b2 а для второй—bз. Следовательно, невязка полного контура, охватывающего обе дислокации, с одной стороны, равна b2+bз, а с другой стороны, она равна b1. Таким образом,

Чтобы исключить неравноправность дислокации 1 в отношении направления обхода, изменим его на обратное. Соответственно изменится знак вектора Бюргерса b1. Теперь все дислокации выходят из узла Y и из (13.2) следует (13.1).

При построении рис. 18 предполагалось, что контур Бюргерса плоский и векторы b и l взаимно перпендикулярны. Такие дислокации называются краевыми. Однако взаимная ориентация векторов b и 1 может быть произ

21. Контур Бюргерса для винтовой дислокации:

вольной. В частности, дислокация, у которой b и 1 параллельны, называется винтовой. Расположение атомов в ядре винтовой дислокации и контур Бюргерса для нее представлены на рис. 21 (см. также рис. 33). Из него видно, Что после обхода по контуру Бюргерса мы приходим из начальной точки А в конечную А’, расположённую на одно межплоскостное расстояние «выше» вдоль оси винтовой дислокации. Повторив обход, мы продвинемся еще на одно межплоскостное расстояние в том же направлении. Видно, что кристалл с винтовой дислокацией представляет собой фактически одну единственную атомную плоскость, свернутую в виде винтовой лестницы.

Наконец, если b и 1 образуют произвольный острый или тупой угол, дислокация называется смешанной (имеет смешанную ориентацию).

Для винтовой дислокации (b || 1) плоскость скольжения однозначно не определена. Краевая дислокация обозначается значком ±, где горизонтальная черта обозначает плоскость скольжения, вертикальная — экстраплос-кость. Винтовая дислокация обозначается символом у Дислокации с вектором Бюргерса обратного знака изо бражаются как Т и у. Дислокации, векторы Бюргерса которых образуют острый угол, называются одноименными, а тупой—разноименными

14.7. §14. ДИСЛОКАЦИИ В НЕПРЕРЫВНОЙ УПРУГОЙ СРЕДЕ.

Как видно из рис. 18 и 21, вокруг дислокации кристаллическая решетка искажена, причем деформация убывает по мере удаления от ядра и внеядра настолько мала, что может быть вычислена в приближении линейно теории упругости. Такая задача была решена Вольтерр

еще в 1907 г. Мы ее рассмотрим в следующем простом варианте, пренебрегая краевыми эффектами. Дан цилиндр радиусом R (рис. 22, а). Вырежем из него коаксиальный цилиндр радиусом ro 0 в формулах типа (14.2).

Выражение для смещения (20.28) позволяет вычислить и остальные упругие характеристики дислокации, в частности энергию одного атомного ряда W(x) и ее изменение W(x, а) при смещении верхней — половины кристалла относительно нижней на расстояние ab. Энергия дислокации W (а) получается суммированием W(X, а) по всем атомным рядам х=тЬ и x=(m+1/2)b соответственно в нижней и верхней половинах кристалла и есть, очевидно, периодическая функция. Вычисления дают [4]

Периодически изменяющуюся энергию кристалла c дислокацией при ее перемещении в плоскости скольже-ния называют пайерлсовским рельефом кристалла. Oн состоит из канавок и разделяющих их горбов. Напряжение op, необходимое для преодоления потенциального барьера в (20.31), называется напряжением Пайерлса:

Сходство выражений (20.28) и (20.32) с (20.10) и (20.21) показывает, что несимметричность атомной модели Френкеля — Конторовой не приводит к качественно отличным от полученных в симметричной континуальной модели Пайерлса результатам.

14.8. § 21. РАСЩЕПЛЕНИЕ ДИСЛОКАЦИИ И ДЕФЕКТЫ УПАКОВКИ.

Длина вектора Бюргерса не может быть меньше межатомного расстояния в решетке. В противном случае вдоль плоскости разреза на рис. 23 не будет восстановлена структура бездефектного кристалла. Посмотрим, однако, что получится, если вдоль части АА’ плоскости разреза совершить сдвиг на вектор b’, меньший вектора b решетки (рис. 43), а вдоль оставшейся части ВА разреза — на вектор b. Тогда линия A будет границей площади, по которой прошел сдвиг b, а линия А’ — граница сдвига b’. Таким образом, на линии A* имеет место скачок вектора сдвига на b»=b—b’ и дислокация с вектором Бюргерса b расщепилась на две с векторами Бюргерса b’ и b». Дислокации, у которых вектор Бюргерса меньше вектора решетки, называются частичными дислокациями. Мы их будем обозначать символами _| и [_ независимо от ориентации. Построение контура Бюргерса для частичной дислокации дано на рис. 46.

43. Расщепленная дислокация

В непрерывной упругой среде расщепление дислокации на частичные энергетически выгодно, ибо энергия Gb2>Gb/2+Gb//2 полной дислокации больше суммы энергий частичных. В кристалле же на полосе AA/ ширины правильная структура решетки нарушена; Возможно, однако, что симметрия решетки допускает на поверхности ЛЛ’ укладку атомов, которая хотя и отличается от равновесной, но при специальном выборе сдвигов b’ и b» обладает относительным минимумом энергии (по сравнению с укладками при других значениях b’ и b», удовлетворяющих условию b’+b»=b). Такие поверхностные дефекты называются дефектами упаковки. Пример дефекта упаковки приводился в § 2. Обозначим у-удельную поверхностную энергию дефекта упаковки. Теперь можно записать условие расщепления дислокации в кристалле в виде

Здесь U(l)—энергия упругого взаимодействия параллельных дислокации b’ и b», находящихся на расстоянии l. Если векторы b, b’, b» не параллельны, то множители при их квадратах другие [см. (17.9)].

В качестве примера образования дефекта упаковки рассмотрим сдвиг в плоскости в ГЦК-решетке.

44. Образование краевой дислокации с вектором Бюргерса b в ГЦК-решетке путем внедрения полуплоскости РР’ (проекция на плоскость (111):

Как атомные слои расположены (снизу вверх) в порядке АВС. Атомы слоя В и всех вышележащих слоев ‘раздвигаются в направлении вектора b и ему противоположном и в образовавшуюся (не плоскую) щель вставляется дополнительный слой атомов указано в гл. 1, эту решетку можно представить в виде плотной упаковки шаров с порядком чередования слоев . АВСАВС. Если шары каждого третьего слоя распо-лагаются над шарами первого, то наблюдается порядок укладки . АВАВА. типичный для гексагональной ре шетки.

Введем в представленный на рис. 44 участок ГЦК-кристалла краевую дислокацию с вектором Бюргерса b, экстраплоскость которой располагается выше плоскости рисунка и обрывается вдоль прямой PP/ на уровне атом ного слоями. При этом как атомы, экстраплоскости, так и соседние раздвинутые атомы исходной решетки оказы-ваются не в лунках слоя Л, как нормальные атомы слоя 5, а упираются в боковую поверхность шаров, например шара A’, Разумеется, атомы—не твердые шары и приведенные рассуждения лишь показывают, что характерное для ГЦК-решетки взаимное расположение соседних атомов при сдвиге атомов слоя В в направлении b нарушается и такой сдвиг приводит к энергетически невыгодным конфигурациям. Выгоднее будет атомам края экстраплоскости (и соседним) сместиться еще и по нормали к b и попасть в лунки С, находясь в которых атомы имеют правильное число ближайших соседей. В резуль-

45, Атомная структура расщепленной дислокации в ГЦК-решетке меди:

результаты расчета на ЭВМ положений атомов в двух плоскостях . одна из которых выше (треугольники), а другая ниже (кружки) плоскости скольжения. Положение линии первоначальной нерасщепленной дислокации вдоль направления указано средней стрелкой. Частичные дислокации, указанные боковыми стрелками, и область дефекта упаковки между ними хорошо видны, если рассматривать рисунок под малым углом сбоку

тате установится порядок чередования атомных позиций вдоль нормали к плоскости скольжения (снизу вверх) . ABCA! CABC. (чертой отмечено место обрыва экстраплоскости). Но в этом случае можно в пространстве разделить сдвиги ВС и СВ’, расщепив дислокацию с вектором Бюргерса b на две частичные с неколлинеарными векторами Бюргерса b’ и b», между которыми располагается полоска дефекта упаковки (рис. 45). В данном случае длина векторов b’ и b» равна а/ ]/6.

Векторы Бюргерса полных и частичных дислокации принято выражать через их проекции на ребра элементарной ячейки кристаллической решетки. В ГЦК-решетке векторы Бюргерса полной и частичной дислокации-записываются соответственно в виде b==1/2a , b’= =1/2a . Иногда множитель а опускается.

Нетрудно найти равновесную ширину I дефекта упаковки (величину расщепления дислокации). Она определяется из равенства сил отталкивания f частичных дисло каций силе поверхностного натяжения у дефекта упаковки. Приняв во внимание направления векторов b’ и b», получим

Энергия дефекта упаковки у является одной из фундаментальных характеристик кристалла. Она колеблется в пределах от десятков до сотен миллиджоулей на квадратный метр (см. табл. 2). Расщепление изменяется соответственно в пределах от долей до десятков нанометров. Уточним теперь правило построения контура Бюргерса в случае частичной дислокации. В отличие от полной, дислокации, когда начальный узел Л контура (см. рис. 18) выбирался в «хорошей» области кристалла произвольно, в случае частичной дислокации он должен ле-

46. Построение контура Бюргерса для расщепленной дислока — дни и составляющих ее частичных дислокации: контурм построены в (искривленной) плоскости Р

жать в плоскости дефекта упаковки, обрывающегося на частичной дислокации, точнее, в каком-либо узле одной| из двух атомных плоскостей, между которыми лежит дефект упаковки. В качестве примера на рис. 46 представ лен участок М2М3М5М6 плоскости Р, который гресекает расщепленная краевая дислокация. Поскольку векторы Бюргерса b’ и b частичных дислокации имеют винтовой компонент, рассматриваемый участок плоскости Р искривлен (см. рис. 21). Одна частичная дисло’ кация расположена между точками О и R, другая — между 5 и Q. Между ними лежит полоска дефекта упаковки. Если атомы левее О и правее Q лежат в лунках типа В, то атомы N, S и лежащие в одном ряду с ними находятся в лунках типа С, Начиная построение контура Бюргерса для левой частичной дислокации, выберем в плоскости дефекта — упаковки (точнее, в прилегающей к ней сверху атомной плоскости) узел М (заметим, что в этом узле атома нет: до образования дефекта упаковки в нем находился атом, который теперь занимает узел N). Двигаясь вдоль контура Бюргерса, совершаем один шаг в направлении ММ1 четыре шага влево в направлении M1М2, три шага М2М3 в направлении, противоположном MM1 четыре шага вправо М3М4 и недостающие до завершения обхода два шага M4N. Невязка контура NM есть вектор Бюргерса Ь’ частичной дислокации, лежащий в плоскости ее скольжения. Чтобы обойти правую частичную дислокацию, начиная обход в плоскости дефекта упаковки, выберем за начало обхода точку N и проведем контур. Бюргерса в той же искривленной плоскости Р: NM4M5M6M7R. Невязка RN=b». Обход по контуру М1М2М3М5М6М7, охватывающему обе частичные. дислокации, дает, разумеется, невязку M7M1 равную вектору b=b’+b» решетки.

Рассмотренные выше частичные дислокации имеют вектор Бюргерса, лежащий в плоскости скольжения. Такие скользящие частичные дислокации называются дu-слокациями Шокли. Возможны частичные дислокации, вектор Бюргерса которых не лежит в плоскости скольжения. Такие сидячие дислокации называются дислока циями Франка. Их простейшим примером является край экстраплоскости , вставленной между плоскостями в ГЦК-кристалле (см. рис. 5, б). Если экстраплоскость расположена между плоскостями Л и В, ее атомы могут находиться только в узлах С (соседние плоскости типов АА, ВВ, СС нарушают энергетически выгодную плотную упаковку шаров). Дислокация Франка ограничивает в этом случае дефект упаковки внедрения . ABCACBCABC. а ее вектор Бюргерса равен 1/3a . Если из нормального чередования изъять одну плоскость, например В, то получится дефект упаковки вычитания . АВСАСАВС. . Он. может быть ограничен также частичной дислокацией Франка, однако, как показано выше, он может быть получен также сдвигом на вектор b’=1/6а и, следовательно, обрываться на такой же дислокации b’. Дефекты упаковки вычитания называются также собственными дефектами упаковки (англ. intrinsic) в отличие от несобственных дефектов упаковки внедрения (англ. extrinsic).

Как мы уже видели, дефекты упаковки вычитания и внедрения ограниченных размеров образуются в результате коалесценции (объединения) избыточных вакансий и межузельных атомов соответственно.

Другим примером частичных дислокации являются рассмотренные в § 8 вершинные дислокации (англ. stair rod dislocation), образующие ребра тетраэдров дефектов упаковки. Их векторы Бюргерса равны 1/6a .

Видео:Угол между векторами. 9 класс.Скачать

15. термопара

15.1. ГЛАВА IX

ТЕРМОЭЛЕКТРИЧЕСКИЕ И ГАЛЬВАНОМАГНИТНЫЕ ЯВЛЕНИЯ

К термоэлектрическим явлениям относятся эффекты Зеебека, Пель-тье и Томсона, к гальваномагнитным—эффекты Холла, Эттинсгаузе-на и Нернста. Ряд из этих явлений нашли широкое применение, поэтому ознакомление с ними имеет не только познавательный, но и практический интерес.

Рассмотрим кратко физическую сущность этих явлений.

15.2. § 79. ЭФФЕКТ ЗЕЕБЕКА.

В 1823 г. Т. Зеебек установил, что в цепи, состоящей из двух разнородных проводников / и 2, возникает электродвижущая сила Vr, если контакты этих проводников Лий поддерживаются при различных температурах T1 и T2 (рис. 9.1, а). Эта э. д. с. называется термоэлектродвижущей силой (тер МО-э, д. с.). Как показывает опыт, в относительно узком интервале температур она пропорциональна разности температур контактов А и В:

(9.1)

называют дифференциальной или удельной термо-э. д. с. Он зависит от природы соприкасающихся проводников и температуры.

Существует три источника возникновения термо-э. д. с.: образование направленного потока носителей в проводнике при наличии градиента температур (объемная составляющая Vоб), изменение положения уровня Ферми с температурой (контактная составляющая У к) и увлечение электронов фононами.