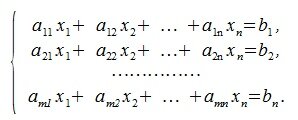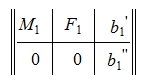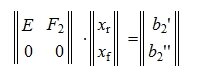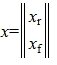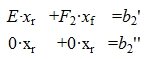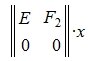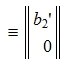Общее решение неоднородной системы уравнений АХ = В равняется сумме частного решения этой системы К и линейной комбинации решений фундаментальной системы решений соответствующей однородной системы уравнений АХ = 0, т.е.
где К — какое-либо решение неоднородной системы уравнений АХ= В:
FvF2, . Fk — фундаментальная система решений однородной системы уравнений АХ = 0;
1. Подставим X = К + F1tl + F2t2+ . + Fktk в уравнение АХ = В, получим
так как векторы Fv /у, . /у являются решениями однородной системы АХ = 0.
Следовательно, X является решением системы АХ = В.
2. Покажем, что любое решение уравнения АХ = В имеет вид
Пусть К — некоторое частное решение уравнения АХ = B,L — любое другое решение этого же уравнения. Разность этих решений (L — К) является решением однородного уравнения АХ = 0. Действительно, A(L — К) = AL — АК = В — В = 0. Поэтому L — К является линейной комбинацией векторов-решений фундаментальной системы однородной системы уравнений, т.е.
Отсюда
Пример 4.2. Найти и записать в векторном виде общее решение системы уравнений
Решение. Приводим исходную систему уравнений к равносильной разрешенной системе уравнений. Последовательность вычислений приведена в таблице.
В результате получаем
В качестве частного решения этой системы уравнений можно взять ее базисное решение. Полагаем х3 = х4 = х5 = 0, получаем х = 2,
Найдем фундаментальную систему решений соответствующей однородной системы уравнений
Находим три линейно независимых частных решения этой системы. Задавая свободным неизвестным значения х3 = 1, х4 = 0, х5 = О, находим х = 4, х2 = 1. Имеем частное решение /у = (-4, 1, 1, 0, 0). Задавая свободным неизвестным значения х., = 0, х4 = 1, х = 0, находим значения х = -4, х2 = -3. Имеем частное решение F2 = (-4, -3, 0, 1, 0). Задавая свободным неизвестным значения х., = 0, х4 = 0, х = 1 находим х< = -5, х2 = -1. Имеем частное решение F3 = (-5, -1, 0, 0, 1). Данные вычисления удобно записать в виде таблицы.
- Лекции по высшей математике, линейная алгебра (стр. 4 )
- 2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.
- 3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
- Система линейных уравнений. Общее решение
- Нахождение общего решения системы линейных уравнений
- Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы
- 📺 Видео
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Лекции по высшей математике, линейная алгебра (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Запишем в разных видах систему уравнений 



x 1 


Вектор`x * = 
Система уравнений называется совместной, если она имеет хотя бы одно решение.
Система уравнений называется несовместной, если она не имеет ни одного решения.
Система уравнений называется определенной, если она имеет ровно одно решение.
Система уравнений называется неопределенной, если она имеет более одного решения.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

2. СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ.
Квадратная матрица A называется невырожденной, если ее строки линейно независимы.
Согласно этому определению, свойствам определителей, критерию существования обратной матрицы получаем, что невырожденная матрица имеет ненулевой определитель и обладает обратной матрицей.
Благодаря этим свойствам имеем два особых метода решения системы A`x =`b с квадратной невырожденной матрицей A.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СЛУ.
Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * этой системы, равное произведению обратной матрицы A– 1 на столбец свободных членов`b, `x * = A– 1`b.
Докажем сначала, что вектор`x * является решением системы A`x =`b. В самом деле, A`x * = A · A– 1`b = E`b =`b, то есть A`x * =`b и`x * является решением системы A`x =`b.
Докажем теперь единственность этого решения. Предположим, что имеется еще другое решение`x 1, то есть A`x 1 =`b — верное равенство. Домножим обе части этого равенства слева на A– 1. Получим A– 1 A`x 1 = A– 1`b и, следовательно,`x 1 = A– 1`b, то есть`x 1 =`x *. Теорема доказана.
Таким образом, матричный метод решения системы A`x =`b с квадратной невырожденной матрицей A состоит в нахождении решения этой системы по формуле`x * = A– 1`b.
Если матрица A системы A`x =`b квадратная невырожденная, то существует единственное решение`x * = 



ПРИМЕР решения системы линейных уравнений по правилу Крамера.

D = 





Видео:ФСР системы линейных уравнений. Алгоритм ГауссаСкачать

3. ОБЩИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.
Рассмотрим систему уравнений A`x =`b с произвольной матрицей A. Исследуем вопрос о ее совместности и количестве решений.
ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ.
Для того, чтобы система уравнений A`x =`b была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы равнялся рангу ее расширенной матрицы.
1) Пусть система уравнений A`x =`b является совместной. Докажем, что ранг r A матрицы A равняется рангу r à расширенной матрицы Ã.
Представим матрицы A и Ã как системы их векторов столбцов
соответственно. Ранг матрицы A равен рангу системы векторов (1), а ранг матрицы Ã равен рангу системы векторов (2). Поскольку система векторов (1) является подсистемой системы векторов (2), то r A £ r Ã.
Так как система A`x =`b является совместной, то существует вектор `x * = 
`A 1,`A 2 , … ,`A n ,`b Î L (`A 1,`A 2 , … ,`A n ). По свойствам ранга системы векторов r à £ r A. Но так как r A £ r à , то r A = r à .
2) Пусть теперь r A = r à = r. Докажем, что система A`x =`b является совместной. Согласно определению базиса системы векторов базисы систем (1) и (2) содержат по r векторов. Пусть`A 1, `A 2 , … ,`A r — базис системы (1). Тогда эти же векторы будут являться и базисом системы (2). Действительно, векторы`A 1,`A 2 , … ,`A r образуют линейно независимую подсистему системы (2), а поскольку их количество совпадает с рангом системы (2), то они являются базисом этой системы. Следовательно, вектор`b можно представить в виде линейной комбинации векторов`A 1,`A 2 , …,`A r :
`b = l 1`A 1 + l 2`A 2 + … + l r`A r, а также в виде линейной комбинации
`b = l 1`A 1 + l 2`A 2 + … + l r`A r + 0`A r + 1 + … + 0`A n. Справедливость последнего равенства означает, что вектор`x *, координатами которого являются числа l 1, l 2 , … , l r , 0, … , 0 является решением системы уравнений A`x =`b, то есть система A`x =`b совместна. Теорема доказана.
ТЕОРЕМА ОБ ОПРЕДЕЛЕННОСТИ СЛУ.
Пусть система уравнений A`x =`b является совместной, имеет n неизвестных и r A = r à = r.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Система линейных уравнений. Общее решение
Система линейных уравнений (СЛУ) может быть записана в виде
где m, n натуральные числа, aij (i= 1,2, . m, j= 1,2. n) называются коэффициентами, bi (i= 1,2. m) называются свободными членами, xi (i= 1,2. n) называются неизвестными.
Систему линейных уравнений (1) можно записать в виде
где A матрица порядка m×n , x — вектор порядка n (x∈R n ), b — вектор порядка m (b ∈R m ).
Решением системы (2) называется выбор такого вектора x’, что выполнено равенство
Если система линейных уравнений имеет хотя бы одно решение, то СЛУ называется совместным.
Если СЛУ не имеет решения, то СЛУ называется несовместным.
Если СЛУ имеет единственное решение, то СЛУ называется определенным.
Если СЛУ имеет более одного решения, то СЛУ называется неопределенным.
Система линейных уравнений (2) называется неоднородной cистемой линейных уравнений, если b≠0.
Система линейных уравнений (2) называется однородной cистемой линейных уравнений, если b=0.
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Нахождение общего решения системы линейных уравнений
Общее решение системы линейных уравнений (1)((или (2))− это множество всех решений этой системы.
Пусть A m×n — матрица rankA=r. В общем случае можем предположить что r 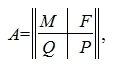
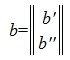
Применяя метод исключения Гаусса для системы (3), получим:
где M1 верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:
где E — единичная матрица порядка r×r.
Запишем (5) в виде системы линейных уравнений:
где
Решим систему линейных уравнений (6). Для этого перезапишем в следующем виде:
Из второго уравнения системы (7) следует, что для совместности системы (6) и, следовательно, (2) (или (1)) должно выполняться условие b2»≡ 0. Если система совместна, то решаем первое уравнение системы (7) относительно вектора xr:
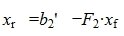 | (8) |
Таким образом первые r координаты вектора x 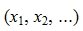
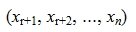
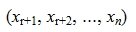
Найдем, далее, множество всех векторов x, удовлетворяющих уравнению (6) и, следовательно, (2)( или (1)).
Рассмотрим множество всех векторов х, удовлетворяющих условию
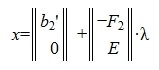 | (9) |
где λ — произвольный вектор-столбец длины n-r.
Подставляя (9) в (6) получим:
Следовательно (9) является решением системы (6) и, следовательно, (2)(или (1)). Отметим что вектор 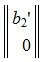
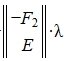
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы
Обозначим через R(A) пространство столбцов матрицы A, т.е.
1. Пусть A n×n матрица и rank(A)=n. Тогда существует обратная к A матрица A -1 , и следовательно единственное решение СЛУ (2) примет вид:
Действительно, подставляя (3) в (2) имеем:
2. Пусть A m×n − матрица, rank(A)=r.
📺 Видео
Решение системы уравнений методом ГауссаСкачать

Графический и векторный способ решения систем линейных уравнений.Скачать

Базисные решения систем линейных уравнений (03)Скачать

Фундаментальная система решений системы линейных уравнений ФСР СЛАУСкачать

Видеоурок "Однородные системы линейных уравнений"Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

Решение систем линейных уравнений с помощью матрицСкачать

10. Метод Крамера решения систем линейных уравнений.Скачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Матричный метод решения систем уравненийСкачать