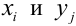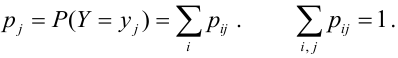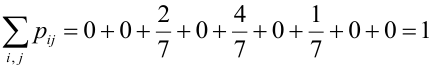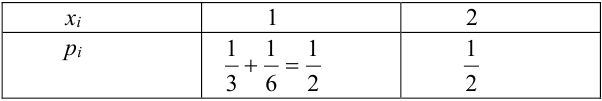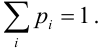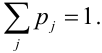Ранее мы разобрали примеры решений задач для одномерной дискретной случайной величины. Но бывает, что результат испытания описывается не одной, а несколькими случайными величинами (случайным вектором).
В случае двух величин (скажем, $X$ и $Y$) мы имеем дело с так называемой двумерной дискретной случайной величиной $(X,Y)$ (или системой случайных одномерных величин). Кратко выпишем основы теории.
Видео:Двумерное дискретное распределениеСкачать
Система двух случайных величин: теория
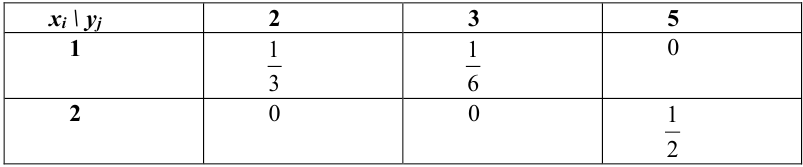
Двумерная ДСВ задается законом распределения (обычно представленным в виде таблицы распределения):
$$ P(X=x_i, Y=y_k)=p_, i=1,2. m; k=1,2. n; quad sum_p_=1. $$
По нему можно найти одномерные законы распределения (составляющих):
$$ p_i=P(X=x_i)=sum_p_, i=1,2. m; \ p_k=P(Y=y_k)=sum_ p_, k=1,2. n. $$
Интегральная функция распределения задается формулой $F(x,y)=P(Xlt x, Ylt y)$. Даже для самого простого закона распределения 2 на 2 функция занимает 5 строк, поэтому ее редко выписывают в явном виде.
Если для любой пары возможных значений $(X=x_i, Y=y_k)$ выполняется равенство
$$P(X=x_i, Y=y_k)=P(X=x_i)cdot P(Y=y_k),$$
то случайные величины $X, Y$ называются независимыми.
Если случайные величины зависимы, для них можно выписать условные законы распределения (для независимых они совпадают с безусловными законами):
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
Далее вы найдете разные примеры задач с полным решением, где используются дискретные двумерные случайные величины (системы случайных величин).
Видео:Теория вероятностей #18: системы двух случайных величин, двумерное распределениеСкачать
Примеры решений
Задача 1. В продукции завода брак вследствие дефекта А составляет 10%, а вследствие дефекта В — 20%. Годная продукция составляет 75%. Пусть X — индикатор дефекта А, a Y — индикатор дефекта В. Составить матрицу распределения двумерной случайной величины (X, Y). Найти одномерные ряды распределений составляющих X и У и исследовать их зависимость.
Задача 2. Два баскетболиста по два раза бросают мяч в корзину. При каждом броске вероятность попадания для первого баскетболиста 0,6, для второго – 0,7. Случайная величина X – число попаданий первым баскетболистом по кольцу. Случайная величина Y – суммарное число попаданий обоими баскетболистами. Построить таблицу распределения случайного вектора (X,Y). Найти характеристики вектора (X,Y). Зависимы или независимы случайные величины X и Y.
Задача 3. Слово РОССИЯ разрезано по буквам. Случайным образом вынимаем две буквы, тогда X – количество гласных среди них, затем вынимаем еще две буквы и Y – количество гласных во второй паре. Составить закон распределения системы случайных величин X, Y.
Задача 4. $X, Y$ — индикаторы событий $A, B$, означающий положительные ответы соответственно на вопросы $alpha, beta$ социологической анкеты. По данным социологического опроса двумерная случайная величина $(X,Y)$ имеет следующую таблицу распределения.
Положительному ответу присвоен ранг 1, отрицательному – 0.
Найти коэффициент корреляции $rho_$.
Задача 5. Составить закон распределения X — сумм очков и Y — числа тузов при выборе двух карт из колоды, содержащей только тузов, королей и дам (туз=11, дама=3, король=4)
Найти законы распределения величин Х и Y. Зависимы ли эти величины? Написать функцию распределения для (Х, Y). Построить ковариационный граф. Посчитать ковариацию (X,Y). Написать ковариационную матрицу. Посчитать корреляцию (X,Y) и написать корреляционную матрицу.
Задача 6. Бросаются две одинаковые игральные кости. Случайная величина X равна 1, если сумма выпавших чисел четна, и равна 0 в противном случае. Случайная величина Y равна 1, если произведение выпавших чисел четно, и 0 в противном случае. Описать закон распределения случайного вектора (X,Y). Найти D[X], D[Y] и cov[X,Y].
Задача 7. В урне лежат 100 шаров, из них 25 белых. Из урны последовательно вынимают два шара. Пусть $X_i$ – число белых шаров, появившихся при $i$-м вынимании. Найти коэффициент корреляции между величинами $X_1$ и $X_2$.
Задача 8. Для заданного закона распределения вероятностей двухмерной случайной величины (Х, Y):
YX 2 5
8 0,15 0,10
10 0,22 0,23
12 0,10 0,20
Найти коэффициент корреляции между величинами Х и Y.
Задача 9. Задана дискретная двумерная случайная величина (X,Y).
А) найти безусловные законы распределения составляющих;
Б) построить регрессию случайной величины Y на X;
В) построить регрессию случайной величины X на Y;
Г) найти коэффициент ковариации;
Д) найти коэффициент корреляции.
20 30 40 50 70
3 0,01 0,01 0,02 0,02 0,01
4 0,04 0,3 0,06 0,03 0,01
5 0,02 0,03 0,06 0,07 0,05
9 0,05 0,03 0,04 0,02 0,03
10 0,03 0,02 0,01 0,01 0,02
Задача 10. Система (x, y) задана следующей двумерной таблицей распределения вероятностей. Определить:
А) безусловные законы распределения составляющих;
Б) условный закон распределения y при x=1;
В) условное математическое ожидание x при y=2.
Г) вероятность того, что случайная величина (x,y) будет принадлежать области $|x|+|y|le 3$.
-3 0 2
-1 0 0,1 0,15
1 0,05 0,3 0,05
2 0,15 0,05 0,15
Видео:Случайный вектор двумерной случайной величиныСкачать
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Видео:Функция распределения дискретной случайной величиныСкачать
Системы случайных величин — определение и вычисление с примерами решения
Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) — двумерный случайный вектор или система двух СВ.
Изучать систему — значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Видео:Корреляция и ковариация двумерной случайной величиныСкачать
Законы распределения СВДТ и СВНТ
Таблица распределения — закон распределения СВДТ:
Рассмотрим двумерный случайный вектор (X, У), где X и У — дискретные случайные величины с возможными значениями 
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х — число четных цифр в выборке, Y — число нечетных. Описать закон распределения.
Решение.
X (четные) — 2, 4, 6, 8; Y ( нечетные) — 1, 3, 9. Следовательно, возможные значения X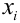 
: 
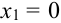
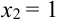
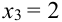
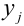
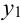
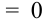
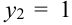
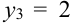
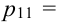
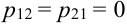
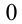
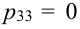
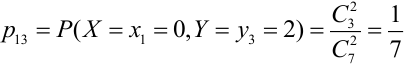
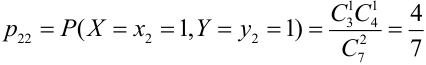
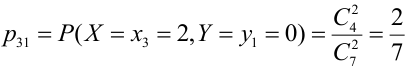
(нет четных цифр), 
(одна цифра четная), 
(обе цифры четные); возможные значения Y 
: 
(нет нечетных цифр), 
(одна цифра нечетная), 
(обе цифры нечетные). Найдем вероятности.
(0 четных, 0 нечетных) = 0, не выбираем ни одной цифры, а по условию выбираем две цифры. Аналогично, 
(выбираем всего одну цифру либо нечетную, либо четную), 
(выбираем три цифры вместо двух по условию), 
(выбираем четыре цифры вместо двух по условию).
— (обе цифры нечетные),
— (одна четная, одна нечетная),
— (обе цифры четные).
Таблица распределения имеет вид:
Проверка: 
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
Решение.
, (складываем по строкам), следовательно,
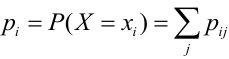
Проверка: 
, (складываем по столбцам), следовательно,
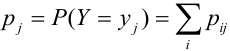
Проверка: 
Функция распределения — закон распределения СВДТ и СВНТ
Функция распределения — универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Теория вероятностей #12: случайная величина, плотность и функция распределенияСкачать
Дискретный двумерный случайный вектор
В этом разделе рассмотрены числовые характеристики только двумерных случайных величин, поскольку обобщение на случай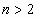 
не вызывает затруднений.
Пусть ( x , h ) — двумерная случайная величина, тогда M( x , h )=(M( x ), M( h )), т.е. математическое ожидание случайного вектора — это вектор из математических ожиданий компонент вектора.
Если ( x , h ) — дискретный случайный вектор с распределением
| y1 | y2 | . | ym | |
| x1 | p11 | p12 | . | p1m |
| x2 | p12 | p12 | . | p2m |
| . | . | . | pij | . |
| xn | pn1 | pn2 | . | pnm |
то математические ожидания компонент вычисляются по формулам:
, 
.
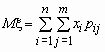
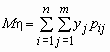
Эти формулы можно записать в сокращенном виде.
Обозначим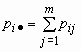 
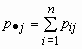
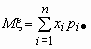
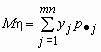
и 
, тогда 
и 
.
Если p( x , h )(x, y)- совместная плотность распределения непрерывной двумерной случайной величины ( x , h ), то
и 
.
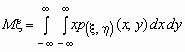
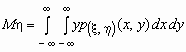
Поскольку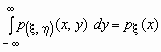 
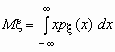
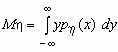
-плотность распределения случайной величины x , то 
и, аналогично, 
.
Понятие дисперсии обобщается на многомерные случайные величины нетривиальным образом. Это обобщение будет сделано в следующем разделе. Здесь лишь приведем формулы для вычисления дисперсии компонент двумерного случайного вектора.
Если ( x , h ) — двумерная случайная величина, то
D x = M( x — M x ) 2 = M x 2 — M( x ) 2 , D h = M( h — M h ) 2 = M h 2 — M( h ) 2 .
Входящие в эту формулу математические ожидания вычисляются по приведенным выше формулам.
Между случайными величинами может существовать функциональная зависимость. Например, если x — случайная величина и h = x 2 , то h — тоже случайная величина, связанная с x функциональной зависимостью. В то же время между случайными величинами может существовать зависимость другого рода, называемая стохастической. В разделе, посвященном условным распределениям уже обсуждалась такая зависимость. Из рассмотренных там примеров видно, что информация о значении одной случайной величины (одной компоненты случайного вектора) изменяет распределение другой случайной величины (другой компоненты случайного вектора), а это может, вообще говоря, изменить и числовые характеристики случайных величин.
Математическое ожидание, вычисленное по условному распределению, называется условным математическим ожиданием.
Для двумерного дискретного случайного вектора ( x , h ) с распределением
| y1 | y2 | . | ym | |
| x1 | p11 | p12 | . | p1m |
| x2 | p12 | p12 | . | p2m |
| . | . | . | pij | . |
| xn | pn1 | pn2 | . | pnm |
условное математическое ожидание случайной величины x при условии, что случайная величина h принимает значение yj, вычисляется по формуле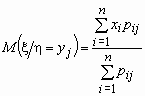 
.
Аналогично, условное математическое ожидание случайной величины h при условии, что случайная величина x принимает значение xi, равно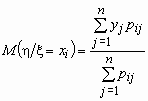 
.
Видно, что условное математическое ожидание случайной величины x является функцией значений случайной величины h , т.е. M( x / h = y) = f1(y) и, совершенно аналогично, M( h / x = x) = f2(x).
Функцию f1(y) называют регрессией случайной величины x на случайную величину h , а f2(x) — регрессией случайной величины h на случайную величину x .
Если p( x , h )(x, y) совместная плотность вероятностей двумерной случайной величины ( x , h ), то
и 
.
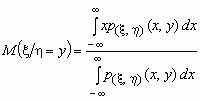
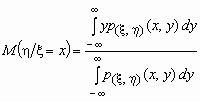
Если между случайными величинами x и h существует стохастическая связь, то одним из параметров, характеризующих меру этой связи является ковариация cov( x , h ). Ковариацию вычисляют по формулам cov( x , h )=M[( x — M x )( h — M h )] = M( x h ) — M x M h .
Если случайные величины x и h независимы, то cov( x , h )=0.
Обратное, вообще говоря, неверно. Из равенства нулю ковариации не следует независимость случайных величин. Случайные величины могут быть зависимыми в то время как их ковариация нулевая! Но зато, если ковариация случайных величин отлична от нуля, то между ними существует стохастическая связь, мерой которой и является величина ковариации.
cov( x , x ) = D x ;
;
;
,
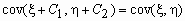
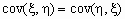
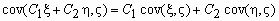
Ковариационной матрицей случайного вектора ( x , h ) называется матрица вида
.
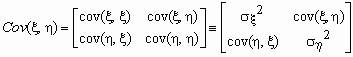
Эта матрица симметрична и положительно определена. Ее определитель называется обобщенной дисперсией и может служить мерой рассеяния системы случайных величин ( x , h ).
Как уже отмечалось ранее, дисперсия суммы независимых случайных величин равна сумме их дисперсий: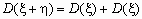 
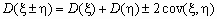
. Если же случайные величины зависимы, то 
.
Понятно, что значение ковариации зависит не только от “тесноты” связи случайных величин, но и от самих значений этих величин, например, от единиц измерения этих значений. Для исключения этой зависимости вместо ковариации используется безразмерный коэффициент корреляции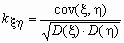 
.
Этот коэффициент обладает следующими свойствами:
его модуль не превосходит единицы, т.е.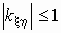 
;
если x и h независимы, то k( x , h )=0 (обратное неверно!);
если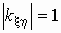 
, то случайные величины x и h связаны функциональной зависимостью вида
где a и b- некоторые числовые коэффициенты;
;
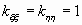
Корреляционной матрицей случайного вектора называется матрица
.
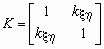
Если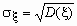 
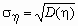
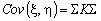
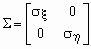
и 
, то ковариационная и корреляционная матрицы случайного вектора ( x , h ) связаны соотношением 
, где 
.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
💥 Видео
Математика без Ху!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.Скачать
Двумерные дискретные случайные величины. ТемаСкачать
Условные и безусловные распределенияСкачать
Дискретная двумерная случайная величина. Закон распределенияСкачать
Зависимость компонент двумерного распределенияСкачать
Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать
Функция распределения непрерывной случайной величины. Вероятность попадания в интервалСкачать
02-05 Многомерное нормальное распределениеСкачать
Дискретная случайная величина и ее свойстваСкачать
Закон распределения дискретной случайной величиныСкачать
2.8. Совместное распределение двух случайных величин.Скачать
Функция распределения и плотность распределенияСкачать
12. ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕКТОРЫ 📚 Теория вероятностейСкачать
Дискретный случайный вектор и его характеристикиСкачать
