Конспект вписанная и описанная окружности 8 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

УРОКИ-КОНСПЕКТЫ ПО ГЕОМЕТРИИ 8 КЛАСС

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ

Цели: ввести понятие вписанной окружности и описанного около окружности многоугольника; рассмотреть теорему о том, что в любой треугольник можно вписать окружность.

I. Проверка домашнего задания.

1) а) Докажите, что АВМ = МСА.

б) АМ = 4, МD = 3, ВD = 4.

Найдите расстояние от точки М до стороны АС.

2) Найдите МKN и расстояние MN, если ОМ = , KМ = 3.

3) Найдите углы АВС, если ОАС = 20° и АОС = 120°.

4) стороны угла А касаются окружности радиуса r с центром О.

а) Найдите ОА, если r = 5 см, А = 60°.

б) Найдите r, если ОА = 14 дм, А = 90°.

II. Изучение нового материала.

Изложить в виде лекции п. 74 до замечания 2.

III. Закрепление изученного материала.

Выполнить №№ 701 (для остроугольного треугольника), 689, 691.

1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как СМ АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r.

Далее обсудить с учащимися различные способы решения этой задачи:

1. АМ = AB = 5 см.

2. M и N – точки касания, следовательно, AN = АМ = 5 см, откуда CN = АС – АN = 8 cм.

3. В АСМ : СМ = = 12 (см).

4. В СON : СО2 = СN2 + ON2, то есть (12 – r )2 = 82 + r 2

144 – 24r + r2 = 64 + r2.

r = 3 .

ОМ = ON = 3 см .

1. В АСМ : АМ = AB = 5 см.

СМ = = 12 (см).

2. Отрезок АО – биссектриса треугольника АМС (так как О – центр вписанной окружности), поэтому или ; 13r = 60 – 5r, r = 3.

ОМ = ОN = 3 см.

1) Центр вписанной в треугольник окружности в точке пересечения биссектрис;

2) ОМ = ON = ОK – радиусы вписанной окружности;

3) окружность единственная для данного треугольника.

Домашнее задание: вопросы 21, 22, с. 188; №№ 701 (для прямоугольного и тупоугольного треугольников), 637, 690, 693 (а), 693 (б) – по желанию и используя № 697 III способ решения № 698.

1) О – центр вписанной окружности в треугольник АВС, который лежит на высоте (биссектрисе) равнобедренного треугольника, проведенной к основанию.

2) ОМ = ОD – радиусы этой окружности.

3) Пусть k – коэффициент пропорциональности, тогда ОВ = 12k см, ОD = ОМ = 5k см.

4) Прямоугольные треугольники ВDС и ВМО имеют общий угол В, и, значит, ВDС ВМО по первому признаку.

5) .

6) Из прямоугольного треугольника ВDС по теореме Пифагора имеем:DС = .

7) ; 5 = ;

625 = 3600 – 289k2

k2 = .

8) DC = = 25 (cм).

1) АС || ОN, так как АС СВ и ON CВ.

СВ || ОK, так как СВ АС и OK АС, значит, четырехугольник KONC – прямоугольник, а так как KО = CN = r = ON = KC, то KONC – квадрат.

2) АKО = АМО (по катету и гипотенузе), поэтому АK = АМ.

3) ВNO = ВМО (по катету и гипотенузе).

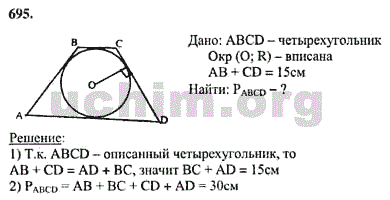
4) РАВС = АВ + ВС + АС = АМ + МВ + NB + CN + KC + АK.

РАВС = 2АМ + 2MВ + 2CN = 2(АМ + МВ + СN).

а) РАВС = 2(АВ + СN) = 2(26 + 4) = 60 (см).

б) Из АВС, С = 90° имеем по теореме Пифагора:

АС2 = АВ2 – СВ2 = АВ2 – (CN + NB) = 172 – (5 + r)2

ВС2 = АВ2 – АС2 = АВ2 – (АK + KС) = 172 – (12 + r)2

172 = 172 – (5 + r)2 + 172 – (12 + r)2

2r2 + 34r – 120 = 0

r = 3 (второй корень не удовлетворяет условию задачи).

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

Конспект урока по геометрии 8 класс на тему: «Решение задач на вписанную и описанную окружности»

Тип: урок рефлексии. Вид: комбинированный урок

Просмотр содержимого документа
«Конспект урока по геометрии 8 класс на тему: «Решение задач на вписанную и описанную окружности»»

Решение задач по теме: «Вписанная и описанная окружность»

1. Организационный момент.

Учитель: Я надеюсь, что следующие 45 минут нашего с вами взаимодействия будут комфортными и плодотворными. Для этого посмотрим, все ли готовы к уроку. На вашем рабочем месте вы увидите: опорный конспект, в котором вы будете работать на протяжении всего урока (положите его перед собой), учебник.

2. Мотивация учебной деятельности учащихся. Постановка цели и задач урока.

Сегодня мы с вами будет применять полученные знания на практике, а вот на какое геометрическое понятие, догадайтесь сами.

Учитель: Какое математическое понятие объединяет эти картинки.

Как вы, наверное, уже догадались, речь сегодня пойдёт о…окружности.

Учитель: Но не просто об окружности. О каких окружностях пойдёт речь? Слайд 3.

Учащиеся смотрят на экран и подбирают слова, которые ассоциируются у них с появившимся изображением. Это слова: ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ.

Учитель: Как вы сами сказали, тема урока…:

Решение задач по теме: «Вписанная и описанная окружность». Слайд 4.

(Запишите Ф.И. , тему урока в опросный конспект)

Цели. Определяют для себя в опорном конспекте. Слайд 5

Так как домашним заданием было повторить все понятия, теоремы и свойства которые связанны с вписанной и описанной окружностью, мы проведём самостоятельную работу. Она в ваших опорных конспектах. Вставьте нужные слова в определения или ответьте на вопрос (10 мин)

(Далее учащиеся меняются конспектами и с помощью учителя проверяют работу. Напротив правильного ответа ставим +, неправильного -)

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности. Слайд 6.

——-На каком рисунке окружность вписана в трапецию. (рис. 3)

Всегда ли можно вписать окружность в треугольник?Всегда

Всегда ли можно вписать окружность в четырехугольник? Не всегда

В выпуклый четырёхугольник можно вписать окружность только тогда, когда суммы противоположных сторон равны. Слайд 8.

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на данной окружности. Слайд 9А

Многоугольник называется вписанным в окружность, если все его вершины лежат на данной окружности. Слайд 10А

———Что лишнее? (фигуры синего цвета) Слайд 11

Где находится центр окружности, вписанной в треугольник? (Точка пересечения биссектрис) Слайд12

От чего равноудален центр описанной около треугольника окружности? (От вершин треугольника) Слайд 13А

Где находится центр окружности, описанной около треугольника? (Точка пересечения серединных перпендикуляров) Слайд 14А

В любой треугольник можно вписать окружность? (В любой)

Учитель: теперь подсчитайте количество + и запишите их количество, затем выставите оценку, ориентируясь на оценочной таблицей. Слайд 15.

Количество верных ответов_________ . Оценка ______

Если 10 верных ответов – оценка «5»

8-9 верных товетов — оценка «4»

6-7 верных ответов — оценка «3»

меньше 6 верных ответов – оценка «2»

Учитель: теперь приступим непосредственно к практике, а именно к решению задач.

Решение задач из учебника.

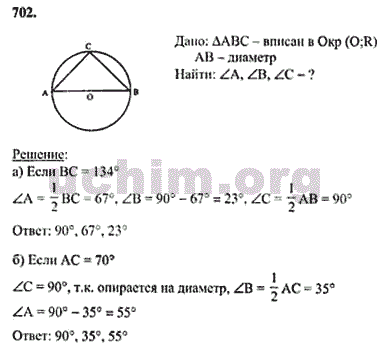
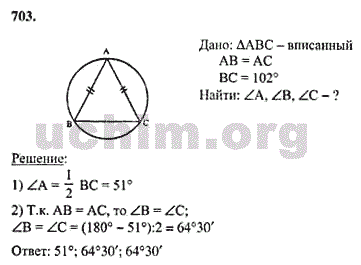
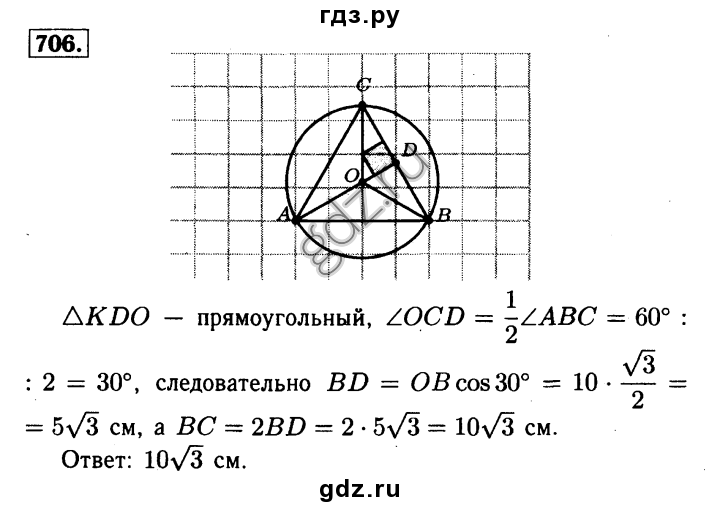
695, № 702 а Слайд 16. , 703 Слайд 17. (1 случай), Слайд 18. (2 случай), 706. Слайд 19.

Домашнее задание. Пар. 74, 75. № 702 б, 703 (другой случай), 705 б.

4 . Рефлексивно-оценочный этап.

Вернуться к целям.

Учитель: На стенах кабинета высказывания великих мыслителей.

1. «Как приятно знать, что ты что-то узнал!»

2. «Я знаю, что ничего не знаю»

3. «Скажи мне – и я забуду.

Покажи мне – и я запомню.

Вовлеки меня – и я научусь»

Ребят, подумайте, какая фраза больше всего отражает вашу деятельность на уроке. Пройдите к тому высказыванию, которое больше подходит к вам.

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Урок-практикум в 8-м классе «Вписанные и описанные окружности»

Разделы: Математика

Тип урока: урок — практикум.

Цели:

• систематизировать теоретический материал;
• совершенствовать навыки решения задач.

Учащиеся должны знать:

• свойства вписанной и описанной около треугольника окружности;
• свойства вписанной и описанной около четырехугольника окружности.

Учащиеся должны уметь:

• применять свойства для решения задач;
• формулировать свойства для решения задачи.

Обеспечение урока:

• учебник, тетрадь;
• мультимедиа проектор;
• карточки с заданием;
• письменные принадлежности.

🌟 Видео

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ВСЯ ГЕОМЕТРИЯ НА ОГЭ ЗА 3 ЧАСА | Математика ОГЭ 2023 | УмскулСкачать

Вписанная и описанная окружности. ЗадачиСкачать

ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

ВАЖНЫЕ УГЛЫ в Геометрии — Центральный и Вписанный УголСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Урок по теме ОПИСАННАЯ ОКРУЖНОСТЬ 8 классСкачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Геометрия 8 класс. Тема: "Вписанная и описанная окружности. Решение задач"Скачать