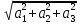Вектор равенство векторов координаты вектора (4 видео)

5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Видеоурок 1: Понятие вектора

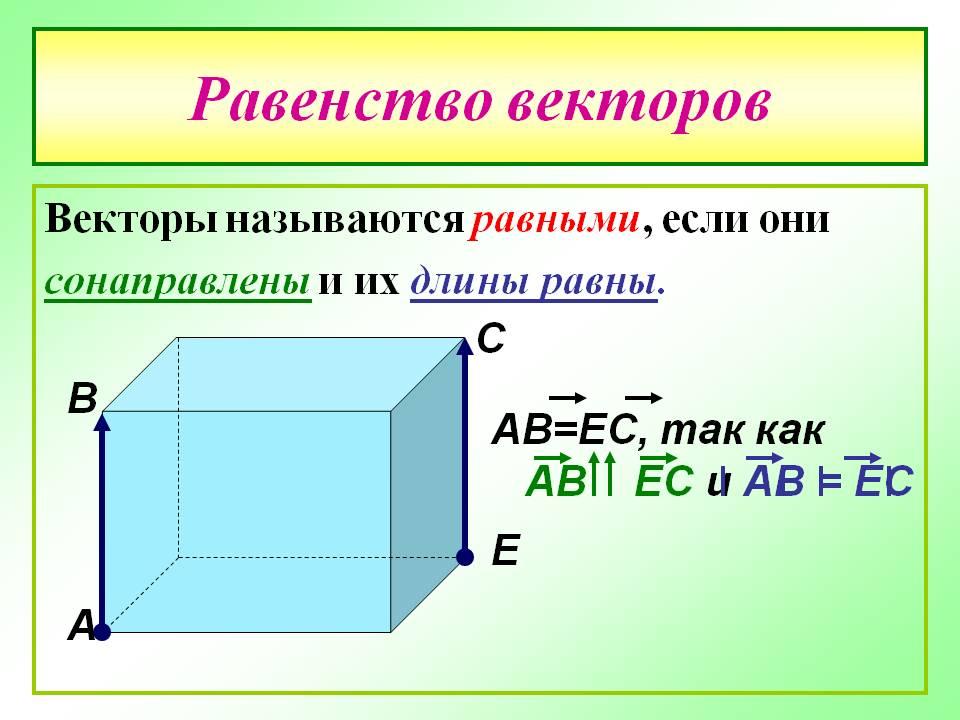
Видеоурок 2: Равенство векторов

Видеоурок 3: Сложение и вычитание векторов

Видеоурок 4: Умножение вектора на число

Лекция: Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Вектор

Вектор – это тело, которое изучается в математике, но используется в большом количестве наук. Например, в физике существуют скалярные величины (те, что характеризуются значением – масса, температура и т.д.), а также векторные величины (сила, работа и другие).

Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.

Но кроме его длины, нам также важно, где находится его начало, а где конец.

Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:

Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.

Длиной вектора (его модулем) называют расстояние между концом вектора и его началом.

Для определения модуля вектора следует воспользоваться следующей формулой:

Кроме этого, модуль вектора может обозначаться следующим образом:

Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как

Если длина некоторого вектора равна единичному отрезку, то его называют единичным.

Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными.

Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными.

Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными.

Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными.

Координаты вектора

Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала.

Например, если начало вектора А (3; 6), а конец В (5;9), то этот вектор будет иметь следующие координаты: .

Сложение и вычитание векторов

Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.

Например, сложим вектор с вектором . В результате получим новый вектор с координатами . С вычитанием все аналогично.

Умножение вектора на некоторое число

Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.

Первоначальный вектор и вектор умноженный на некоторое число, который равный ему, являются параллельными.
Если число, на которое умножался вектор, больше нуля, то новый вектор будет сонаправлен первоначальному. Если же число меньше нуля, то векторы будут противоположно направленны.

Содержание

«Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»
Просмотр содержимого документа ««Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»»
Вектор: определение и основные понятия
Определение вектора
Обозначение вектора
Длина вектора
Нулевой вектор
Коллинеарные вектора
Сонаправленные вектора
Противоположно направленные вектора
Компланарные вектора
Равные вектора
Единичный вектор
💥 Видео

Видео:Координаты вектора. 9 класс.Скачать

«Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»

Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.

Цели урока:

Образовательные:Изучить, что такое “вектор в пространстве», как определяются координаты, вектора, если известны координаты его начала и конца, научится решать задачи, связанные с векторами.

Развивающие: расширение кругозора учащихся, формирование умений применять приёмы сравнивания, обобщения, выделения главного, переноса знаний в новую ситуацию, развитие мышления, речи, умение комментировать, развитие учебно-познавательных компетенций учащихся

Воспитательные: воспитывать трудолюбие, чувство товарищества и взаимопомощи, привитие навыков самооценки, умения работать в коллективе, умения правильно оценивать работуодногруппников,прививать интерес к предмету.

План урока:

Организационный момент.
Актуализация знаний.
Изучение нового материала.
Закрепление знаний.
Итоги урока.
Самостоятельная подготовка.

Оборудование: Интерактивная доска

Тип урока: Комбинированный.

Ход урока:

1. Организационный момент.

Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.

2. Актуализация знаний

3. Изучение нового материала

ВЕКТОР. КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ

В пространстве, как и на плоскости, вектором называется величина, которая задается своей длиной и направлением. Вектор изображатеся направленным отрезком, длина которого равна длине вектора.

(Слайд 2)

Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.

Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты.

Определение. Координатами вектора , начало которого точка A(x1,y1,z1), а конец — точкаВ(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.

Записывают такой вектор, указывая его координаты: (a1 а2, а3) или (a1 а2, а3).

(Слайд 3)

Просмотр содержимого документа
««Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»»

Министерство образования, науки и молодежной политики Краснодарского края государственное бюджетное профессиональное образовательное учреждение Краснодарского края

«Лабинский социально-технический техникум»

«Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»

Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.

Изучение нового материала.

Оборудование: Интерактивная доска

Тип урока: Комбинированный.

1. Организационный момент.

2. Актуализация знаний

3. Изучение нового материала

ВЕКТОР. КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ

Определение. Координатами вектора , начало которого точка A(x₁,y₁,z₁), а конец — точкаВ(х₂, у₂, z₂), называются числа a₁= х_2- x_1,a₂=y₂-y_1, a₃=z₂-z₁.

Записывают такой вектор, указывая его координаты: (a₁ а₂, а₃) или (a₁ а₂, а₃).

Например, если точки А(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка , тогда

Значит, направленному отрезку соответствует вектор (-4; 6; 1) (рис. 67).

Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.

Длину вектора (a₁ а₂, а₃) можно выразить через его координаты. Отложим вектор от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а₁ и а₂, поэтому ОА_z 2 = а₁ 2 + а₂ 2 . В прямоугольном треугольнике ОА₂А второй катет А_z А = а₃ и ОА 2 = ОА 2 _г + а₃ 2 = а₁ 2 + а₂ 2 + а₃ 2 . Отсюда | | =

Длина любого ненулевого вектора — число положительное. Длина нулевого вектора равна нулю.

Вспомним, что два вектора, лежащих на одной прямой или параллельных прямых, называютколлинеарными. Коллинеарные векторы бывают сонаправлены (а b) или противоположно направлены (а b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.

ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ

Действия над векторами в пространстве осуществляются аналогично тому, как они определялись для векторов на плоскости.

Для любых векторов а , b и с справедливы равенства:

а+b=b+а — переместительный закон сложения;

а + (b + с) = (а+ b) + с — сочетательный закон сложения.

Чтобы доказать эти свойства, достаточно сравнить соответствующие

координаты левой и правой частей каждого векторного равенства.

Для любых трех точек А, В, С в пространстве имеет место векторное равенство + = .

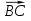
Действительно, для любых трех точек A(a₁ а₂, а₃), B(b₁ b₂, b₃), C(c₁, с₂, с₃) (b₁ – а₁; b₂ — а₂;b₃ — а₃) и (с₁ — b_г; с₂ — b₂, с₃ — b₃).

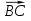
Отсюда + = (с₁ – а₁; с₂ — а₂; с₃ — а₃).

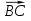
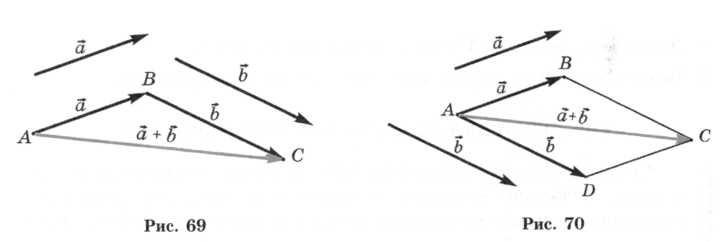
Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника(рис. 69).

Также применяется и правило параллелограмма. Оно часто используется в физике.

Если ABCD — параллелограмм (рис. 70), то + = .

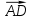
Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точки А, В, С, D, Е, F, то всегда

Определение. Два вектора, сумма которых равна нулевому вектору, называютсяпротивоположными.

Из определения следует, что у противоположных векторов соответствующие координаты имеют противоположные знаки.

Определение. Разностью векторов а и b называется такой вектор с , который в сумме с вектором bдает вектор а .

Если а (а₁; а₂; а₃) и b( b₁; b₂; b₃), то — = (а₁ –b₁; а₂ — b₂; а₃ – b₃).

Работа студентов по слайдам. Решение задач у доски по желанию.

Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Вектор: определение и основные понятия

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Определение вектора

Вектор равенство векторов координаты вектора

рис. 1

Видео:Равенство векторов. 9 класс.Скачать

Обозначение вектора

Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Длина вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Нулевой вектор

Нулевой вектор обычно обозначается как 0 .

Длина нулевого вектора равна нулю.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Коллинеарные вектора

рис. 2

Видео:9 класс, 2 урок, Координаты вектораСкачать

Сонаправленные вектора

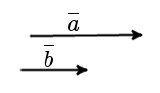рис. 3

Видео:8 класс, 41 урок, Равентво векторовСкачать

Противоположно направленные вектора

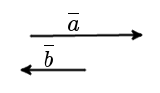рис. 4

Видео:10 класс, 39 урок, Равенство вектораСкачать

Компланарные вектора

рис. 5

Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.

Видео:Абсолютная величина вектора. Равенство векторов.Скачать

Равные вектора

рис. 6

То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:

a = b , если a ↑↑ b и | a | = | b |.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Единичный вектор

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.