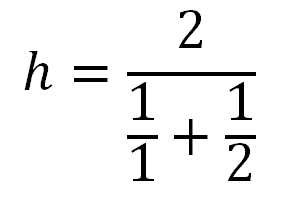Среднее гармоническое в треугольнике

Различные средние положительных. Неравенство Коши.

Горбунов Денис, 11 класс, МОУ лицей №1 г. Кунгура Пермского края

Научный руководитель: , учитель математики лицея №1

Web-адрес:http://lyceum-kungur. /works. html

В школьном курсе математики и физики изучаются средние величины (среднее арифметическое, среднее геометрическое, среднее гармоническое и среднее квадратичное).

Между ними существуют удивительные соотношения, которые исследованы учёными. О. Коши, французский математик, сопоставив две средние величины, пришёл к выводу о том, что среднее арифметическое n чисел всегда не меньше среднего геометрического этих чисел.

Неравенство Коши используется при решении уравнений, неравенств и систем методом оценок, появляется в вариантах теста ЕГЭ (например, задача С3 в 2006 году).

Развитие теории неравенств с переменными за последние сто лет привело к появлению в ней необычайного разнообразия методов и направлений, что и стало предметом моего исследования.

Работа состоит из двух частей: теоретической и практической. Теоретическая часть представлена тремя разделами: средние величины и их сравнение для двух положительных чисел; замечательные неравенства и методы решения задач.

Вторая часть – практическая, которая ставила своей целью научиться применять замечательные неравенства при решении различных заданий.

Думаю, что проделанная мною работа поможет мне успешно подготовиться к ЕГЭ и будет интересна для ознакомления выпускникам школ и увлечённым математикой людям.

Тема: Различные средние положительных. Неравенство Коши.

Цель: изучение средних величин, определение оптимальных методов решения задач со средними величинами.

1) познакомиться с историей появления средних величин,

2) дать определение средним величинам,

3) доказать алгебраически и геометрически соотношение между средними величинами,

4) рассмотреть применение неравенства Коши при исследовании свойств функций,

5) систематизировать различные методы решения нестандартных задач.

Почему я выбрал эту тему?

Когда передо мной встал вопрос выбора темы, я из всех рассматриваемых вариантов незамедлительно выбрал эту. Свой выбор я основывал на том, что эта тема поможет мне подготовиться к экзаменам и узнать много нового для себя.

II. А)Теоретическая часть

2.1.Понятие средней величины.

2.2.Из истории средних величин

2.3.Соотношение между средними величинами

2.3.1.Сравнение среднего арифметического и среднего геометрического

2.3.2.Сравнение среднего арифметического и среднего квадратичного

2.3.3.Сравнение среднего гармонического и среднего геометрического

2.3.4.Геометрическое доказательство сравнения средних величин

2.3.4.1. Среднее арифметическое и среднее квадратичное

2.3.4.2. Среднее арифметическое и среднее геометрическое

2.3.4.3. Среднее гармоническое и среднее геометрическое

2.3.4.4. Построение четырёх средних по заданным отрезкам a и b

2.3.5.Решение геометрических задач на сравнение средних величин

2.4. Средние для n положительных чисел

2.5. Замечательные пределы, порождаемые классическими средними.

2.6. Замечательное неравенство Коши

2.7.Основные методы решения задач на доказательство неравенств

2.7.1. Метод анализа

2.7.2. Метод синтеза

2.7.3. Метод от противного

2.7.4. Метод использования тождеств

2.7.5. Метод оценивания

2.7.6. Метод введения новых переменных, или метод

2.7.7. Метод введения вспомогательных функций

2.7.8. Метод уменьшения числа переменных в неравенстве и понижения степени неравенства

2.8. Применение неравенства Коши при решении задач.

2.9. Задача Дидоны и другие задачи на оптимизацию

В школьном курсе математики каждый пятиклассник встречается со средним арифметическим двух или нескольких натуральных чисел (; ;…). При изучении геометрии в восьмом классе, рассматривая прямоугольный треугольник, каждый школьник знакомится со средним геометрическим двух отрезков (). В прямоугольном треугольнике таким свойством обладают три отрезка: два катета и перпендикуляр, опущенный из вершины прямого угла на гипотенузу. С уроков физики известно, что если и — скорости на двух участках пути, то средняя скорость равна , то есть является средним гармоническим и . Существует ещё и четвёртое среднее – среднее квадратичное .

Можно выделить большой класс задач, для решения которых достаточно знать и уметь применять сравнительно несложные неравенства. К числу таких неравенств относится, прежде всего, неравенство Коши: среднее арифметическое двух положительных чисел a и b не меньше их среднего геометрического: . Наряду с неравенством Коши полезно знать следствия из него:

В неравенствах равенство достигается, если a = b. Эти неравенства эквивалентны друг другу при , .

Данные неравенства используются при решении уравнений, неравенств и систем методом оценок, появляются в вариантах теста ЕГЭ (например, задача С3 в 2006 году).

Следует отметить, что развитие теории неравенств с переменными за последние сто лет привело к появлению в ней необычайного разнообразия методов и направлений.

Я изучил большое количество литературы по данной теме, систематизировал её. Работа состоит из двух частей: теоретической и практической. Теоретическая часть представлена тремя разделами: средние величины и их сравнение для двух положительных чисел; замечательные неравенства и методы решения задач.

Вторая часть – практическая, которая ставила своей целью научиться применять замечательные неравенства при решении различных заданий.

Думаю, что проделанная мною работа поможет мне успешно подготовиться к ЕГЭ.

Понятие средней величины.

Средней величиной действительных чисел называют всякое действительное число х, удовлетворяющее условию , где m – наименьшее, а М – наибольшее среди чисел .

Средняя величина чисел только одна в том и только в том случае, когда .

Средним геометрическим действительных неотрицательных чисел называют такое действительное неотрицательное число .

Средним арифметическим действительных чисел называют действительное число .

Средним гармоническим действительных положительных чисел называют положительное число .

Средним квадратическим (квадратичным) действительных чисел называют неотрицательное действительное число.

Если рассмотреть два положительных числа a и b, то эти средние величины будут выглядеть следующим образом:

среднее арифметическое: среднее геометрическое: среднее гармоническое: среднее квадратичное:

Можно рассмотреть следующие задачи.

Задачи № 1. Определить среднюю скорость туриста на всем пути, если от пункта А до пункта В он шёл со скоростью , а обратно – со скоростью .

Решение. Обозначим символом S расстояние между пунктами А и В, тогда

— время туриста от А до В, а

— время туриста обратно.

+ — время, затраченное на весь путь.

Тогда

Получили, что есть среднее гармоническое скоростей и .

Задача № 2. В прямоугольном треугольнике АВС из вершины С на гипотенузу опущен перпендикуляр CD, который делит гипотенузу на отрезки AD = a; BD = b. Выразить через a и b:

2) DE (где Е – есть точка пересечения окружности, описанной около треугольника АВС, и перпендикуляра, проведённого к АВ через центр окружности)

3) СК (где точка К — есть основание перпендикуляра, опущенного из точки D на r = СО.

Решение.

1) ∆АВС – прямоугольный, поэтому АВ – диаметр окружности

АВ = a + b, О – центр окружности, то есть АО = ОВ = ОЕ =

Получили, что ЕО = является средним арифметическим двух отрезков, длины которых a и b.

2)CD┴АВ (по условию), следовательно, по свойству перпендикуляра, опущенного из вершины прямого угла на гипотенузу, CD²=ADDB. Значит

, то есть .

CD является средним геометрическим двух отрезков, длины которых равны a и b.

3) ∆OED – прямоугольный, так как EO ┴ АВ (по условию)

(как радиус окружности)

По теореме Пифагора

, то есть DE является средним квадратичным для двух отрезков, длины которых a и b.

4) ∆DOC – прямоугольный, так как CD ┴ АВ. Проведём

┴ СО.

По свойству прямоугольного треугольника CD² = CO CK, то есть

, то есть СК – среднее гармоническое для a и b.

Из решения этой задачи видно, что для двух отрезков a и b можно найти четыре зависимости: среднее квадратичное, среднее гармоническое, среднее арифметическое, среднее геометрическое.

В какой же зависимости они находятся друг от друга?

Из истории средних величин.

Когда возникли понятия средних величин в математике, точно не известно. Но предполагают, что уже вавилоняне более трех тысяч лет назад использовали их при вычислении квадратных корней. В дошедших до нас табличках квадратные корни из натуральных чисел фактически вычислены по известной нам формуле:

если N = β² + r, то = .

Восстанавливая ход рассуждений вавилонян, современные учёные пришли к выводу, что они брали среднее арифметическое чисел β и . В самом деле, если обозначить , то β= .

Много позже древнегреческий математик Герон (I в.) в своей «Метрике», применяя тот же метод приближённого вычисления квадратного корня, писал, что если результат получается со слишком большой погрешностью, то указанную процедуру можно повторить, т. е. взять среднее арифметическое чисел βи .

Применим этот алгоритм к вычислению квадратного корня из натурального числа, записав его в виде произведения двух натуральных чисел: N = ab (при простом N один из сомножителей равен 1). В качестве первого приближения значения возьмём , затем следуя рекомендации Герона, найдем , которое оказывается средним гармоническим чисел a и b.

Также средние величины были известны и античным математикам. В одном из математических тестов, которые приписывают древнегреческому математику Архиту (ок. 428 – 365 г. г. до н. э.), среднее арифметическое А, среднее геометрическое G и среднее гармоническое Н определялись как равные члены соответственно арифметической, геометрической и гармонической пропорций:

(a – H) : a = (H – b) : b.

Из этих равенств получаем

; ; .

Свои названия перечисленные средние величины получили в античные времена. Аристо– 322 г. г. до н. э.), великий философ древности, объяснял происхождение названий так. Среди чисел каждое последующее больше предыдущего на постоянное число (при условии a 1)

Применим неравенство Коши для слагаемых и .

(х > 1)

Таким образом правая часть уравнения не превосходит 2, а левая часть не меньше 2. Равенство достигается если обе части равны двум, то есть

Значит при х = 2.

Нахождение наибольшего и наименьшего значения функции.

С помощью неравенства Коши можно находить наибольшее и наименьшее значения функции без использования производной. Для этого потребуются утверждения, вытекающие непосредственно из неравенства Коши:

1. Равенство в неравенстве Коши достигается, когда все, учавствующие в нём числа одинаковы.

2. Если сумма положительных чисел равна а, то произведение этих чисел принимает наибольшее значение при и это наибольшее значение равно .

3. Если произведение положительных чисел равно b, то их сумма принимает наименьшее значение при и это значение равно .

Задача № 1. Найти наименьшее значение функции , .

Решение. Представим функцию в виде суммы слагаемых

.

Найдем произведение этих слагаемых

.

Это означает, что своё наименьшее значение сумма слагаемых принимает при , то есть при .

.

Ответ: у = 4 – наименьшее значение функции, которое достигается при х = 1.

Задача № 2. Найти наибольшее значение функции на отрезке .

Решение. Возведём функцию в квадрат, получим:

, разделим обе части на 4:

.

Представим произведение в виде произведения

.

Найдём сумму этих множителей

,

то есть сумма принимает постоянные значения. Следовательно, функция , а значит и функция достигает наибольшего значения при .

Найдём значения функции в этих точках

Следовательно, наибольшее значение функции равно при .

Задача № 3. При каких значениях х функция достигает наибольшего значения?

Решение. Запишем функцию в виде

.

Найдем сумму этих 5 сомножителей

.

Применим неравенство Коши для n = 5

Следовательно, функция достигает наибольшего значения равного , если

Ответ: при функция достигает наибольшее значение.

Задача № 4. Найти наибольшее и наименьшее значение функции .

Решение. Найдём область определения функции .

1) — наименьшее значение, так как .

2) Применим неравенство Коши для n = 2 для слагаемых и .

, то есть функция имеет наибольшее значение , оно достигается, если

Действительно, .

Ответ:

.

Основные методы решения задач на установление истинности неравенств с переменными.

Это метод, основанный на анализе исследуемого неравенства, причём таком анализе, с помощью которого «обратимыми» рассуждениями строят цепочку переходов от доказываемого неравенства (через ряд промежуточных) к некоторому очевидному (благодаря ранее полученным результатам) неравенству.

Рассмотрим решение задачи методом анализа.

Задача № 1. Доказать, что для любых действительных чисел a, b, c, d таких, что и , выполнимо неравенство .

Решение. Рассмотрим цепочку переходов от одного неравенства к другому, ему равносильному, учитывая, что и по условию.

.

Возведём обе части в квадрат, так как они неотрицательны:

Подставим значения c² и d² из условия .

Получили очевидное неравенство.

Это метод, основанный на получении (синтезировании) неравенства (которое требуется обосновать) из опорных (базисных) неравенств и методов их установления.

Решим задачу, используя метод синтеза.

Задача № 2. Докажите, что для любых неотрицательных a, b, c справедливо неравенство

.

Решение. Запишем три неравенства, устанавливающие зависимость между средним арифметическим и средним геометрическим двух неотрицательных чисел

; ;

Перемножим почленно полученные неравенства, так как их левая и правая части неотрицательны

Суть метода состоит в том, что предполагается выполнение всех условий задачи, а вот само неравенство не выполнено. После чего проводится цепочка равносильных преобразований и выявляется гипотеза, устанавливающая противоречия о выполнении данного неравенства.

Рассмотрим задачу № 1, решённую методом анализа. Решим её методом от противного.

Задача № 1. Доказать, что для любых действительных чисел a, b, c, d таких, что и , выполнимо неравенство .

Решение. Пусть условия задачи выполнены, то есть и и .

Допустим, что данное неравенство неверно, а при данных условиях выполняется следующее неравенство:

.

Это неравенство равносильно совокупности неравенств:

Умножим обе части неравенства на 2 и правую часть представим в виде суммы 1+1:

Подставим из условия значения 1:

Перенесём всё в левую часть и применим формулу квадрат суммы:

Получили совокупность неравенств, которая решений не имеет, значит предположение о выполнении неравенства неверно, то есть .

Метод использования тождеств.

Суть метода состоит в том, что данное неравенство путём равносильных преобразований приводится к очевидному тождеству.

Рассмотрим решение задачи этим методом.

Задача № 3. Докажите, что для любых действительных чисел a и b справедливо неравенство .

Решение. Выделим в левой части неравенства полный квадрат

.

При любых действительных a и b это выражение неотрицательно, значит и данное неравенство выполнимо, то есть .

Метод оценивания (метод усиления или ослабления).

Метод усиления заключается в последовательном переходе от меньшей функции к большей (как говорят, оценивающей «сверху» эту меньшую функцию). Такие «переходы» приводят к получению так называемого более сильного неравенства, то есть неравенства с большей правой частью, нежели у его предшественников – неравенств. Иначе говоря, если требуется доказать неравенство вида A B и удалось установить, что A > C и C > B, где А, В, С – функции от соответствующих переменных, принимающих произвольные значения из оговорённой области определения, то тем самым оказывается установленным и неравенство A > B.

Аналогичный подход можно применять для доказательства нестрогих неравенств.

Вернёмся к задаче № 1 и решим её третьим способом – методом усиления.

Задача № 1. Доказать, что для любых действительных чисел a, b, c, d таких, что и , выполнимо неравенство .

Решение. Применим свойство модуля к левой части неравенства .

Представим слагаемые в правой части в виде корня:

К этим выражениям применим зависимость между средним арифметическим и средним геометрическим

.

Таким образом, .

Метод введения новых переменных, или метод подстановки.

Суть метода состоит в том, что в данном неравенстве какое – либо выражение обозначается новой переменной, а затем полученное неравенство относительно новой переменной доказывают, используя уже известные методы.

Рассмотрим задачу на применение данного метода.

Задача № 4. Доказать, что для любых положительных a, b, c справедливо неравенство

.

Решение. Пусть ; ; .

Найдём сумму новых переменных x+y+z и применим зависимость между средним арифметическим и средним геометрическим

; ;

Подставим значения x, y и z:

Так как a>0, b>0, c>0 по условию, то

.

Метод введения вспомогательных функций с целью использования их свойств.

Суть метода заключается в том, что в неравенстве одно значение переменной фиксируется как параметр, а другое значение обозначается через переменную х. В результате чего получаем вспомогательную функцию относительно х. Для доказательства условия задачи следует выяснить множество значений полученной вспомогательной функции.

Решим задачу на применение этого метода.

Задача № 3. Докажите, что для любых действительных чисел a и b справедливо неравенство .

Решение. Решим эту задачу вторым способом, методом введения вспомогательной функции. Пусть b – фиксированное действительное число, параметр, а = х, тогда получим функцию , которая является квадратичной, ветви параболы направлены вверх.

, поэтому квадратичная функция принимает только неотрицательные значения, , значит , то есть .

Метод уменьшения числа переменных в неравенстве и понижение степени неравенства.

Суть метода заключается в том, что уменьшается число переменных в неравенстве с помощью метода подстановки и выполнения арифметических действий и применения очевидных тождеств.

Рассмотрим доказательство неравенства этим методом.

Задача № 1. Докажите, что для любых положительных a, b, c справедливо неравенство: .

Решение. Разделим правую и левую части неравенства на с3(c > 0, а значит и с3 > 0) и введём новые переменные:

В результате получим новое неравенство

; ,

доказательство которого равносильно доказательству исходного неравенства. Перепишем его левую часть в следующем виде:

и введём новые переменные:

; , причём x > 0, y > 0 и x² ≥ 4y. Теперь получили неравенство вида

, где ,

чьё обоснование позволяет сделать вывод и о справедливости исходного неравенства. Существенными достижениями в результате сделанных преобразований явились следующие: уменьшилось число переменных, а степень относительно переменного у оказалась равна единице. Преобразовав полученное неравенство к виду

и введя в рассмотрение следующую вспомогательную функцию (считая х произвольным положительным фиксированным числом) с областью определения R можем заключить, что при любом фиксированном значении х графиком этой функции будет прямая. Следовательно, её наименьшее на отрезке достигается на одном из его концов. Найдем значение функции в этих точках:

и . Таким образом значения функции на концах отрезка положительны при x > 0, а это доказывает истинность исходного неравенства.

Применение неравенства Коши при доказательстве неравенств

Задача № 1. Доказать неравенство

при b ≥ 0.

Решение. Умножим обе части неравенства на 4:

Применим неравенство Коши к числам :

Задача № 2. Доказать неравенство:

, при a ≥ 0; b ≥ 0; c ≥ 0.

Решение. Применим неравенство Коши для каждых двух чисел:

Обе части неравенств неотрицательны, поэтому сложим их почленно:

Задача №3. Доказать неравенство

, при a ≥ 0; b ≥ 0; c ≥ 0.

Решение. Применим неравенство Коши для каждой суммы:

Обе части неравенств неотрицательны, поэтому перемножим их левые и правые части:

.

Задача № 4. Доказать неравенство

, при n ≥ 2.

Решение.

Применим неравенство Коши к числам 1, 2, 3,…, (n-1), n:

.

В числителе правой части сумма n членов арифметической прогрессии. Она равна .

.

Задача Дидоны и другие задачи на оптимизацию.

Ещё в глубокой древности люди задумывались, как, имея в своём распоряжении тот или иной ресурс (например, деньги), так им распорядиться (вложить деньги в «дело», дать в долг под проценты, раздать нищим, закопать в собственном огороде и т. д.), чтобы получить наибольшую пользу и наименьший ущерб для себя.

То, что подобные задачи на оптимизацию встречались ещё в античные времена, донесли до нас мифы Древней Греции и Рима. Причём интуиция и опыт человеческий уже тогда позволяли «нащупать» решения подобных задач, дающие оптимальный или близкий к оптимальному результат.

Вот один из мифов, наполовину древнегреческий, наполовину древнеримский. Дочь царя Тира, Дидона, жена жреца храма Геракла Акербаса вынуждена была бежать из Финикии в Северную Африку. Причина бегства – её брат, Пигмалион, позарившийся на богатства её мужа и убивший его. Многочисленные сокровища мужа и многочисленные спутники Дидоны нуждались в пристанище. Чтобы обрести его, беглянка купила у берберийского царя Ярба землю, причём по условию она в обмен на немалые сокровища могла взять ровно столько земли, сколько покроет одна бычья шкура. Чтобы выполнить это условие и получить достаточно обширную территорию, Дидона разрезала шкуру на тонкие ремни, сделала из них длинную верёвку и «окружила» ею изрядный кусок земли, естественно, круглой формы, на котором основала Карфаген. Любопытно, что карфагенская цитадаль называется Бирса (Бирсу), что в переводе с греческого означает «шкура». Однако дальнейшая судьба Дидоны была трагическая: она покончила жизнь самоубийством.

Но вернёмся к математике. Задача, которую решила Дидона, может быть сформулирована так: найти замкнутую кривую, ограничивающую часть плоскости с максимальной площадью. В таком общем виде эта задача слишком сложна. Однако, если упростить задачу Дидоны и договориться о более конкретных формах участка земли, то возникают задачи, чьи решения могут быть получены без обращения к высшей математике, при помощи замечательных неравенств. Задачи типа задачи Дидоны называют в математике изопериметрическими задачами (от греческих слов isos – равный и perimetrio – измеряю вокруг).

Задача № 1. Найдите из множества всех прямоугольников с заданным периметром тот, чья площадь наибольшая.

Решение. Обозначим стороны искомого прямоугольника символами x и y, а его периметр – символом р > 0, тогда задача стоит так: при каких x и y – положительных числах, удовлетворяющих условию , их произведение будет наибольшим. Применим неравенство Коши: , , т. е. . Итак, подозрительным на наибольшее значение произведения является число , но достигается ли оно при допустимых x и y? Да, достигается. Полагая из равенства , получаем .

Задача № 2. Найдите среди всех треугольников с заданным периметром тот, чья площадь наибольшая.

Решение. Если обозначим стороны произвольного треугольника x, y, z, то по условию

, и ,

где фиксированное число . Требуется определить наибольшее значение выражения

.

Применим неравенство Коши для n = 3

,

то есть , причём равенство достигается тогда и только тогда, когда , то есть для равностороннего треугольника.

Рассмотрим задачу С3 , которая предлагалась в тесте ЕГЭ в 2006 году.

Задача № 3. Требуется разместить на земле участок площадью 3400 м2 , который состоит из трёх прямоугольных частей и имеет форму многоугольника ABCDFGHM, изображённого на рисунке, где ВС = 20 м, CD = 15 м, GH = 30 м и HM ≥ 40 м. Найдите наименьшее значение периметра такого участка и какие – либо значения длин АК, AL и HM, при которых периметр является наименьшим.

Площадь участка равна S = 3400, а его периметр равен периметру Р прямоугольника KALF . Обозначим AK = x, х > 0; AL = y, y > 0

и HM = z, z ≥ 40. Тогда ,

.

Поэтому и .

Применим неравенство Коши для двух слагаемых

,

, ,

Равенство достигается при , то есть .

, то есть

и это значение достигается при

Ответ. Р = 280 м; АК = 70; AL = 70; HM = 40.

Неравенства для средних и сами средние широко применяются не только в алгебре, геометрии, математическом анализе, но и в статистике, в теории вероятностей (оттуда пришло среднее квадратичное), при обработке результатов измерений. Средняя урожайность, средняя плотность населения, средняя температура, средняя рождаемость, средняя глубина реки, – это примеры средних величин, постоянно окружающих нас.

Неравенства играют фундаментальную роль в большинстве разделов современной математики, без них не может обойтись ни физика, ни математическая статистика, ни экономика. По словам Э. Беккенбаха, «…основные результаты математики чаще выражаются неравенствами, а не равенствами». Однако до сих пор нет хорошо разработанной, достаточно общей «теории неравенств», хотя для обоснования отдельных классов неравенств такую теорию удалось создать – это и некоторые разделы выпуклого анализе, и теория мажоризации, и ряд других. Так или иначе, но неравенства встречаются как в классических разделах математики (в геометрии, в дифференциальном и интегральном исчислении, в теории чисел), так и в достаточно современных её разделах (теория автоматов, теория кодирования). Количество новинок среди даже не неравенств, а классов неравенств увеличивается необычайно быстро, стремительно и неудержимо.

Можно было бы указать имена тех учёных, кто получил первым тот или иной результат, касающийся неравенств. Однако многие из результатов были получены и применены как некоторые вспомогательные средства в какой – либо работе по геометрии, астрономии, или физике, а затем переоткрыты много лет спустя. Это послужило причиной тому, что даже названия многих замечательных неравенств не устоялись, а также терминология вообще. В разных странах и в разных математических школах одно и то же неравенство называют по – разному и приписывают его открытие разным математикам. Зачастую давно полученное неравенство вдруг оказывается частным случаем и более общего, да и более молодого по срокам появления неравенства. Например, невозможно найти первооткрывателя того фундаментального факта, что квадрат любого действительного числа всегда неотрицателен, а значит для любых действительных чисел a и b справедливо соотношение , а значит , откуда получается знаменитое соотношение между средним арифметическим и средним геометрическим, то есть , где .

1. , Курляндчич // Математика в школе, 1990, № 3.

2. Неравенство Коши о среднем арифметическом и геометрическом // Математика, 1999, № 20.

3. Берколайко неравенства Коши при решении задач // Квант, 1975, № 4.

4. Волошинов и искусство – М.: Просвещение, 1992.

5. Глейзер математики в средней школе. – М.: Просвещение, 1970.

6. Глейзер математики в школе. – М.: Просвещение, 1982.

7. Числовые средние и геометрия // Квант, 1990, № 9.

8. Гомонов неравенства: способы получения и примеры применения. 10 – 11 классы: учебное пособие. – М.: Дрофа, 2006.

9. Геометрические задачи на максимум и минимум // Квант, 2005, № 2.

10. Дубровский об общей внешней касательной к окружностям, касающимся внешним образом // Квант, 1986, № 2.

11. Треугольники и неравенства // Квант, 2005, № 2.

12. Геометрические доказательства теорем о средних // Квант, 1981, № 2.

13. Замечательные пределы, порождаемые классическими средними // Квант, 1981, № 9.

14. Замечательные пределы, порождаемые классическими средними // Квант, 1981, № 9.

15. Кушнир одной задачи // Квант, 1986, № 9.

16. Среднее. В среднем. О среднем… // Математика, 2000, № 8.

17. Описанная трапеция и средние //Квант, 1972, № 8.

18. О применении одного неравенства // Квант, 1997, № 2.

19. Сивашинский в задачах. – М.: Наука, 1967.

20. Скопец различных средних двух положительных чисел // Квант, 1979, № 2.

21. Неравенства // Математика, 2006, № 5.

22. Классические неравенства в задачах // Математика, 2005, № 15.

23. Сложные задачи вступительных экзаменов в МГУ: неравенства о средних // Математика, 2006, № 10.

24. Неравенства Коши о средних арифметическом и геометрическом // Математика, 2000, № 7, № 8.

25. Неравенства Коши о среднем арифметическом и геометрическом // Математика, 2000, № 7.

26. Шлейфер неравенства // Математика в школе, 1994, № 3.

27. Энциклопедический словарь юного математика / Сост. . – М.: Педагогика, 1989.

28. Как доказать неравенство // Квант, 1997, № 2.

В ходе исследования я узнал много нового для себя, научился решать задачи по данной теме. Наиболее трудным в работе показалась работа с литературой и систематизация знаний. Хотелось бы поблагодарить всех, кто помогал мне в ходе работы.

В дальнейшем мне хотелось бы провести более глубокое исследование по этой теме.

Я считаю, что неплохо поработал, цели достиг, с задачами справился. Конечно, в работе есть недочеты, но, наверное, это связано с отсутствием опыта участия в подобных конференциях.

Видео:Среднее гармоническое чисел. Работа с формулойСкачать

Гармоническое Среднее

Видео:КАК НАЙТИ СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ? ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Что такое Гармоническое Среднее?

Гармоническое среднее – это разновидность среднего численного значения. Он рассчитывается путем деления количества наблюдений на обратную величину каждого числа в серии. Таким образом, гармоническое среднее является величиной, обратной среднему арифметическому обратных величин.

Среднее гармоническое значение 1, 4 и 4 равно:

Краткая справка

Обратное значение числа n равно 1 / n.

Видео:Среднее гармоническое. Средняя скорость. Причём тут планиметрия?Скачать

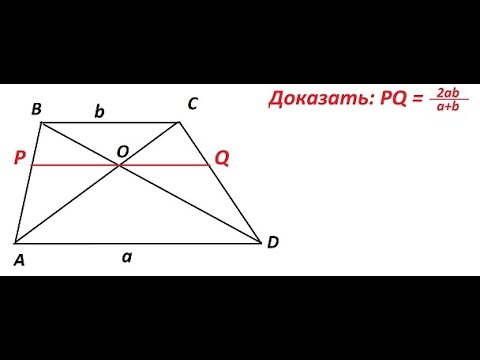
Основы гармонического среднего

Гармоническое среднее помогает найти мультипликативные отношения или отношения делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения при продолжительности нескольких поездок).

Средневзвешенное гармоническое среднее используется в финансах для усреднения мультипликаторов, таких как соотношение цены и прибыли, поскольку оно придает одинаковый вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих соотношений даст больший вес высоким точкам данных, чем низким точкам данных, потому что соотношение цена / прибыль не нормализуется по цене, в то время как прибыль выравнивается.

Гармоническое среднее – это взвешенное гармоническое среднее, где веса равны 1. Взвешенное гармоническое среднее значений x 1 , x 2 , x 3 с соответствующими весами w 1 , w 2 , w 3 задается как:

Ключевые моменты

• Гармоническое среднее – это величина, обратная среднему арифметическому обратных величин.
• Гармонические средние используются в финансах для усреднения данных, например, ценовых мультипликаторов.
• Гармонические средства также могут использоваться рыночными техниками для выявления паттернов, таких как последовательности Фибоначчи.

Видео:Среднее пропорциональное!? А что это!?Скачать

Сравнение среднего гармонического и среднего арифметического и среднего геометрического

Другие способы вычисления средних значений включают простое среднее арифметическое и среднее геометрическое. Среднее арифметическое – это сумма серии чисел, деленная на количество этой серии чисел. Если бы вас попросили найти среднее (арифметическое) среднее количество баллов за тест, вы просто сложите все баллы учащихся, а затем разделите эту сумму на количество учащихся. Например, если пять студентов сдали экзамен и их баллы составили 60%, 70%, 80%, 90% и 100%, средняя арифметическая оценка по классу будет 80%.

Среднее геометрическое среднее из набора продуктов, расчет которых обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как «произведение корня n-й степени из n чисел». Среднее геометрическое должно использоваться при работе с процентами, которые выводятся из значений, в то время как стандартное среднее арифметическое работает с самими значениями.

Гармоническое среднее лучше всего использовать для таких дробей, как ставки или кратные.

Видео:Математика | Метрические соотношения в прямоугольном треугольникеСкачать

Пример среднего гармонического

В качестве примера возьмем две фирмы. Один имеет рыночную капитализацию 100 миллиардов долларов и прибыль 4 миллиарда долларов (P / E 25), а другой – рыночную капитализацию 1 миллиард долларов и прибыль 4 миллиона долларов (P / E 250). В индексе, составленном из двух акций, с 10% инвестиций в первую и 90% во вторую, коэффициент P / E индекса равен:

Видео:Задача, которую исключили из экзамена в АмерикеСкачать

Среднее гармоническое

Среднее гармоническое — один из способов определения среднего значения числового ряда (наряду с медианой и средним арифметическим). Мы сделали калькулятор, который может рассчитать среднее гармоническое двух, трех — да любого количества чисел.

Рассчитывается среднее гармоническое по простой формуле и является обратной величиной к среднему от обратных к числам.

Среднее гармоническое удобно применять для решения задач, которые начинаются словами «первую половину пути автомобиль проехал со скоростью…». Например, первую половину пути автомобиль проехал со скоростью 60 км/ч вторую 90 км/ч. Найдите среднюю скорость. Просто введите в калькулятор два числа — 60 и 90 и получите ответ — 72 км/ч.

Видео:РАЗБИРАЕМ СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Калькулятор среднего гармонического

Видео:170 Алгебра 8 класс Найдите среднее гармоническое чиселСкачать

Как найти среднее гармоническое чисел

Лучше показать это на примере. Найдем среднее гармоническое двух чисел 1 и 2. Подставив значения в формулу получим такое выражение:

Здесь в числителе количество чисел (2), а в знаменателе сами числа. В результате расчета получаем, что среднее геометрическое чисел 1 и 2 равно 1,6666… или 1,(6).

💡 Видео

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Вариант 52, № 2. Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольникеСкачать

Задача, которую не запретили в школах. Делим треугольник Как построить среднее геометрическоеСкачать

Тема 6. Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольникеСкачать

Средние величины. Средняя гармоническая.Скачать

Задачи на среднее геометрическое (пропорциональное). Геометрия 8 9 классСкачать

Высота как среднее геометрическое отрезков | Профильная математикаСкачать

Все средние в одной полуокружностиСкачать

Математика для всех. Алексей Савватеев. Лекция 3.2. Гармонический рядСкачать

пропорциональные отрезки в ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ 8 классСкачать

Неравенства. Введение | Ботай со мной #046 | Борис Трушин !Скачать

Подобие прямоугольных треугольников. Среднее геометрическое (пропорциональное). Геометрия 8-9 классСкачать