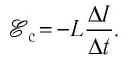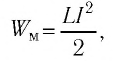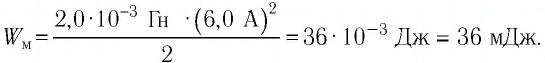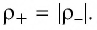Для описания магнитного поля используются две его основные характеристики — индукция B → и напряженность H → . Эти величины связаны между собой. Рассмотрим, что такое напряженность магнитного поля, чему она равна, каков физический смысл этой величины.
- Напряженность магнитного поля
- Физический смысл напряженности магнитного поля
- Циркуляция вектора напряженности магнитного поля
- Электродинамика — основные понятия, формулы и определения с примерами
- Электростатика
- Электрический заряд и закон сохранения электрического заряда
- Взаимодействие точечных зарядов и закон Кулона
- Взаимодействие системы точечных зарядов
- Диэлектрическая проницаемость вещества
- Электростатическое поле
- Напряжённость электростатического поля. Принцип суперпозиции
- Линии напряжённости электростатического поля
- Работа силы однородного электростатического поля
- Потенциальная энергия заряда в электростатическом поле
- Разность потенциалов электростатического поля
- Конденсаторы
- Электроёмкость конденсатора
- Электроёмкость плоского конденсатора
- Энергия электростатического поля конденсатора
- Применение конденсаторов
- Постоянный электрический ток
- Условия существования постоянного электрического тока
- Сторонние силы
- Электродвижущая сила источника тока
- Закон Ома для полной электрической цепи
- Различные режимы работы электрической цепи
- Коэффициент полезного действия источника тока
- Магнитное поле
- Действие магнитного поля на проводник с током
- Взаимодействие проводников с током
- Действие магнитного поля на рамку с током
- Индукция магнитного поля
- Направление индукции магнитного поля
- Линии индукции магнитного поля
- Направление линий индукции магнитного поля
- Определение направления индукции магнитного поля
- Сила Ампера
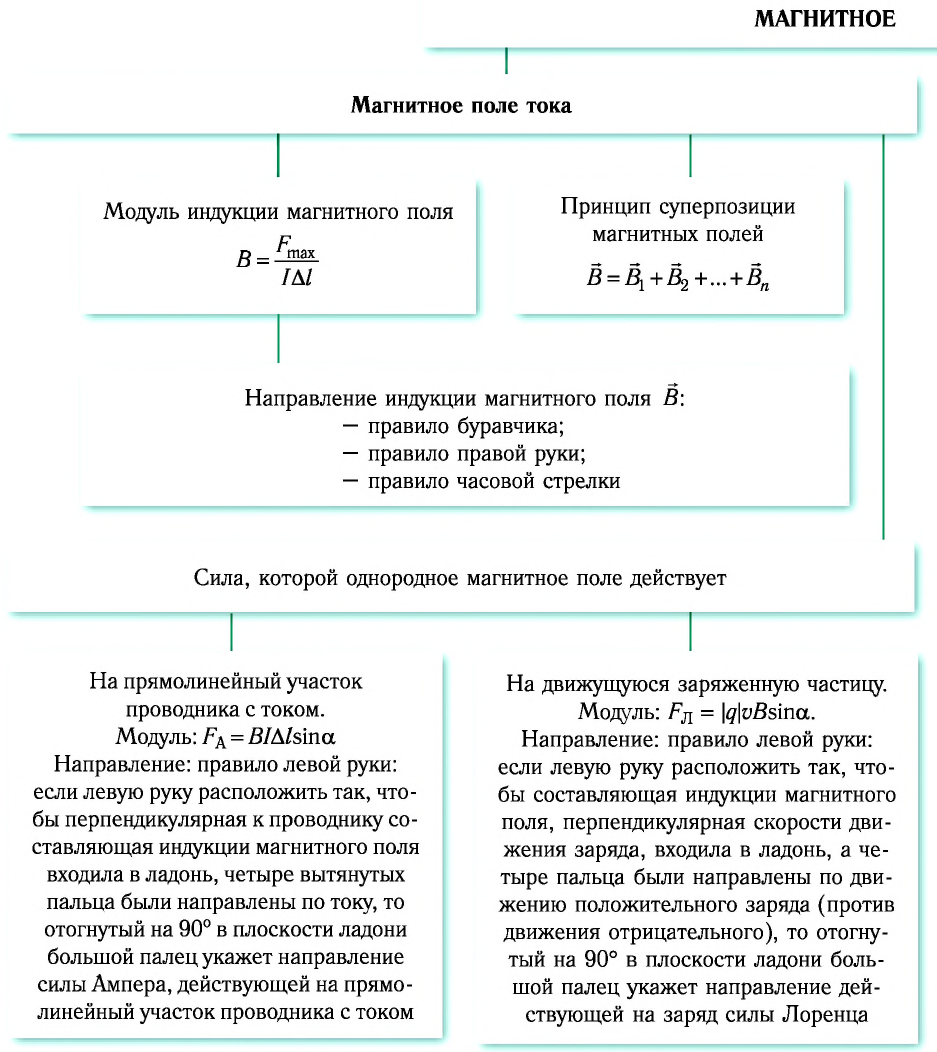
- Модуль индукции магнитного поля
- Закон Ампера
- Принцип суперпозиции магнитных полей
- Сила Лоренца
- Движение заряженных частиц в однородном магнитном поле
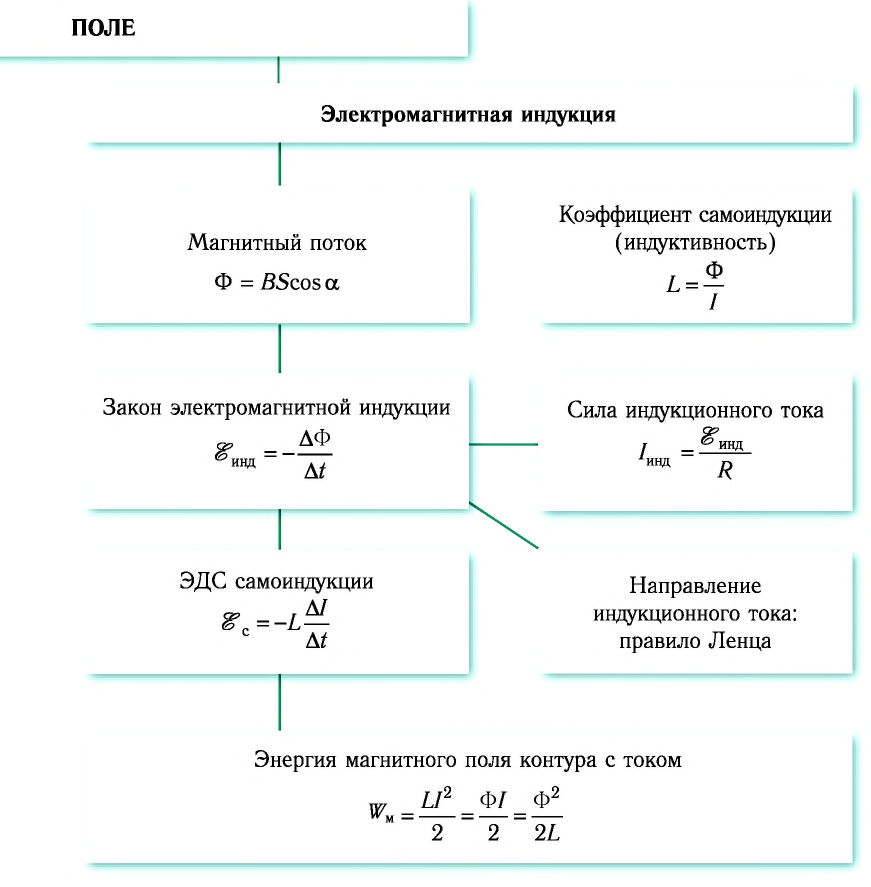
- Магнитный поток
- Явление электромагнитной индукции
- Правило Ленца
- Направление индукционного тока.
- Закон электромагнитной индукции
- Явление самоиндукции
- Энергия магнитного поля
- Электрический ток в различных средах
- Электрический ток в металлах
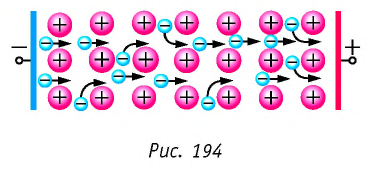
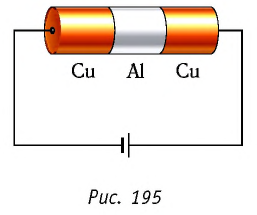
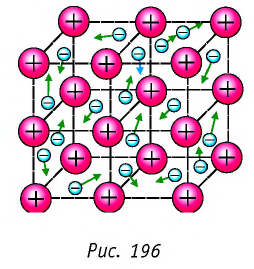
- Природа электрического тока в металлах
- Зависимость сопротивления металлов от температуры
- Сверхпроводимость
- Электрический ток в электролитах
- Природа электрического тока в электролитах
- Техническое применение электролиза
- Электрический ток в газах
- Природа электрического тока в газах
- Виды самостоятельного газового разряда и их применение
- Плазма
- Электрический ток в полупроводниках
- Зависимость сопротивления полупроводников от температуры и освещённости
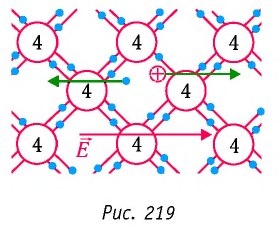
- Природа электрического тока в полупроводниках
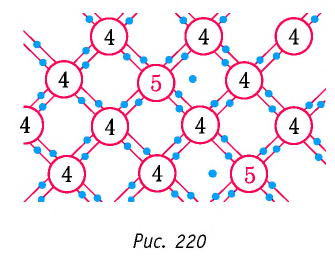
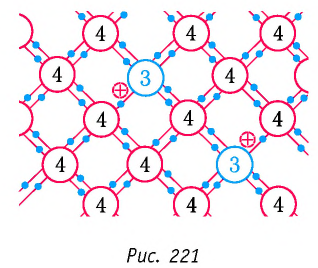
- Примесная проводимость полупроводников
- Техническое применение полупроводников
- Магнитное поле в веществе. Теорема о циркуляции векторов В и H
- 📺 Видео
Видео:Основные физические понятия технической электродинамики, 1978Скачать
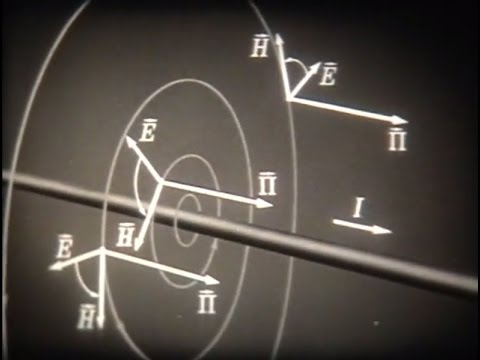
Напряженность магнитного поля
Напряженность магнитного поля — векторная физическая величина, в общем случае равная разности векторов индукции магнитного поля B → и намагниченности P m → .
Напряженность обозначается буквой Н → . Единица измерения напряженности магнитного поля в системе СИ — ампер на метр ( А м п е р м е т р ).
Формула напряженности магнитного поля:
Н → = 1 μ 0 B → — P m → .
Здесь коэффициент μ 0 — магнитная постоянная. μ 0 = 1 , 25663706 Н А 2 .
Видео:1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

Физический смысл напряженности магнитного поля
Индукция магнитного поля — силовая характеристика. Индукция определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью.
Напряженность поля характеризует густоту силовых линий (линий магнитной индукции).
Физический смысл напряженности магнитного поля
В вакууме или при отсутствии среды, способной к намагничиванию (например, в воздухе) напряженность магнитного поля совпадает с магнитной индукцией с точностью до коэффициента μ 0 .
В средах, способных к намагничиванию (магнетиках) напряженность несет смысл как бы «внешнего поля». Она совпадает с вектором магнитной индукции, который был бы, если бы магнетика не было.
Видео:1.3 Классификация сред в электродинамикеСкачать

Циркуляция вектора напряженности магнитного поля
Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля — своеобразный аналог теоремы Гаусса о циркуляции вектора напряженности электрического поля.
Теорема о циркуляции магнитного поля
Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна алгебраической сумме токов проводимости, охваченных контуром, по которому рассматривается циркуляция.
Определить циркуляцию вектора напряженности для замкнутого контура L .
I 1 = 5 A , I 2 = 2 A , I 3 = 10 A , I 4 = 1 A .
По теореме о циркуляции:
Рассматриваемый контур охватывает токи I 1 , I 2 , I 3 .
Подставим значения c учетом указанных на рисунке направлений токов и вычислим циркуляцию:
∮ H → d r → = ∑ I m = 5 A 12 A + 10 A = 13 A .
Магнитное поле — вихревое поле, которое не является потенциальным. Циркуляция вектора напряженности в общем случае отлична от нуля.
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Электродинамика — основные понятия, формулы и определения с примерами
Электродинамика — раздел физики, в котором изучают электромагнитное взаимодействие между электрически заряженными телами и частицами.
Термин «электродинамика» ввёл в физику французский учёный Андре-Мари Ампер (1775-1836) в 1822 г.
При изучении электродинамики вы познакомитесь с законами взаимодействия тел (частиц), обладающих электрическими зарядами, особенностями упорядоченного движения заряженных частиц, физическими величинами, характеризующими электрические и магнитные поля.
В разделе «Электродинамика» вам предстоит изучить следующие темы: «Электростатика», «Постоянный электрический ток», «Магнитное поле. Электромагнитная индукция» и «Электрический ток в различных средах».
Содержание:
Электродинамика:
Все известные физические явления связаны с тем пли иным взаимодействием тел пли частиц. Например, движение Луны вокруг Земли, падение тел на поверхность Земли, отклонение отвеса от вертикального направления вблизи массивной горы обусловлены гравитационным взаимодействием этих тел. Гравитационному взаимодействию подвержены все тела, однако заметным оно становится только тогда, когда хотя бы одно из взаимодействующих тел обладает достаточно большой массой.
Молекулы любого вещества также участвуют во взаимном притяжении, обусловленном силами всемирного тяготения. Но поскольку массы молекул очень малы, этим взаимодействием обычно пренебрегают. Притяжение и отталкивание молекул, обеспечивающие существование твёрдых и жидких тел, имеют совсем другую природу — электромагнитную.
Электромагнитное взаимодействие осуществляется посредством особого вида материи — электромагнитного поля — совокупности двух взаимосвязанных полей: электрического и магнитного.
Электромагнитное взаимодействие проявляется во всех электрических, магнитных и оптических явлениях. Благодаря ему вы видите окружающий мир, так как свет — одно из проявлений электромагнитного поля. Этим же взаимодействием обусловлены силы упругости и силы трения, известные вам из механики. Электромагнитное взаимодействие определяет свойства веществ в различных агрегатных состояниях и их химические превращения. Поскольку молекулярные силы электромагнитные по природе, то практически все биологические явления обусловлены электромагнетизмом.
Видео:Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Электростатика
Электростатика — раздел электродинамики, в котором изучают взаимодействие неподвижных в некоторой инерциальной системе отсчёта электрически заряженных тел, распределение заряда на которых не изменяется со временем, а также электростатические поля, создаваемые зарядами таких тел.
Термин «электростатика» введён Ампером в 1822 г.
Фундаментом электростатики являются экспериментальные научные факты, отражающие поведение заряженных тел при их электрическом взаимодействии. Ядро электростатики составляют закон сохранения электрического заряда, опытным путём установленный в 1759 г. петербургским академиком Францем Эпинусом (1724—1802), и закон взаимодействия покоящихся точечных зарядов, экспериментально открытый в 1785 г. французским учёным Шарлем Кулоном (1736-1806).
Электрический заряд и закон сохранения электрического заряда
Что означает наличие электрического заряда у тела или частицы? Как взаимодействуют электрически заряженные тела?
О том, что янтарь, потёртый о шерсть, приобретает свойство притягивать лёгкие предметы (рис. 94), знали ещё древние греки. Однако только в 1600 г. лейб-медик королевы Англии доктор медицины Уильям Гильберт в книге «О магните, магнитных телах и большом магните — Земле» дал первое систематизированное описание свойств электрических и магнитных материалов. Гильберт продемонстрировал, что кроме янтаря свойством притягивать лёгкие предметы обладают после натирания алмаз, сера, фарфор и многие другие тела. Он назвал их «электрическими» (
Электрический заряд — физическая скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел (частиц).
Электрический заряд, как и масса, не существует без тела или частицы, а заряд любой системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему.
Существуют два вида электрических зарядов, которые условились называть положительными и отрицательными. Причём при взаимодействии одноимённо заряженные тела (частицы) отталкивают друг друга (рис. 95, а), а разноимённо заряженные — притягивают друг друга (рис. 95, б).
Заряды разных тел (частиц) могут отличаться не только знаками, но и числовыми значениями.
За единицу электрического заряда в СИ принят кулон (Кл). Эта единица названа в честь Шарля Кулона (1736—1806). 1 Кл — величина электрического заряда, проходящего через поперечное сечение проводника за промежуток времени 1 с при силе постоянного тока 1 А.
Интересно знать:
Один кулон — очень большая величина заряда. Расчёты показывают, что на удалённом от всех остальных тел металлическом шаре, находящемся в сухом воздухе, может находиться избыточный заряд 1 Кл, если его диаметр не менее 110 м. Вместе с тем при включении автомобильных фар сила тока в цепи приблизительно 10 А, т. е. ежесекундно через поперечное сечение проводников, подсоединённых к фарам, проходит заряд приблизительно 10 Кл.
На рубеже XIX и XX столетий учёные экспериментально установили, что в природе существует электрический заряд, модуль которого минимален. Этот заряд назвали элементарным. Вы знаете, что ядра всех атомов содержат протоны, которые являются носителями положительного элементарного заряда, а сами атомы содержат электроны, являющиеся носителями отрицательного элементарного заряда. Учёные с точностью порядка 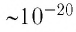
Модуль элементарного электрического заряда 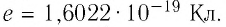
Электроны, протоны и нейтроны входят в состав всех тел, так как из них состоят атомы и молекулы любого вещества*. В электрически нейтральном теле алгебраическая сумма зарядов всех частиц равна нулю. Если каким-нибудь образом создать в таком теле избыток зарядов одного знака, то оно окажется заряженным. Заряд тела 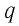
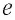
где 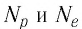
Например, тело, заряд которого 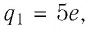
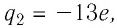
Интересно знать:
В одном моле вещества ( 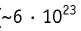
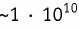
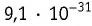
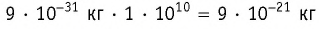
Закон сохранения электрического заряда:
Вы знаете, что при трении соприкасающиеся тела электризуются, при этом модули противоположных по знаку зарядов, возникших на телах, равны. Проверим это на опыте. Наэлектризуем трением соприкасающиеся друг с другом эбонитовую палочку и кусочек меха пли шерстяной ткани.
Поместим поочерёдно внутрь металлической сферы, укреплённой на стержне электрометра, эбонитовую палочку (рис. 96, а) и кусочек меха (рис. 96, б). Стрелка электрометра отклонится, причём, как в первом, так и во втором случаях, на одинаковые углы. Если же одновременно опустить внутрь сферы эбонитовую палочку и кусочек меха (рис. 96, в), то стрелка электрометра останется на месте. Следовательно, модули зарядов обоих тел равны, а их знаки противоположны.
* Исключением является водород, у которого ядра атомов — протоны.
Результаты многочисленных экспериментов позволили сформулировать утверждение, которое является фундаментальным законом природы — законом сохранения электрического заряда: в электрически изолированной системе при любых взаимодействиях алгебраическая сумма электрических зарядов остаётся постоянной:
где 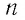
Принято считать систему тел (частиц) электрически изолированной, если между ней и внешними телами нет обмена электрически заряженными частицами.
Закон сохранения электрического заряда указывает на важную особенность электрических явлений: электрические заряды всегда появляются парами. Так, например, при электризации трением тела приобретают заряды противоположных знаков, модули которых одинаковые.
Из истории физики:
Закон сохранения электрического заряда впервые был сформулирован и экспериментально подтверждён М. Фарадеем в 1843 г.
Взаимодействие точечных зарядов и закон Кулона
Электрически заряженные тела (частицы) взаимодействуют друг с другом. Но как определить силу, которой одно заряженное тело притягивает или отталкивает другое?
Вы уже встречались с физическими моделями при изучении механики (материальная точка) и молекулярной физики (идеальный газ). В электростатике при изучении взаимодействия электрически заряженных тел эффективной оказывается модель «точечный заряд».
Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
Вспомните, закон всемирного тяготения также сформулирован для точечных тел (материальных точек).
Закон Кулона. Кулон детально исследовал взаимодействие неподвижных точечных зарядов. Он на опыте изучил зависимость сил электрического взаимодействия тел от модулей зарядов этих тел и расстояния между ними.
В своих опытах Кулон использовал специальный прибор — крутильные весы (рис. 98). Крутильные весы представляют собой два стеклянных цилиндра, внутри которых на тонкой серебряной нити подвешено лёгкое непроводящее коромысло. На одном конце коромысла закреплён проводящий шар 1, а на другом — бумажный противовес 3. Шар 1 можно заряжать с помощью такого же проводящего шара 2. Он находится на изолирующем стержне, закреплённом на крышке нижнего цилиндра. При соприкосновении шара 1 с заряженным шаром 2 заряд распределяется между ними поровну, и шары отталкиваются. По углу закручивания нити, отсчитываемому но шкале прибора, можно определить силу взаимодействия заряженных шаров.
Проведя большое количество опытов, Кулон установил, что модуль сил взаимодействия двух заряженных шаров 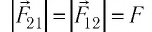
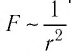
Обобщив экспериментальные данные, Кулон сформулировал закон, получивший его имя.
Закон Кулона: модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела:
где 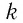
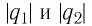
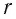
В СИ коэффициент пропорциональности
где 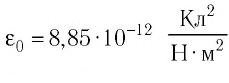
Силы 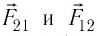
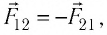
Взаимодействие системы точечных зарядов
Экспериментально установили, что силы взаимодействия двух точечных зарядов не изменяются при появлении третьего точечного заряда или любого числа точечных зарядов. В этом случае силы воздействия 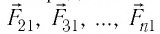
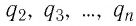
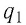
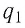
Используя принцип суперпозиции и закон Кулона, можно описать электростатическое взаимодействие любой системы точечных зарядов. На рисунке 100 представлены три взаимодействующих между собой точечных электрических заряда: 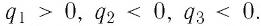
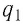
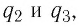
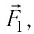
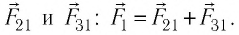
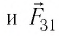
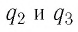
Интересно знать:
Понятие электрического заряда в некоторой степени сходно с понятием гравитационной массы. Электрический заряд определяет интенсивность электромагнитных взаимодействий, а масса — гравитационных. Закон Кулона, описывающий электростатическое взаимодействие, формально похож на закон всемирного тяготения Ньютона, определяющий силы гравитационного взаимодействия:
В обоих случаях модуль сил взаимодействия:
- — обратно пропорционален квадрату расстояния между материальными точками;
- — прямо пропорционален величинам, характеризующим те свойства тел (материальных точек), которые определяют взаимодействия, — массам в одном случае и электрическим зарядам — в другом.
Для измерения сил электрического отталкивания (Ш. Кулон, 1785 г.) и гравитационной постоянной (Г. Кавендиш, 1788 г.) учёные использовали похожие по устройству экспериментальные установки.
Однако между силами гравитационного и электростатического взаимодействий существует и важное различие. Ньютоновские силы тяготения — это всегда силы притяжения. Кулоновские же силы взаимодействия зарядов могут быть как силами притяжения (между разноимёнными зарядами), так и силами отталкивания (между одноимёнными зарядами).
Диэлектрическая проницаемость вещества
Из опытов следует, что взаимодействие электрически заряженных тел в воздухе практически не отличается от их взаимодействия в вакууме. Если заряженные тела находятся в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил их взаимодействия оказывается меньше, чем в вакууме. Чтобы учесть влияние среды, ввели её специальную характеристику, называемую диэлектрической проницаемостью.
Диэлектрическая проницаемость вещества — физическая величина, показывающая, во сколько раз модуль сил электростатического взаимодействия зарядов в данной однородной среде меньше модуля сил взаимодействия этих же зарядов в вакууме:
где 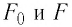
С учётом соотношения (17.2) закон Кулона можно записать следующим образом:
Диэлектрическая проницаемость вакуума равна 1. За 1 принимают и диэлектрическую проницаемость воздуха, поскольку её значение (при нормальном атмосферном давлении) 1,0006. Диэлектрические проницаемости других однородных сред всегда больше единицы. Например, у воды диэлектрическая проницаемость 81, у глицерина — 56, а у керосина — 2.
Интересно знать:
Диэлектрическая проницаемость дистиллированной воды при температуре 25°С равна 78,54, а при температуре 0°С — 88. Обычно без указания температуры диэлектрическую проницаемость воды полагают равной 81.
Пример №1
Два точечных заряда находятся в керосине на расстоянии 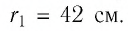
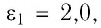
Решение. Поскольку 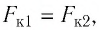
Следовательно, 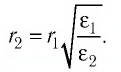
Ответ:
Пример №2
Точечные заряды 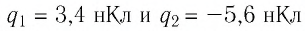
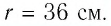
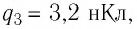
Решение. Изобразим на рисунке силы 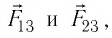
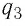
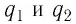
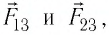
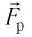
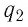
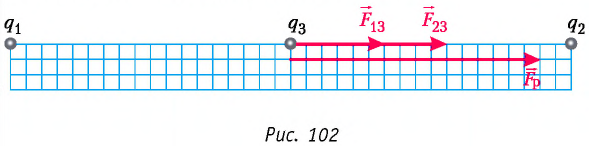
Поскольку силы 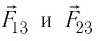
Ответ: 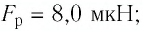
Видео:Вектор потенциал. ЭлектродинамикаСкачать

Электростатическое поле
Заряженные тела и частицы, которые кратко называют зарядами, взаимодействуют друг с другом. Это подтверждают многочисленные опыты, а закон Кулона позволяет определить силы взаимодействия неподвижных точечных зарядов. Но что является причиной подобного взаимодействия, каков его механизм?
Первым, кто догадался, что «тела действуют друг на друга на расстоянии посредством обращения окружающей среды в состояние напряжения», был выдающийся английский учёный Майкл Фарадей (1791 — 1867). Обобщая результаты собственных исследований, проведённых с 1832 по 1852 г., Фарадей ввёл в физику новое понятие — поле. Он рассматривал поле как материальную среду, которая является посредником при любых взаимодействиях удалённых друг от друга тел.
По современным представлениям, электрический заряд наделяет окружающее пространство особыми физическими свойствами — создаёт электрическое поле. Этот заряд называют источником поля и часто обозначают символом Q. Основным свойством электрического поля является его действие некоторой силой на внесённый в него заряд. Иначе говоря, заряды не действуют друг на друга непосредственно. Взаимодействие электрических зарядов осуществляется посредством создаваемых ими полей.
Так, например, при взаимодействии неподвижных электрических зарядов электростатическое поле заряда 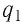
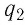
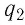
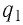
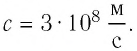
Электростатическое поле — поле, создаваемое неподвижными относительно используемой инерциальной системы отсчёта электрическими зарядами.
Электростатическое поле существует в пространстве, окружающем неподвижные заряды, неразрывно с ними связано и не изменяется со временем. Силу, которой поле действует на вносимый в него электрический заряд, называют электрической силой или кулоновской силой.
Чтобы исследовать электростатическое поле, создаваемое зарядом 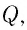
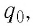
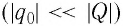
Отметим, что свойство электрического поля воздействовать некоторой силой проявляется не только в точке, в которой находится пробный заряд 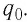
Используя пробный заряд 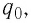
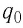
Из истории физики:
По мнению А. Эйнштейна, идея поля была самым важным открытием со времён Ньютона. Он писал, что «надо иметь могучий дар научного предвидения, чтобы распознать, что в описании электрических явлений не заряды и не частицы описывают суть явлений, а скорее пространство между зарядами и частицами». Фарадей создал концепцию электромагнитного поля, основанную на конечной скорости распространения любых взаимодействий. Математическую завершённость идее Фарадея придал его гениальный соотечественник и преемник Джеймс Клерк Максвелл (1831-1879).
Напряжённость электростатического поля. Принцип суперпозиции
Для изучения свойств электростатического поля удобно использовать такую его характеристику, которая не зависит от числового значения пробного заряда и позволяет определить силу, действующую на заряд со стороны поля в любой его точке. Для гравитационного поля такой характеристикой, не зависящей от массы тела, является ускорение свободного падения 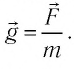
Напряжённость электростатического поля:
Пусть электростатическое поле создано в вакууме точечным зарядом 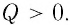
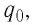
Сила 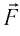
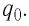
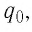
и, следовательно, может служить характеристикой поля.
Эту характеристику называют напряжённостью электростатического поля и обозначают 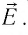
Напряжённость электростатического поля — физическая векторная величина, равная отношению силы, которой поле действует на пробный заряд, к значению этого заряда:
С учётом выражений (19.1) и (19.2) можно определить модуль напряжённости электростатического поля, созданного точечным зарядом 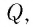
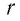
Таким образом, модуль напряжённости поля, создаваемого в вакууме точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости.
Если заряд Q находится в однородной среде с диэлектрической проницаемостью 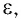
Из выражения 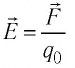
В СИ широко используют другое название этой единицы — вольт на метр
Зная напряжённость электростатического поля, можно определить силу, действующую на любой точечный заряд в любой точке этого поля:

Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля точечного заряда направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле.
Напряжённость поля, созданного точечным положительным зарядом 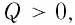
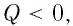
Интересно знать:
Кроме гравитационного поля у Земли есть электрическое и магнитное поля. Модуль напряжённости электрического поля у поверхности Земли в среднем составляет 130 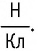
Принцип суперпозиции электрических полей:
Пусть пробный заряд 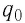
Воспользовавшись формулой (19.3), можно определить силы, действующие на пробный заряд:
где 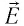
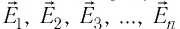
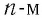
Подставив эти выражения в соотношение (19.4), получим, что если в данной точке пространства электростатическое поле создано системой точечных зарядов, то напряжённость результирующего поля в этой точке равна векторной сумме напряжённостей полей, создаваемых каждым из точечных зарядов системы в отдельности:
Это положение называют принципом суперпозиции полей.
Воспользуемся принципом суперпозиции, чтобы определить в точках А и В напряжённости результирующего поля, созданного двумя точечными электрическими зарядами противоположных знаков 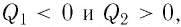
Напряжённости 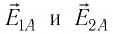
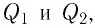
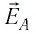
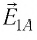
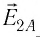
Напряжённость 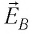
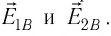
Пример №3
Два неподвижных точечных заряда 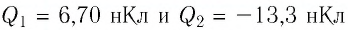
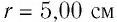
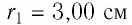
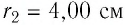
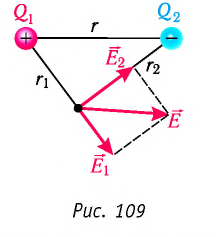
Решение. Согласно принципу суперпозиции, напряжённость результирующего поля 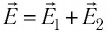
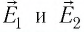
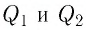
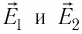
Модуль напряжённости Е результирующего поля найдём
по теореме Пифагора: 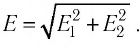
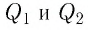
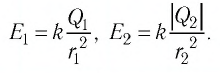
С учётом этого
Ответ:
Линии напряжённости электростатического поля
Для описания электростатического поля нужно знать как модуль, так и направление напряжённости в каждой его точке. Чтобы наглядно отображать распределение поля в пространстве, Фарадей в 1845 г. предложил способ изображения электрических полей в виде воображаемых линий. Их назвали линиями напряжённости или силовыми линиями.
Линии напряжённости — воображаемые направленные линии, касательные к которым в каждой точке поля совпадают по направлению с напряжённостью электростатического поля в тон же точке (т.е. с направлением электростатической силы, действующей на положительный заряд) (рис. 111).
Очевидно, что через любую точку поля, в которой 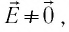
На рисунке 112, а изображены линии напряжённости полей, образованных зарядами, равномерно распределёнными по поверхности уединённых проводящих шариков. Направление каждой стрелки на рисунке 112, а совпадает с направлением напряжённости поля. Линии напряжённости в первом случае направлены от положительного заряда в бесконечность, а во втором — из бесконечности к отрицательному заряду и оканчиваются на нём. В электростатическом поле линии напряжённости начинаются и оканчиваются на электрических зарядах даже тогда, когда одним своим концом уходят в бесконечность, где и находятся недостающие на рисунке заряды.
На рисунке 112, б изображены линии напряжённости электростатического поля, образованного двумя разноимёнными зарядами, модули которых одинаковые, находящимися на проводящих шариках. Стрелки показывают направления напряжённости поля в различных его точках.
На рисунке 112, в представлены линии напряжённости электростатического поля двух одинаково заряженных шариков.
На рисунке 112, г изображено поле, созданное зарядами противоположных знаков, модули которых одинаковые, находящимися на двух плоских металлических пластинах, длина которых много больше расстояния между ними. Линии напряжённости такого поля параллельны друг другу за исключением пространства вблизи краёв пластин и вне области их перекрытия. Электростатическое поле в центральной области между разноимённо заряженными металлическими пластинами является примером однородного поля.
Однородное электростатическое поле — электростатическое поле, напряжённость которого во всех точках пространства одинакова.
Электростатические поля, изображённые на рисунках 112, а, б, в, являются неоднородными, так как или модуль, или направление (или и то, и другое) напряжённости в разных точках поля отличается.
Линии напряжённости электростатического поля не прерываются в пространстве (при отсутствии в нём других зарядов), никогда не пересекаются и не касаются друг друга.
Чтобы линии напряжённости отображали не только направление, но и модуль напряжённости поля, на рисунках их условились проводить с определённой густотой. Линии напряжённости идут гуще там, где модуль напряжённости поля больше, и реже там, где он меньше. В однородном электростатическом поле густота линий напряжённости не меняется. Картину линий напряжённости принято строить так, чтобы она, по возможности, отображала симметрию изображаемого электростатического поля. Число линий напряжённости, началом или концом которых служит данный заряд, пропорционально значению этого заряда (рис. 113).
Работа силы однородного электростатического поля
Электростатическое поле, действуя на находящиеся в нём заряды с определённой силой, может их перемещать. Вы знаете, что при перемещении тела действующая на него сила совершает работу. Выясним, от чего зависит работа силы по перемещению электрического заряда в электростатическом поле.
Расчёты и результаты экспериментов доказали, что работа силы электростатического поля при перемещении заряда между двумя точками зависит только от положения этих точек и не зависит от вида траектории. Такой же особенностью, как вы знаете, обладает и гравитационное поле. Физические поля, работа сил которых не зависит от формы траектории, называют потенциальными.
Выясним, как можно определить работу силы однородного электростатического поля напряжённостью 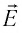
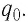
Вам известно, что работа силы 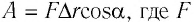
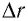
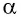
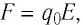
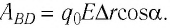
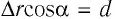
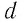
Работа силы электростатического поля может быть положительной, отрицательной или равной нулю. Например, если бы заряд перемещался не из точки В в точку D, а наоборот — из точки D в точку В, то работа силы была бы отрицательной: 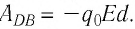
Потенциальная энергия заряда в электростатическом поле
Электростатическое поле является потенциальным, и, следовательно, работа силы поля по перемещению электрического заряда 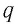
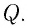
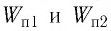
где 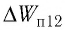
Перепишем выражение (21.2) в виде
и проанализируем его, когда на заряд q действует только сила со стороны электростатического поля:
1) если работа силы поля 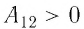
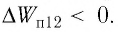
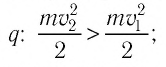
2) если работа силы поля 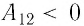
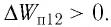
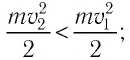
3) если работа силы поля 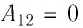
Потенциал электростатического поля как его энергетическая характеристика.
Из выражений (21.1) и (21.2) следует, что потенциальная энергия пробного заряда 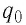
Следовательно, отношение 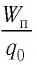
Потенциал электростатического поля в данной точке пространства — физическая скалярная величина, равная отношению потенциальной энергии пробного заряда, помещённого в данную точку ноля, к значению этого заряда:
За единицу потенциала в СИ принят вольт (В). Единица названа в честь итальянского учёного Алессандро Вольта (1745—1827), внёсшего большой вклад в изучение электрических явлений. 1 В — потенциал такой точки электростатического поля, в которой заряд 1 Кл обладал бы потенциальной энергией 1 Дж.
Потенциал 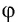
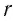
Знак заряда-источника поля определяет знак потенциала этого поля.
Если электрическое поле создано в однородной среде с диэлектрической проницаемостью 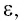
Потенциал является скалярной величиной. Поэтому, если в данной точке пространства электростатическое поле создано системой точечных зарядов, то потенциал результирующего поля в этой точке равен алгебраической сумме потенциалов полей в этой же точке пространства, создаваемых каждым из точечных зарядов системы в отдельности:
т. е. для потенциала выполняется принцип суперпозиции.
Пример №4
Электростатическое поле создано неподвижным точечным зарядом Q. В точке, находящейся на расстоянии 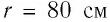
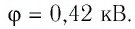
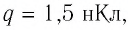
Решение. Модуль силы, которой электростатическое поле заряда Q действует на заряд 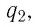
Из формулы (21.5) для потенциала поля точечного заряда найдём значение заряда:
Подставив выражение (2) в формулу (1), получим:
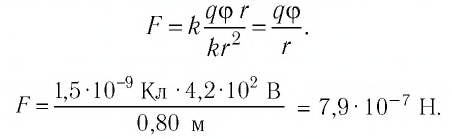
Ответ:
Разность потенциалов электростатического поля
Связь между напряжением и напряжённостью однородного электростатического поля:
Потенциальная энергия любой системы тел, взаимодействующих посредством потенциальных сил, зависит от выбора нулевой точки (нулевого уровня). Однако изменение потенциальной энергии однозначно характеризует процесс перехода системы из одного состояния в другое. Это относится и к изменению потенциальной энергии заряженной частицы (заряда) в электростатическом поле.
Перемещение заряженных частиц в электростатическом поле, сопровождаемое изменением их потенциальной энергии, характеризуют, используя понятие «разность потенциалов». Как и приращение потенциальной энергии, разность потенциалов не зависит от выбора нулевой точки. Пусть пробный заряд 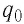
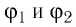
Разность потенциалов 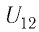
С учётом выражений (21.3) и (21.4) получим:
Из выражения (22.1) следует, что разность потенциалов численно равна убыли потенциальной энергии перемещаемого в поле единичного пробного заряда.
Противоположную по знаку разности потенциалов величину называют приращением потенциала
За единицу разности потенциалов в СИ принимают вольт (В). 1 В — разность потенциалов 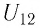
Отметим, что когда говорят о «потенциале поля в некоторой точке», под этим всегда понимают разность потенциалов между этой точкой и точкой, потенциал поля в которой приняли равным нулю.
Потенциал проводника можно измерить электрометром. Для этого проводник соединяют со стрелкой электрометра, корпус которого заземляют. Отклонение стрелки электрометра покажет наличие разности потенциалов между проводником и Землёй. Приняв потенциал Земли равным нулю, можно считать, что электрометр измеряет потенциал проводника.
Если имеются два заряженных проводника, то, соединив один из них со стрелкой, а другой — с корпусом электрометра, измеряют разность потенциалов между заряженными проводниками.
Связь между напряжением и напряжённостью однородного электростатического поля. Термин «напряжение» ввёл в 1792 г. Вольта. Отметим, что для электростатических полей понятия «электрическое напряжение» и «разность потенциалов» тождественны.
Работа, совершаемая силой однородного электростатического поля напряжённостью 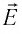
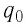
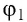
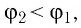
а в соответствии с выражением (21.1)
где 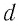
Приравнивая соответствующие части равенств, найдём выражение, устанавливающее связь между модулем напряжённости однородного электростатического поля и разностью потенциалов, т. е. между двумя характеристиками электростатического поля: 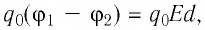
Из выражения (22.2) следует: чем больше разность потенциалов между двумя точками однородного электростатического поля, тем больше модуль напряжённости поля. Если разность потенциалов равна нулю (потенциал поля не меняется), то модуль напряжённости поля также равен нулю.
Принимая во внимание, что 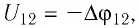
На основании формулы (22.3) вводят единицу напряжённости СИ вольт на метр 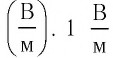
Используя термин «напряжение», на практике точки 1 и 2 поля выбирают так, чтобы
Пример №5
Электростатическое поле создано точечным зарядом 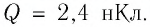
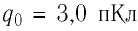
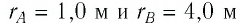
Решение. Поле электростатическое, поэтому работа силы поля при переносе пробного заряда 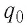
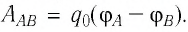
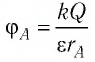
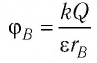
Тогда
Подставив числовые значения, получим
Ответ:
Пример №6
Электрон начинает двигаться в электрическом поле от точки 1 до точки 2. Определите модуль скорости движения электрона в точке 2, если он ускоряется разностью потенциалов 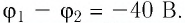
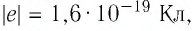
Решение. Сила электрического поля совершает работу по изменению кинетической энергии электрона: 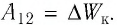
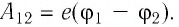
Изменение кинетической энергии электрона
Тогда с учётом формулы (1) модуль скорости движения электрона в точке 2:
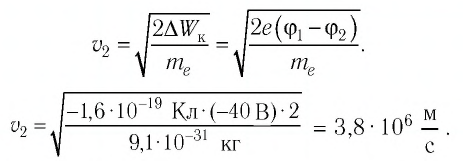
Ответ:
Конденсаторы
Во многих электротехнических и радиотехнических приборах используют устройства, способные при малых размерах накапливать значительные разноимённые электрические заряды и связанную с ними электрическую энергию. Какие это устройства и от чего зависят накопленные ими заряды и запасённая энергия?
Для накапливания значительных разноимённых зарядов используют устройство, называемое конденсатором (от лат. condensator, буквально — тот, кто уплотняет, сгущает). Простейший конденсатор — система, состоящая из двух проводников, разделённых слоем диэлектрика, толщина d которого мала по сравнению с размерами проводников (рис. 119). Проводники, образующие конденсатор, называют его обкладками.
На обкладках конденсатора накапливаются противоположные по знаку электрические заряды, модули которых равны. 11роцесс накапливания зарядов на обкладках называют зарядкой конденсатора, а процесс нейтрализации зарядов при соединении обкладок конденсатора проводником — разрядкой конденсатора. Модуль заряда, находящегося на одной из обкладок конденсатора, называют зарядом конденсатора.
Из истории физики:
В 1745—1746 гг. немецкий физик Эвальд фон Клейст (1700—1748) и нидерландский физик Питер ван Мушенбрук (1692—1761) независимо друг от друга изобрели первый конденсатор — лейденскую банку. Изобретение конденсатора способствовало изучению электрических явлений, так как позволило накапливать большие электрические заряды.
Интересно знать:
Широко распространённый тип конденсаторов представляют собой две ленты металлической фольги, разделённые тонкой парафинированной бумагой, полистиролом, слюдой или другим диэлектриком, которые свёрнуты в тугой рулон и запаяны (рис. 120). Используют и так называемые воздушные конденсаторы, в которых изолирующим слоем, отделяющим проводники, является воздух.
Электроёмкость конденсатора
В процессе зарядки простейшего конденсатора его обкладки приобретают противоположные по знаку заряды 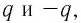
Следовательно, величина, равная отношению 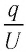
Электрическая ёмкость конденсатора — физическая скалярная величина, равная отношению заряда конденсатора к напряжению между его обкладками:
Проанализировав формулу (23.1), можно сделать вывод: чем меньше напряжение 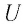
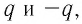
Единицей электрической ёмкости в СИ является фарад (Ф).
1 Ф — очень большая электроёмкость. Электроёмкостью 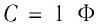
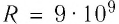
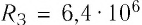
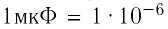
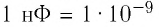
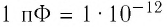
Например, электроёмкость такого огромного проводника, как земной шар, равна 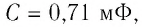
Из истории физики:
В XVII—XVIII вв. учёные рассматривали электричество как «нематериальную жидкость». Эта «жидкость» могла «вливаться» в проводник и «выливаться» из него. Так появился термин «электрическая ёмкость».
Интересно знать:
На схемах номинальную электроёмкость конденсаторов обычно указывают в микрофарадах и пикофарадах. Однако реальная электроёмкость конденсатора может значительно меняться в зависимости от многих факторов. Другой, не менее важной, характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором его можно использовать в заданных условиях в течение срока службы. Это напряжение может находиться в пределах от нескольких вольт до нескольких сотен киловольт. Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. Для многих типов конденсаторов с увеличением температуры допустимое напряжение уменьшается.
Электроёмкость плоского конденсатора
Если обкладками конденсатора являются две одинаковые параллельные друг другу пластины, то конденсатор называют плоским. Электростатическое поле заряженного плоского конденсатора в основном сосредоточено между его обкладками и является практически однородным. Вблизи краёв пластин однородность поля нарушается, однако этим часто пренебрегают, когда расстояние между пластинами значительно меньше их размеров (рис. 121).
Чтобы установить, от чего зависит электроёмкость плоского конденсатора, проведём несколько опытов. В качестве обкладок конденсатора используем две металлические пластины, расположенные в воздухе на некотором расстоянии параллельно друг другу. Соединим стержень электрометра с одной из пластин, а его корпус с другой (рис. 122). Зарядим конденсатор, подключив его к источнику тока на некоторый промежуток времени. Когда между пластинами конденсатора возникнет напряжение (стрелка электрометра отклонится), отключим его от источника тока.
Если перемешать пластины относительно друг друга, уменьшая площадь их взаимного перекрытия при неизменном расстоянии между ними, то показания электрометра при этом увеличиваются, хотя сообщённый пластинам при зарядке конденсатора заряд не изменяется. Так как напряжение между пластинами увеличивается при уменьшении площади перекрытия пластин конденсатора, то его электроёмкость должна уменьшаться
Увеличивая расстояние между пластинами конденсатора, не меняя площади их перекрытия, будем наблюдать возрастание показаний электрометра, т. е. увеличение напряжения между пластинами конденсатора, что возможно при уменьшении его электроёмкости. Значит, чем больше расстояние между пластинами конденсатора, тем меньше его электроёмкость
Если между обкладками конденсатора поместить пластину из диэлектрика, например из стекла, то показания электрометра уменьшатся. Напряжение между обкладками в этом случае уменьшается, следовательно, электроёмкость конденсатора увеличивается
В СИ коэффициентом пропорциональности между электроёмкостью конденсатора и определяющими её величинами 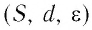
Результаты экспериментов позволяют записать формулу для определения электроёмкости плоского конденсатора:
где 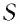
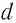
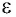
Условное изображение конденсатора постоянной электроёмкости на электрических схемах представлено на рисунке 123.
Интересно знать:
Зависимость электроёмкости конденсатора от расстояния между его обкладками используют в схемах кодирования клавиатуры персонального компьютера. Под каждой клавишей находится конденсатор, электроёмкость которого изменяется при нажатии на клавишу. Микросхема, подключённая к каждой клавише, при изменении электроёмкости выдаёт кодированный сигнал, соответствующий данной букве (рис. 124).
Пример №7
Плоскому конденсатору электроёмкостью 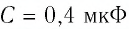
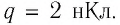
Решение. Модуль напряжённости однородного электростатического поля определим по формуле 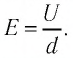
Ответ:
Пример №8
Пространство между обкладками плоского конденсатора заполнено диэлектриком. Конденсатор зарядили до напряжения 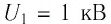
Решение. В обоих случаях заряд конденсатора будет одинаковым 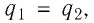
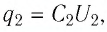
Электроёмкость плоского конденсатора определяют по формуле
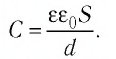
Для рассматриваемых случаев электроёмкости соответственно равны:
Подставив формулы (2) в равенство (1), получим:
Ответ:
Энергия электростатического поля конденсатора
Процесс зарядки конденсатора можно представить как перенос заряда 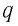
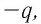
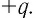
Убедиться в том, что заряженный конденсатор обладает энергией, можно на опыте. Соберём электрическую цепь, состоящую из источника тока, конденсатора и электрической лампы. Схема цепи представлена на рисунке 125. Зарядим конденсатор, подсоединив его к источнику тока. Затем, отключив конденсатор от источника тока, подсоединим его к лампе. При этом наблюдаем кратковременную вспышку света. В данном случае во время разрядки конденсатора энергия, запасённая им при зарядке, превращается во внутреннюю энергию спирали лампы, часть этой энергии расходуется на излучение света. При прохождении электрического тока по цепи с источником тока конденсатор заряжался, т. е. на его обкладках накапливались электрические заряды. При этом в окружающем конденсатор пространстве возникло электростатическое поле. Суммарный электрический заряд обеих обкладок конденсатора до его зарядки, во время зарядки и после разрядки конденсатора равен нулю. Единственное изменение, которое произошло при разрядке конденсатора, заключается в том, что исчезло электростатическое поле, которое создавалось зарядами обеих обкладок конденсатора. Следовательно, энергией обладало электростатическое поле, образованное зарядами обкладок заряженного конденсатора.
Расчёты подтверждают, что формулу для определения энергии электростатического поля заряженного конденсатора можно записать в виде:
Применение конденсаторов
Конденсаторы находят широкое применение в электротехнике, радиотехнической и телевизионной аппаратуре, радиолокационной технике, телефонии, технике счётно-решающих устройств, лазерной технике, электроэнергетике (например, для улучшения коэффициента мощности промышленных установок, регулирования напряжения в распределительных сетях, в устройствах освещения люминесцентными лампами), металлопромышленности (например, для плавки и термической обработки металлов), добывающей промышленности (например, в электровзрывных устройствах), медицинской технике (например, в рентгеновской аппаратуре, приборах электротерапии), фототехнике (для получения вспышки света при фотографировании).
В связи с этим наряду с миниатюрными конденсаторами (рис. 126, а), имеющими массу менее грамма и размеры порядка нескольких миллиметров, существуют конденсаторы с массой в несколько тонн (рис. 126, б).
Пример №9
Определите, как и во сколько раз изменится энергия электростатического поля заряженного плоского воздушного конденсатора, если пространство между его обкладками заполнить керосином, диэлектрическая проницаемость которого 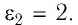
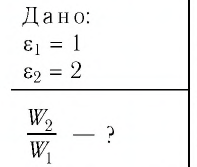
Решение. Электроёмкость воздушного конденсатора 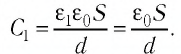
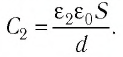
В случае а) конденсатор отключён от источника тока, поэтому 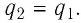
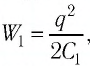
Таким образом, энергия электростатического поля уменьшилась в 2 раза. В случае б) конденсатор не отключён от источника тока, поэтому напряжение между его обкладками равно напряжению между полюсами источника тока 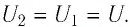
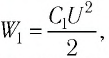
Таким образом, энергия электростатического поля увеличилась в 2 раза.
Ответ: а) энергия электростатического поля уменьшилась в 2 раза; б) энергия электростатического поля увеличилась в 2 раза.
Пример №10
Плоский воздушный конденсатор, площадь перекрытия обкладок которого 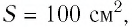
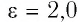
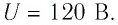
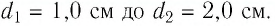
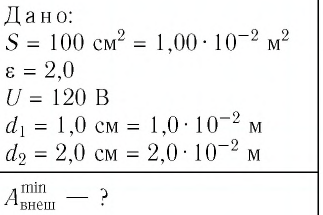
Решение. Модуль заряда каждой из обкладок конденсатора
Энергия электростатического поля конденсатора до изменения расстояния между его обкладками
После отключения конденсатора от источника тока заряды на его обкладках не изменяются.
Энергию электростатического поля конденсатора после увеличения расстояния между его пластинами определим следующим образом:
Минимальная работа, которую необходимо совершить внешней силе, чтобы увеличить расстояние между обкладками конденсатора, равна приращению энергии электростатического поля конденсатора, так как при медленном увеличении расстояния между обкладками конденсатора их кинетическая энергия остаётся близкой нулю.
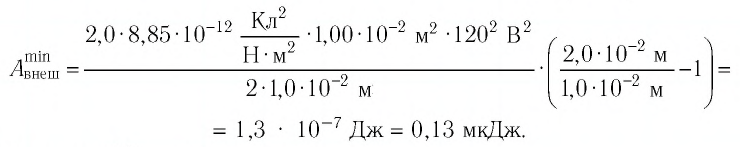
Ответ:
Обобщение и систематизация знаний:
Видео:1.2 Материальные уравнения, векторы поляризованности и намагниченности средСкачать

Постоянный электрический ток
Постоянный ток — модель электрического тока, в которой сила тока не зависит от времени при неизменном распределении заряда в проводнике.
Термин «электрический ток» и определение направления тока введены Андре-Мари Ампером в 1820 г.
Электрический ток — направленное (упорядоченное) движение заряженных частиц — носителей заряда.
- Сила тока — физическая скалярная величина, равная отношению заряда, прошедшего через поперечное сечение проводника за некоторый промежуток времени, к этому промежутку времени.
- За направление электрического тока условно принято направление упорядоченного движения положительно заряженных частиц.
- Сила тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению:
(Закон Ома для участка электрической цепи.)
Сопротивление проводника прямо пропорционально длине и обратно пропорционально площади поперечного сечения:
Соединение проводников 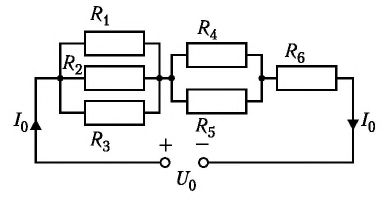
последовательное параллельное
Вы научились собирать электрические цепи и знаете, что обязательными их звеньями являются источник тока и потребитель. Источник тока обеспечивает требуемое напряжение на потребителе — устройстве, в котором необходимо создать электрический ток и использовать какие-то из его действий: тепловое, химическое, магнитное, световое. В данной главе мы рассмотрим условия существования тока и процессы, происходящие в электрической цепи, введём характеристики источника тока. Это стало возможным после изучения характеристик электростатического поля.
Условия существования постоянного электрического тока
Для возникновения электрического тока необходимо наличие свободных заряженных частиц, способных перемещаться по проводнику под действием силы электрического поля. Такой электрический ток называют током проводимости. Что же обеспечивает существование электрического тока в проводнике в течение длительного промежутка времени?
Для поддержания в проводнике постоянного электрического тока необходимо, чтобы проводник являлся частью замкнутой цепи. Но вы знаете, что работа электростатического поля при перемещении электрического заряда по замкнутому контуру равна пулю. Следовательно, в цепи должен быть участок, на котором осуществляется работа по перемещению заряда против сил электрического поля. Таким участком является источник тока.
Рассмотрим замкнутую электрическую цепь, состоящую из источника тока (участок ас) и металлического проводника (участок abc) (рис. 130).
В проводнике abc свободные электроны под действием сил электрического поля перемещаются от точки с к точке а. Чтобы движение носителей заряда в цепи было продолжительным, электроны от точки а должны перемещаться к точке с. Самопроизвольно такое перемещение электронов происходить не может, так как на них в противоположном направлении (от точки с к точке а) действует сила электрического поля 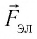
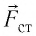
Сторонние силы
Сторонние силы действуют на заряженные частицы только внутри источников тока, совершая работу по разделению положительных и отрицательных зарядов. В результате такого разделения на одном полюсе источников тока накапливаются положительные заряды, а на другом — отрицательные, что приводит к возникновению электрического поля. Это поле, действуя силой на свободные электроны, заставляет их двигаться в электрической цепи вне источника тока. Таким образом, действие электрической силы приводит к соединению разноимённых зарядов и уменьшению разности потенциалов, тогда как действие сторонни -ей силы приводит к разделению разноимённых зарядов и поддержанию разности потенциалов на полюсах источников тока.
В химических источниках тока (гальванических элементах, аккумуляторах) (рис. 131, а) разделение зарядов происходит при химических реакциях, в электромеханических индукционных генераторах (рис. 131, б) — при совершении механической работы, в солнечных батареях (рис. 131, в) — под воздействием энергии солнечного излучения и т. д.
Участок цепи, где заряды движутся под действием только электрической силы, называют внешним (различные потребители электрического тока, соединительные провода, измерительные приборы). Участок цепи, где заряды движутся под действием сторонней и электрической сил, называют внутренним (источник тока).
Электродвижущая сила источника тока
Основной характеристикой источника тока является электродвижущая сила (ЭДС)*. Обозначают её
ЭДС — физическая скалярная величина, равная отношению работы сторонней силы по перемещению положительного электрического заряда внутри источника тока от его отрицательного полюса к положительному к значению этого заряда:
Сравнив формулы 
Таким образом, ЭДС численно равна работе сторонней силы по перемещению единичного заряда внутри источника тока между его полюсами (положительного заряда от отрицательного полюса к положительному, отрицательного заряда, наоборот, от положительного полюса к отрицательному).
* Термин «электродвижущая сила» неудачен, поскольку в данном случае речь не идёт ни о какой силе, измеряемой в ньютонах. Поэтому в дальнейшем мы будем использовать только сокращённое название ЭДС.
Закон Ома для полной электрической цепи
В 1826 г. немецкий физик Георг Симон Ом (1787—1854) опытным путём установил, что при постоянной температуре отношение напряжения между концами металлического проводника к силе тока в нём является величиной постоянной. На основании этого был сформулирован закон, названный законом Ома для участка электрической цепи: 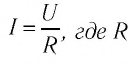
Рассмотрим электрическую цепь, состоящую из источника тока (гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R. Известны ЭДС 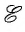
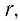
Закон Ома для полной цепи связывает силу тока 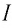
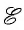
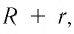
Если через поперечное сечение проводника за промежуток времени 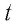
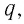
Поскольку сила тока 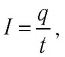
В неподвижных проводниках неизменного химического состава в результате работы сторонних сил происходит увеличение только внутренней энергии внешнего и внутреннего участков цепи. Таким образом, при прохождении электрического тока в резисторе и источнике тока выделяется количество теплоты Q, которое можно определить по закону Джоуля—Ленца:
На основании закона сохранения энергии:
Подставим формулы (26.1) и (26.2) в равенство (26.3) и в результате математических преобразований получим:
Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Поэтому 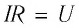
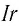
Выражая силу тока из формулы (26.4), получим:
Формула (26.5) является математическим выражением закона Ома для полной электрической цепи, согласно которому сила тока в полной электрической цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи.
Различные режимы работы электрической цепи
Преобразуем формулу (26.4):
так как 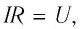
Из выражения (26.6) следует, что при разомкнутой цепи 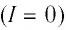
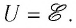
В случае, если сопротивление внешнего участка цепи стремится к нулю 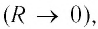
Такой режим работы источника тока называют коротким замыканием, а максимально возможную для данного источника силу тока называют силой тока короткого замыкания:
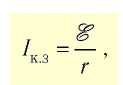
где 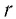
Для источников тока с незначительным внутренним сопротивлением (например, у автомобильных аккумуляторов 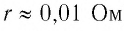
Коэффициент полезного действия источника тока
При перемещении заряда q на внешнем участке цепи, напряжение на котором 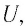
Используя выражение 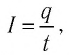
Если внешним участком цепи является нагревательный элемент (или резистор), то с учётом закона Джоуля—Ленца формула для расчёта полезной работы электрического тока на внешнем участке цепи:
Учитывая, что мощность 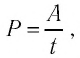
Поскольку работа сторонних сил источника тока:
то мощность, развиваемая сторонними силами источника тока при наличии в цепи только нагревательного элемента:
Следовательно,
Коэффициент полезного действия (КПД) источника тока — отношение полезной мощности тока на внешнем участке цепи к полной мощности, развиваемой сторонними силами источника тока:
Если внешний участок цепи — нагревательный элемент, то
Тогда КПД источника тока
Пример №11
Резистор с сопротивлением 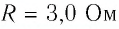
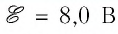
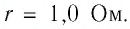
Решение. Полезной является мощность тока на внешнем участке цепи, т. е. на резисторе: 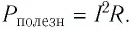
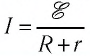
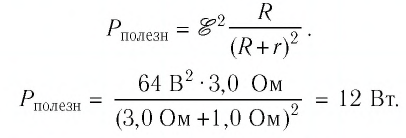
КПД источника тока в данной цепи определим по формуле
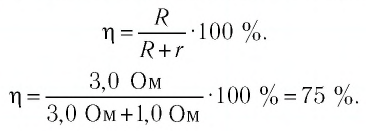
Ответ:
Видео:Экскурсия по классической электродинамикеСкачать

Магнитное поле
Как вы уже знаете, между заряженными телами (частицами), кроме гравитационного, существует и электромагнитное взаимодействие. Если заряды покоятся относительно определённой инерциальной системы отсчёта, электромагнитное взаимодействие между ними называют электростатическим. При движении электрически заряженных тел (частиц) проявляется составляющая электромагнитного взаимодействия — магнитное взаимодействие.
В этой главе вы познакомитесь с явлениями, в которых важную роль играет магнитное взаимодействие, обусловленное существованием магнитного поля, создаваемого постоянными магнитами, электрическим током или изменяющимся во времени электрическим полем.
Действие магнитного поля на проводник с током
Явления взаимодействия одноимённых и разноимённых электрических зарядов напоминают явления отталкивания одноимённых полюсов и притяжения разноимённых полюсов магнитов (рис. 136). Электрические взаимодействия осуществляются посредством электрических полей, а чем обусловлены магнитные взаимодействия и чем определяются магнитные свойства тел?
То, что магниты взаимодействуют друг с другом, что распиленный пополам магнит превращается в два магнита, а железо при соприкосновении с магнитом намагничивается, было установлено достаточно давно. Гораздо позже обнаружили связь между электрическими и магнитными явлениями, хотя намагничивание железных предметов, перемагничивание стрелки компаса во время грозовых электрических разрядов и многие другие наблюдения и опыты заставляли учёных задуматься над этим. Первыми эту связь исследовали в 1820 г. датский физик Ганс Христиан Эрстед (1777—1851) и уже известный вам французский физик и математик Андре-Мари Ампер.
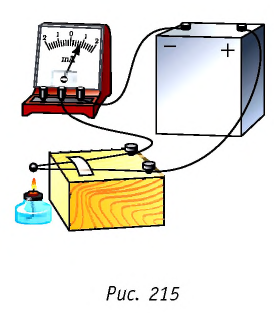
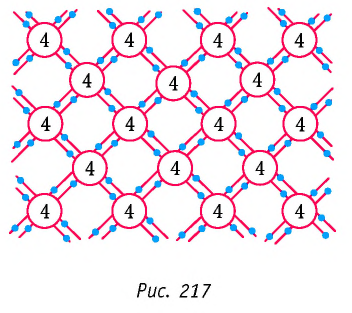
Эрстед обнаружил, что магнитная стрелка, расположенная вблизи проводника, поворачивалась на некоторый угол при прохождении по проводнику электрического тока (рис. 137). Открытие Эрстеда позволило Амперу сделать вывод, что магнитные свойства любого тела определяются замкнутыми электрическими токами, циркулирующими внутри этого тела и получившими название «амперовы токи» или «молекулярные токи» (рис. 138). Это означало, что магнитное взаимодействие обусловлено не особыми магнитными зарядами, а движением электрических зарядов — электрическим током.
Взаимодействие проводника с током и магнитной стрелки в опыте Эрстеда является взаимодействием электрического тока проводника с «амперовыми токами» в магнитной стрелке (гипотеза Ампера). Это взаимодействие осуществляется посредством магнитного поля.
Магнитное поле — особая форма материи, создаваемая движущимися относительно определённой инерциальной системы отсчёта электрическими зарядами или переменными электрическими полями.
Опыты свидетельствуют, что магнитное поле возникает при движении любых электрических зарядов.
Посредством магнитного поля осуществляется взаимодействие между подвижными электрическими зарядами (а также магнитами). При этом каждый движущийся в данной инерциальной системе отсчёта электрический заряд создаёт в окружающем пространстве магнитное поле. Это поле действует некоторыми силами на любые другие движущиеся электрические заряды, а также находящиеся в нём магниты.
Таким образом, о существовании магнитного поля можно судить по наличию силы, действующей на электрический заряд, движущийся относительно выбранной инерциальной системы отсчёта, или находящийся в этом поле магнит.
Интересно знать:
Современные научные представления не отвергают, а наоборот, предсказывают частицы с магнитным зарядом — магнитные монополи. Однако такие частицы пока экспериментально не наблюдали.
Действие магнитного поля на проводник с током:
Поскольку магнитное поле проводника с током действует определённой силой на магнит (в опыте Эрстеда — на магнитную стрелку), то естественно предположить, что со стороны магнитного поля магнита на проводник с током должна действовать сила. Это предположение можно проверить экспериментально.
Соберём электрическую цепь, представленную на рисунке 139, а. При разомкнутой цепи действия со стороны магнитного поля подковообразного магнита на гибкий проводник не наблюдается. При замыкании цепи проводник приходит в движение: он либо втягивается в пространство между полюсами подковообразного магнита (рис. 139, б), либо выталкивается из него (рис. 139, в) при противоположном расположении полюсов магнита (или при изменении направления тока). Этот опыт наглядно доказывает, что магнитное поле действует только на движущиеся заряды.
Во всех рассмотренных случаях на проводники с током (движущиеся заряженные частицы) действовали магнитные силы, которые можно рассматривать как результат взаимодействия магнитного поля постоянного магнита с магнитными полями проводников с током (движущихся заряженных частиц).
Магнитные силы — силы, действующие со стороны магнитного поля на находящиеся в нём магниты, проводники с током или движущиеся заряды.
Взаимодействие проводников с током
Открытие Эрстеда активизировало исследования по установлению связи между электрическими и магнитными явлениями. Ампер в 1820 г. провёл ряд экспериментов по изучению взаимодействия двух гибких первоначально расположенных прямолинейно и параллельно проводников с током. Он установил, что когда ток в проводниках проходит в противоположных направлениях, они отталкиваются (рис. 140, а), а когда в одинаковых направлениях — притягиваются (рис. 140, б). При отсутствии тока в проводниках они не проявляют магнитного взаимодействия (рис. 140, в). 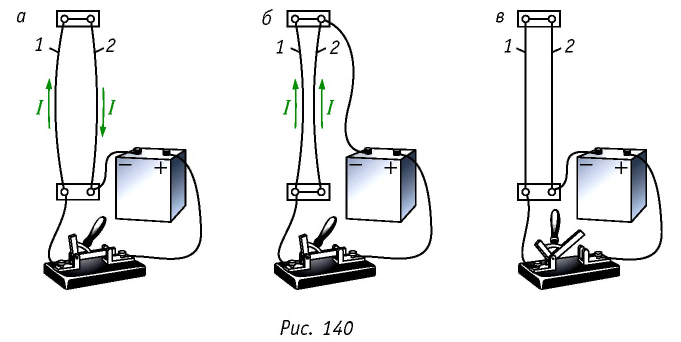
Магнитное поле одного проводника с током взаимодействует с током другого проводника посредством магнитной силы.
Магнитное взаимодействие двух параллельных проводников с током используют в СИ для определения единицы силы тока — ампера.
1 ампер — это сила неизменяющегося тока, который при прохождении по каждому из двух параллельных прямолинейных проводников бесконечной длины и ничтожно малого кругового сечения, расположенных на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, модуль которой равен 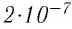
Действие магнитного поля на рамку с током
Действие магнитного поля на проводник с током проявляется не только в притяжении пли отталкивании. Проведём опыт. Подвесим около длинного тонкого вертикально расположенного проводника на тонких и гибких подводящих проводах маленькую (по сравнению с расстоянием, на котором магнитное поле заметно изменяется, т. е. подальше от проводника) рамку (рис. 141, а). При пропускании по проводнику и рамке электрического тока рамка поворачивается и располагается так, что оказывается в одной плоскости с проводником с током (рис. 141, б). Таким образом, магнитное поле оказывает на рамку с током ориентирующее действие, аналогичное действию на стрелку компаса.
Проведём ещё один опыт. Поместим проволочную рамку между полюсами постоянного подковообразного магнита. Если по рамке проходит ток, она устанавливается так, что её плоскость становится перпендикулярной прямой, соединяющей полюса магнита (рис. 142). В данном случае магнитное поле подковообразного магнита также оказывает на рамку с током ориентирующее действие.

Индукция магнитного поля
Для описания электростатического поля используют его основную характеристику — напряжённость 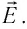
Направление индукции магнитного поля
Основной характеристикой, используемой для описания магнитного поля, является физическая векторная величина — индукция магнитного поля 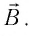
Для определения направления индукции магнитного поля 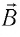
За направление индукции магнитного поля в данной точке поля принимают направление от южного полюса S к северному полюсу N свободно устанавливающейся магнитной стрелки, расположенной в рассматриваемой точке (рис. 143).
В магнитном поле прямолинейного проводника с током магнитные стрелки располагаются по касательным к окружностям (рис. 144), центры которых лежат на оси проводника.
На практике часто приходится иметь дело с магнитными полями электрических токов, проходящих по катушкам (соленоидам). В магнитном поле катушки с током магнитные стрелки устанавливаются по касательным к замкнутым кривым, охватывающим витки катушки (рис. 145).
Линии индукции магнитного поля
Распределение электростатического поля в пространстве можно сделать «видимым», используя представление о линиях напряжённости. Исследуя магнитное поле, создаваемое проводником с током или постоянным магнитом, с помощью магнитной стрелки в каждой точке пространства можно определить направление индукции магнитного поля. Такое исследование позволяет графически представить магнитное поле в виде линий магнитной индукции.
Линии индукции магнитного поля — воображаемые линии в пространстве, касательные к которым в каждой точке совпадают с направлением индукции магнитного поля (рис. 146).
Линии индукции магнитного поля непрерывны (не имеют ни начала, ни конца), замыкаются сами на себя. Это характерно для любых магнитных полей. Поля, обладающие таким свойством, называют вихревыми.
Очевидно, что через любую точку в магнитном поле можно провести только одну линию индукции. Поскольку индукция магнитного поля в любой точке пространства имеет определённое направление, то и направление линии индукции в каждой точке этого поля может быть только единственным. Это означает, что линии магнитной индукции, так же как и линии напряжённости электрического поля, не пересекаются.
Направление линий индукции магнитного поля
Определить направление линий индукции магнитного поля можно, используя правило буравчика: если поступательное движение буравчика совпадает с направлением тока, то рукоятка буравчика поворачивается в направлении линий индукции магнитного поля. В случае прямолинейного проводника с током линии индукции магнитного поля представляют собой концентрические окружности, которые находятся в плоскостях, перпендикулярных к проводнику (рис. 147).
Определить направление линии индукции магнитного поля прямолинейного проводника с током можно также с помощью правила правой руки: если мысленно обхватить проводник правой рукой так, чтобы большой палец указывал направление тока, то остальные пальцы окажутся согнуты в направлении линий индукции магнитного поля (рис. 148).
Картину линий индукции магнитного поля можно получить, используя мелкие железные опилки, которые в магнитном поле ведут себя как магнитные стрелки. На рисунке 149 представлена картина магнитного поля прямолинейного участка проводника с током. Картина магнитного поля кругового витка с током и графическое изображение линий индукции представлены на рисунках 150, а, б. 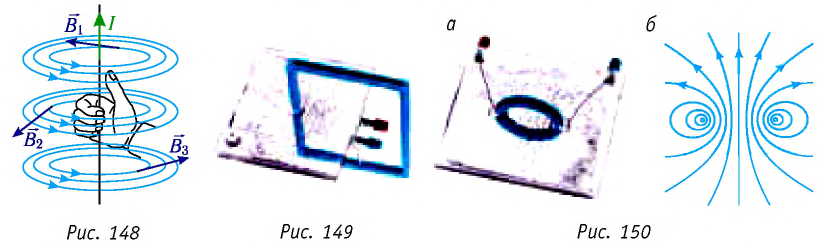
Полагают, что линии индукции магнитного поля, созданного постоянным магнитом, направлены внутри магнита от его южного полюса S к северному N (рис. 151).
Магнитное поле соленоида подобно полю полосового магнита. На рисунках 152, а, б представлена картина магнитного поля соленоида с током и дано графическое изображение линий индукции. Соленоид представляет собой цилиндрическую катушку, на которую виток к витку намотан провод, изолированный тонким слоем лака. Если длина соленоида много больше его диаметра, то внутри центральной части соленоида линии индукции магнитного поля практически параллельны и направлены вдоль его оси.
Однородное магнитное поле — поле, индукция которого во всех точках пространства одинакова.
Линии индукции такого поля параллельны. В противном случае поле называют неоднородным. Магнитное поле внутри длинного соленоида практически однородно, а вблизи краёв — неоднородно. Неоднородно и магнитное поле прямолинейного проводника с током (см. рис. 148).
Для наглядности на рисунках линии индукции изображают гуще в тех местах магнитного поля, где больше значение индукции магнитного поля (рис. 152, б). При этом на линии индукции указывают стрелкой направление индукции магнитного поля. Для крайних витков соленоида магнитное поле «кругового» витка с током, проходящим в направлении движения часовой стрелки, эквивалентно полю южного полюса постоянного магнита, а магнитное поле «кругового» витка с током, проходящим против направления движения часовой стрелки, эквивалентно полю северного полюса постоянного магнита (правило часовой стрелки) (рис. 153).
Определение направления индукции магнитного поля
Для определения направления индукции магнитного поля можно воспользоваться любым из правил, сформулированных выше. Причём, пользуясь правилом буравчика, надо помнить, что направление тока — это направление упорядоченного движения положительных зарядов. Если на рисунке изображён прямолинейный проводник с током, расположенный перпендикулярно плоскости страницы (рис. 155), и при этом ток направлен от читателя, то его условно обозначают крестиком (рис. 156, а); в случае, если ток направлен к читателю, — точкой (рис. 156, б). Так же (точкой или крестиком) обозначают направления векторов (индукции магнитного поля, силы и др.), расположенных перпендикулярно плоскости рисунка.
Полюсы соленоида, а следовательно, и направление индукции магнитного поля можно определить по правилу часовой стрелки (см. рис. 153) или правилу буравчика: если направление вращения рукоятки буравчика совпадает с направлением тока в витке, то поступательное движение острия буравчика укажет направление индукции магнитного поля внутри соленоида, а следовательно, и положение его северного полюса.
Пример №12
Электроны, образующие «электронный луч», движутся так, как изображено на рисунке 157, а. Определите направление линий индукции магнитного поля, создаваемого этими электронами.
Решение. Определить направление линий индукции магнитного поля, создаваемого движущимися электронами, можно как по правилу буравчика, так и по правилу правой руки. Однако следует помнить, что эти правила сформулированы для движущихся положительных зарядов. Поэтому в данном случае надо учесть, что за направление электрического тока принято направление, противоположное движению электронов. Тогда, если смотреть на линию индукции по направлению движения электронов, она будет сориентирована против направления движения часовой стрелки (рис. 157, б).
Пример №13
На рисунке 158 указано направление электрического тока в соленоиде. Определите магнитные полюсы соленоида.
Решение. Для определения магнитных полюсов соленоида можно воспользоваться как правилом буравчика, так и правилом часовой стрелки. В первом случае будем мысленно вращать буравчик по направлению тока в витках соленоида. Остриё буравчика при этом перемещается вдоль оси соленоида от торца А к торцу В. Так как линии индукции внутри магнита направлены от южного полюса к его северному полюсу, то по аналогии можно сделать вывод, что у торца А — южный полюс соленоида, а у торца В — северный.
Проверим свой вывод, применив правило часовой стрелки. Если смотреть со стороны торца А соленоида, то видно, что направление тока в витке совпадает с направлением движения часовой стрелки. Следовательно, у торца А — южный полюс, а у торца В — северный.
Видео:Урок 218. Напряженность электрического поляСкачать

Сила Ампера
Для количественного описания магнитного поля необходимо знать не только направление индукции магнитного поля, но и её модуль. Характеристики электростатического поля определяют с помощью пробного заряда. Для определения характеристик магнитного поля используют «пробный» ток, который представляет собой малый участок проводника (элемент тока).
Модуль индукции магнитного поля
Действие магнитного поля на находящийся в нём малый участок проводника с током экспериментально исследовал Ампер, осуществив опыты с различными проводниками, входящими в замкнутые электрические цепи. В 1820 г. Ампер установил, что модуль силы, которой однородное магнитное поле действует на прямолинейный участок проводника с током, зависит от величин, характеризующих этот проводник. Этими величинами являются сила тока 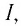
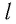
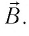
Из опытов следует, что модуль силы, действующей со стороны однородного магнитного поля на прямолинейный участок проводника с током, пропорционален силе тока 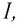
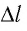
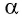
Эта сила названа в честь А.-М. Ампера силой Ампера.
Так как 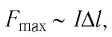
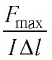
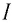
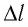
Индукция магнитного поля — физическая векторная величина, модуль которой равен отношению максимального значения силы, действующей со стороны магнитного поля на прямолинейный участок проводника с током, к произведению силы тока в нём и длины этого участка:
Таким образом, в каждой точке магнитного поля могут быть определены как направление индукции магнитного поля, так и её модуль.
В СИ индукцию магнитного поля измеряют в теслах (Тл) в честь сербского инженера и изобретателя Николы Теслы (1856—1943), с 1884 г. работавшего в США.
1 Тл — индукция однородного магнитного поля, в котором на прямолинейный участок проводника длиной 1 м при силе тока в нём 1 А действует со стороны поля максимальная сила, модуль которой 1 Н.
Видео:ЭЛЕКТРОДИНАМИКА. ПОСТОЯННЫЙ ТОК I Финальный Курс I ЕГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

Закон Ампера
Из выражения (29.1) следует, что максимальное значение силы Ампера:
Экспериментально доказано, что в общем случае модуль силы Ампера можно рассчитать по формуле
Выражение (29.2) называют законом Ампера.
Направление силы Ампера определяют по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная к проводнику составляющая индукции магнитного поля входила в ладонь, четыре вытянутых пальца были направлены по току, то отогнутый на 90° в плоскости ладони большой палец укажет направление силы Ампера, действующей на прямолинейный участок проводника с током (рис. 164).
Принцип суперпозиции магнитных полей
В случае, когда магнитное поле создаётся несколькими источниками, индукцию результирующего магнитного поля можно определить по принципу суперпозиции: если магнитное поле в некоторой точке пространства создаётся не одним, а несколькими электрическими токами (или движущимися зарядами), то индукция результирующего магнитного поля в этой точке равна векторной сумме индукций магнитных полей, созданных каждым током (движущимся зарядом):
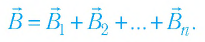
Пример №14
В однородном магнитном поле, индукция которого направлена вертикально и её модуль В = 0,50 Тл, на лёгких проводах горизонтально подвешен прямолинейный металлический стержень длиной 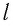
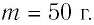
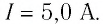
Решение. На стержень действуют силы упругости проводов 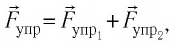
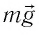
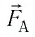
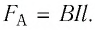
сил равна нулю: 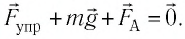
следовательно,
Ответ:
Видео:2.5 Граничные условия для векторов поля на поверхности раздела средСкачать
Сила Лоренца
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?
Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в месть выдающегося нидерландского физика Хендрика Антона Лоренца (1853—1928).
Модуль силы Лоренца можно определить по формуле 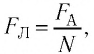
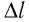
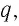
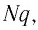
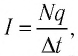
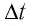
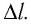
Поскольку 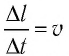
где 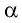
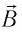
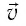
Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля 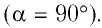
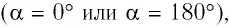
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.
* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем.
Сила Лоренца перпендикулярна как направлению скорости 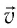
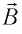
Движение заряженных частиц в однородном магнитном поле
Под действием силы Лоренца частицы, имеющие электрический заряд, движутся в магнитном поле по криволинейным траекториям. Причём если в данной инерциальной системе отсчёта направление скорости движения частицы перпендикулярно направлению индукции однородного магнитного поля 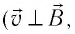
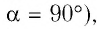
Пусть в однородном магнитном поле, индукция которого 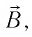
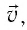
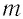
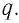
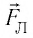
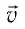
В результате частица движется по окружности, радиус которой можно определить из формулы
Период Т обращения частицы, движущейся по окружности в однородном магнитном поле:
Как следует из выражения (30.2), период обращения частицы не зависит от модуля скорости её движения и радиуса траектории, а определяется только модулем заряда частицы, её массой и значением индукции магнитного поля.
Интересно знать:
Поскольку сила Лоренца направлена под углом 90° к скорости движения заряженной частицы в каждой точке траектории (рис. 171), то работа этой силы при движении заряженной частицы в магнитном поле равна нулю. Поэтому кинетическая энергия частицы, движущейся в стационарном (не изменяющемся во времени) магнитном поле, не изменяется, т. е. стационарное магнитное поле нельзя использовать для ускорения заряженных частиц.
Увеличение кинетической энергии частицы, т. е. её разгон, возможно под действием электрического поля (в этом случае изменение кинетической энергии частицы равно работе силы поля). Поэтому в современных ускорителях (рис. 172) заряженных частиц электрическое поле используют для ускорения, а магнитное — для «формирования» траектории движения заряженных частиц.
Пример №15
Электрон движется в однородном магнитном поле по окружности радиусом 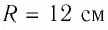
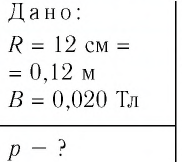
Решение. Но определению модуль импульса электрона 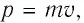
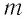
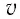
На электрон в магнитном поле действуют сила Лоренца и сила тяжести, модуль которой во много раз меньше модуля силы Лоренца. Поэтому действием силы тяжести на движущуюся в магнитном поле заряженную частицу можно пренебречь. Согласно второму закону Ньютона 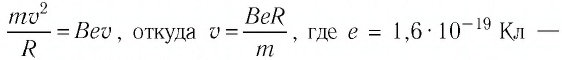
Следовательно,
Ответ:
Видео:Вся ЭЛЕКТРОДИНАМИКА за 4 часа для ЕГЭ 2023 по физикеСкачать

Магнитный поток
После опытов Эрстеда и Ампера стало понятно, что электрические и магнитные поля имеют одни и те же источники: движущиеся электрические заряды. Это позволило предположить, что они каким-то образом связаны друг с другом. Фарадей был абсолютно уверен в единстве электрических и магнитных явлений. Вскоре после открытия Эрстеда в своём дневнике в декабре 1821 г. Фарадей записал: «Превратить магнетизм в электричество». На решение этой фундаментальной задачи ему понадобилось десять лет. После многочисленных экспериментов Фарадей сделал эпохальное открытие — замыкая и размыкая электрическую цепь одной катушки, он в замкнутой цепи другой катушки получил электрический ток. Наблюдаемое явление Фарадей назвал электромагнитной индукцией.
Индукция магнитного поля характеризует магнитное поле в конкретной точке пространства. Чтобы охарактеризовать магнитное поле во всех точках поверхности, ограниченной замкнутым контуром, ввели физическую величину, которую назвали магнитным потоком (потоком индукции магнитного поля).
Магнитный поток через плоскую поверхность, находящуюся в однородном магнитном поле, — физическая скалярная величина, равная произведению модуля индукции магнитного поля, площади поверхности и косинуса угла между направлениями нормали к этой поверхности и индукции магнитного поля (рис. 173):
Единицей магнитного потока в СИ является вебер (Вб). 1 Вб — магнитный поток однородного магнитного поля индукцией I Тл через плоскую поверхность, расположенную перпендикулярно индукции магнитного поля, площадь которой
Формула (31.1) позволяет сделать вывод, что магнитный поток зависит от взаимной ориентации линий индукции магнитного поля и нормали к плоской поверхности. Магнитный поток максимален, если 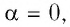
Если плоская поверхность параллельна линиям индукции 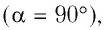
На практике часто встречаются ситуации, когда линии индукции магнитного поля пересекают поверхности, ограниченные не одним контуром, а несколькими. Так, например, линии индукции могут пересекать поверхности, ограниченные витками соленоида, которые «параллельны» друг другу и имеют одинаковую площадь поверхности. В этом случае магнитный поток определяют по формуле
где N — число витков соленоида; S — площадь поверхности, ограниченной каждым витком.
Изменить магнитный поток через поверхность, ограниченную контуром, можно, изменяя: 1) индукцию магнитного поля, в котором находится контур; 2) размеры этого контура; 3) ориентацию контура в магнитном поле.
Явление электромагнитной индукции
В 1831 г. Фарадей провёл серию опытов, которые позволили установить следующие факты:
1) при движении постоянного магнита относительно катушки, подключённой к гальванометру, в катушке возникал электрический ток (стрелка гальванометра отклонялась). Причём направление тока изменялось на противоположное при изменении направления движения магнита. Это же явление происходило, если магнит был неподвижен, а двигали катушку (рис. 174);
2) в катушке, подключённой к гальванометру, возникал электрический ток, если относительно неё двигали другую катушку, которая была подключена к источнику постоянного тока (рис. 175);
3) если две катушки намотаны на общий каркас и одну подключали к гальванометру, а другую — к источнику тока, то ток в первой катушке возникал при изменении тока во второй (рис. 176).
Во всех рассмотренных случаях электрический ток в цепи гальванометра возникал только при изменении магнитного потока через поверхности, ограниченные витками катушки, подключённой к гальванометру (рис. 177). Причём значение силы тока, возникающего в контуре, не зависело от способа изменения магнитного потока, а определялось только скоростью его изменения. Назвали такой ток индукционным током.
Индукционным ток — электрический ток, возникающий в замкнутом проводящем контуре при любом изменении магнитного потока через поверхность, ограниченную этим контуром.
Для существования тока в замкнутой электрической цепи необходимо, чтобы на свободные заряженные частицы действовали сторонние силы, т. е. в цепи должен быть источник ЭДС. Очевидно, что в опытах Фарадея источником этих сторонних сил являлся изменяющийся магнитный поток, который создавал в цепи ЭДС. Эту ЭДС назвали электродвижущей силой индукции или ЭДС индукции. Если цепь замкнута, ЭДС индукции создаёт индукционный ток, т. е. возникновение индукционного тока является вторичным эффектом.
Электромагнитная индукция — явление возникновения ЭДС индукции в контуре, который либо покоится в изменяющемся во времени магнитном поле, либо движется в постоянном магнитном поле так, что магнитный поток через поверхность, ограниченную контуром, меняется.
Из истории физики
Один из историков науки писал: «. работы других учёных — Кулона, Гальвани, Эрстеда, Араго, Ампера — представляли собой отдельные пики, тогда как Фарадей воздвиг «горную цепь» из взаимосвязанных работ».
Правило Ленца
Открыв явление электромагнитной индукции, Фарадей практически за полтора месяца установил все его существенные закономерности. Ему стала понятна сущность явления, которое сыграло такую важную роль для человечества: во всех экспериментах, проведённых им, индукционный ток в проводящем контуре возникал в результате изменения магнитного потока через поверхность, ограниченную этим контуром. Фарадей не только открыл явление электромагнитной индукции, но и первым продемонстрировал, «что можно создать постоянный ток электричества при помощи обыкновенных магнитов», сконструировав устройство, позволяющее преобразовывать механическую энергию в электрическую.
Направление индукционного тока.
Опыты Фарадея показали, что направление индукционного тока, вызванного возрастанием магнитного потока, противоположно направлению индукционного тока, вызванного его уменьшением. Исследовав явление электромагнитной индукции, петербургский академик Эмилий Христианович Ленц (1804—1865) в 1833 г. сформулировал правило для определения направления индукционного тока (правило Ленца): возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором создаваемый им магнитный поток через поверхность, ограниченную контуром, противодействует изменению магнитного потока, вызывающему этот индукционный ток. Это означает, что при возрастании магнитного потока магнитное поле индукционного тока направлено против внешнего поля, а при убывании — магнитное поле индукционного тока направлено так же, как и внешнее поле.
В более сжатой форме правило Ленца можно сформулировать следующим образом: индукционный ток всегда направлен так, что его действие противоположно действию причины, вызвавшей этот ток.
Правило Ленца можно проиллюстрировать, используя два алюминиевых кольца (одно из них с разрезом), закреплённых на стержне, свободно вращающемся вокруг вертикальной оси (рис. 178).
Из опыта следует, что при приближении постоянного магнита к сплошному кольцу оно отталкивается от магнита; при удалении магнита — кольцо притягивается к нему. Отталкивание и притяжение сплошного кольца объясняют возникновением в нём индукционного тока при изменении магнитного потока через поверхность, ограниченную кольцом. Очевидно, что при приближении магнита к кольцу направление индукционного тока таково, что индукция магнитного поля тока противоположна индукции магнитного поля постоянного магнита (рис. 179). При удалении магнита индукции магнитных полей тока и магнита совпадают по направлению. При движении магнита относительно кольца с разрезом взаимодействие не наблюдается, так как индукционный ток отсутствует.
Чтобы определить направление индукционного тока по правилу Ленца, необходимо выполнить следующие операции (рис. 180):
- определить направление линий индукции внешнего магнитного поля
- выяснить, увеличивается или уменьшается магнитный поток через поверхность, ограниченную проводящим контуром;
- определить направление линий индукции магнитного поля индукционного тока
: если приращение магнитного потока
то направления индукций внешнего магнитного поля
и магнитного поля индукционного тока
совпадают, если
то — противоположны;
- зная направление линий индукции магнитного поля индукционного тока
по правилу буравчика (правилу часовой стрелки) определить направление индукционного тока.
Правило Ленца соответствует закону сохранения энергии применительно к явлению электромагнитной индукции. В самом деле, если бы индукционный ток имел другое направление, он мог бы существовать без затрат энергии, что противоречит закону сохранения энергии.
Открытие явления электромагнитной индукции имело большое значение. Была доказана взаимосвязь магнитных и электрических явлений, что послужило в дальнейшем отправным пунктом для разработки теории электромагнитного поля.
Закон электромагнитной индукции
Анализируя результаты опытов Фарадея, Максвелл в 1873 г. пришёл к выводу, что ЭДС индукции в замкнутом проводящем контуре пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром, т. е.
Чтобы обеспечить строгое равенство в выражении (32.1), необходимо учесть направление индукционного тока. Согласно правилу Ленца при увеличении магнитного потока 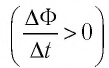
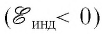
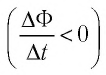
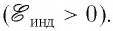
Таким образом, ЭДС электромагнитной индукции в контуре равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой с противоположным знаком.
Выражение (32.2) называют законом электромагнитной индукции Фарадея, подчёркивая этим заслуги учёного в изучении указанного явления. Следует отметить, что данный закон является универсальным, т. е. ЭДС индукции не зависит от способа изменения магнитного потока.
Зная ЭДС индукции, можно определить силу индукционного тока. Согласно закону Ома для полной цепи:
где R — сопротивление проводника, из которого изготовлен замкнутый проводящий контур.
Пример №16
Определите направление индукционного тока в соленоиде, изображённом на рисунке 183.
Решение. При приближении северного полюса магнита к соленоиду в нём индуцируется электрический ток такого направления, при котором ближайший к магниту конец соленоида приобретает свойства северного магнитного полюса. Определяя направление тока по правилу буравчика (правилу часовой стрелки), отмечаем, что ток в соленоиде направлен от точки А к точке В. При удалении северного полюса магнита от соленоида в нём возникает индукционный ток, направленный от точки В к точке А.
Явление самоиндукции
Фарадей опытным путём установил, что электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри (1797— 1878) независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 г. Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Каков механизм возникновения ЭДС индукции в этом случае?
Самоиндукция:
Если электрический ток, проходящий в замкнутом проводящем контуре, по каким-либо причинам изменяется, то изменяется и магнитное поле, создаваемое этим током. Это влечёт за собой изменение магнитного потока через поверхность, ограниченную контуром. Поскольку магнитный поток Ф пропорционален модулю магнитной индукции В поля, который, в свою очередь, пропорционален силе тока 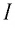
Коэффициенту пропорциональности между магнитным потоком Ф и силой тока 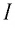
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб. Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Если электрический ток, проходящий в контуре, изменяется, то он создаёт изменяющийся магнитный поток, что приводит к появлению ЭДС индукции. Это явление назвали самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи.
Возникающую в этом случае ЭДС назвали электродвижущей силой самоиндукции. Согласно закону электромагнитной индукции,
Если индуктивность контура не изменяется во времени, т. е. 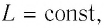
Поскольку контур замкнут, ЭДС самоиндукции создаёт в нём ток самоиндукции. Силу тока самоиндукции можно определить по закону Ома 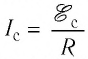
R — сопротивление контура. Согласно правилу Ленца, ток самоиндукции всегда направлен так, чтобы противодействовать изменению тока, создаваемого источником. При возрастании силы тока ток самоиндукции направлен против тока источника, а при уменьшении — направления тока источника и тока самоиндукции совпадают.
Наблюдение самоиндукции:
Для наблюдения явления самоиндукции соберем электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока. Схема цепи представлена на рисунке 185. При замыкании ключа лампочка 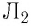
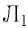
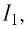
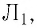
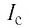
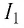

Энергия магнитного поля
Явление самоиндукции можно наблюдать и при размыкании электрической цепи. Если включить лампочку параллельно катушке в электрическую цепь постоянного тока, то при размыкании цепи можно увидеть, что лампочка ярко вспыхивает. Почему это происходит? При размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки.
Откуда берётся энергия, обеспечивающая вспышку лампочки? Это не энергия источника тока, так как он уже отсоединён. Вспышка лампочки происходит одновременно с уменьшением силы тока в катушке и создаваемого током магнитного поля. Можно предположить, что запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
Расчёты подтверждают, что энергию магнитного поля можно определить по формуле
где L — индуктивность контура; 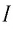
Пример №17
На рисунке 186 представлен график зависимости силы тока, проходящего по соленоиду, от времени. Определите максимальное значение модуля ЭДС самоиндукции в соленоиде, если его индуктивность
Решение. ЭДС самоиндукции 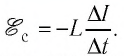
1) от момента времени 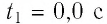
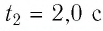
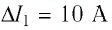
2) от момента времени 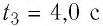
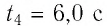
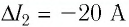
3) от момента времени 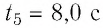
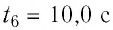
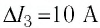
Поскольку промежутки времени 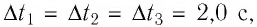
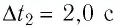
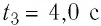
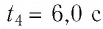
Таким образом, 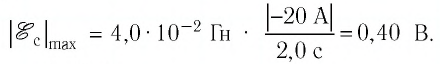
Ответ:
Пример №18
На рисунке 187 представлен график зависимости ЭДС самоиндукции, возникающей в катушке с индуктивностью 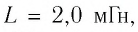
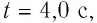
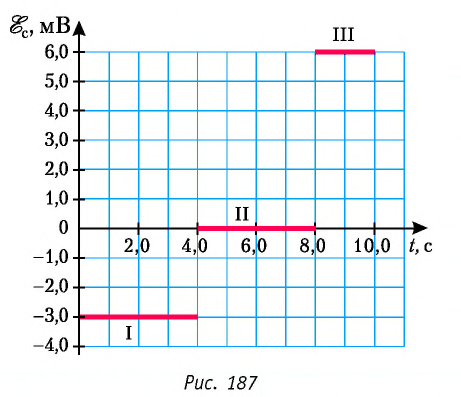
Решение. Анализируя график, можно сделать вывод, что на участке I ЭДС самоиндукции 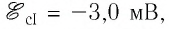
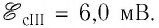
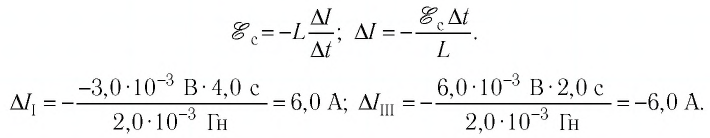
На участке II графика 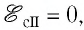
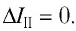
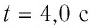
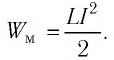
Ответ:
Видео:Урок 222. Поток вектора напряженности электрического поляСкачать

Электрический ток в различных средах
При изучении электрических явлении необходимо знать, возможно ли существование электрического тока в рассматриваемом веществе, поскольку все вещества делят на группы по их электрическим свойствам: проводники, полупроводники, диэлектрики. Чем эти группы веществ отличаются друг от друга? Как они проводят электрический ток?
Проводниками электрического тока могут быть вещества и в твёрдом, и в жидком, и в газообразном состояниях. Изучая данную тему, найдём ответы на следующие вопросы: какие частицы являются носителями электрического заряда в данной среде? Как зависит электрическая проводимость среды от температуры, излучения и других воздействий? Каково техническое применение электрического тока в различных средах?
Электрический ток в металлах
(Типичными представителями класса проводников являются металлы. Какова природа электрического тока в металлах?
Природа электрического тока в металлах
В металлических проводниках носители электрического заряда — свободные электроны. 11од действием внешнего электрического поля свободные электроны упорядочение движутся, создавая электрический ток (рис. 194). Электронная проводимость металлов была впервые экспериментально подтверждена немецким физиком К. Рикке (1845-1915) в 1901 г.
Суть опыта Рикке заключалась в следующем: по проводнику, состоявшему из трёх отполированных и плотно прижатых друг к другу цилиндров — двух медных и одного алюминиевого (рис. 195), в течение года проходил ток одного и того же направления. За этот промежуток времени через проводник прошёл заряд более 3,5 МКл. После завершения опыта взвешивание показало, что массы цилиндров остались неизменными. Это явилось экспериментальным доказательством того, что перенос заряда при прохождении тока в металлах не сопровождается химическими процессами и переносом вещества, а осуществляется частицами, которые являются одинаковыми для всех металлов, т. е. электронами.
Вещества, обладающие электронной проводимостью, называют проводниками первого рода.
В соответствии с классической электронной теорией проводимости металлов, созданной немецким физиком П. Друде (1863-1906) в 1900 г., металлический проводник можно рассматривать как физическую систему, состоящую из свободных электронов и положительно заряженных ионов, колеблющихся около положений равновесия (рис. 196).
Из истории физики:
Убедительное доказательство электронной природы тока в металлах было получено в опытах с проявлением инерции электронов. Идея таких опытов и первые результаты (1913 г.) принадлежали русским физикам Л. И. Мандельштаму (1879-1944) и Н. Д. Папалекси (1880-1947).
В 1916 г. американские учёные Р. Толмен (1881-1948) и Т. Стюарт (1890-1958) усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением свободных электронов.
Зависимость сопротивления металлов от температуры
При изучении физики в 8-м классе вы узнали, что сопротивление металлических проводников зависит от рода вещества (удельного сопротивления р) и их геометрических размеров (длины 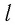
А зависит ли сопротивление от температуры проводника?
Проведём опыт. Соберём электрическую цепь, состоящую из источника тока, проволочной спирали и гальванометра (рис. 197). Из опыта следует, что при нагревании спирали показания гальванометра уменьшаются. Вывод очевиден: при увеличении температуры сопротивление металлов увеличивается.
Зависимость сопротивления металлов от температуры используют в специальных приборах — термометрах сопротивления (рис. 198).
Широкое распространение получили термометры сопротивления из чистых металлов, особенно платины и меди, которые конструктивно представляют собой металлическую проволоку, намотанную на жёсткий каркас (из кварца, фарфора, слюды), заключённый в защитную оболочку (из металла, кварца, фарфора, стекла) (рис. 199). Платиновые термометры сопротивления применяют для измерения температуры в пределах от —263 до 1064°С, медные — от -50 до 180°С.
Сверхпроводимость
При очень низких температурах сопротивление некоторых металлических проводников резко (скачком) уменьшается до нуля. Впервые это обнаружил в 1911 г. нидерландский физик Г. Камерлинг-Оннес (1853— 1926). Он экспериментально установил, что при температуре 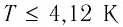
Если в сверхпроводнике создать электрический ток, то он будет существовать в нём неограниченно долго. При этом для поддержания тока нет необходимости в источнике тока. Это указывает на перспективу использования явления сверхпроводимости при передаче электрической энергии.
Сверхпроводящие соединения нашли применение в качестве материала обмоток электромагнитов для создания сильных магнитных полей в мощных электрических двигателях, генераторах, ускорителях и др. Разрабатывают проекты сверхпроводящих электронно-вычислительных машин. Уже созданы компактные интегральные схемы на сверхпроводниках, обладающие рядом преимуществ по сравнению с имеющимися аналогами.
Электрический ток в электролитах
При изучении предыдущего параграфа вы узнали, что в металлах перенос заряда не сопровождается переносом вещества, а носителями свободных зарядов являются электроны. Но существует класс проводников, прохождение электрического тока в которых всегда сопровождается химическими изменениями и переносом вещества. Какова природа электрического тока в таких проводниках?
Природа электрического тока в электролитах
Из опытов следует, что растворы многих солей, кислот и щелочей, а также расплавы солей и оксидов металлов проводят электрический ток, т. е. являются проводниками. Такие проводники назвали электролитами.
Электролиты — вещества, растворы или расплавы которых проводят электрический ток.
Проведём опыт. Соберём электрическую цепь, состоящую из источника тока, лампы накаливания и ванны с дистиллированной водой, в которой находятся два угольных электрода. При замыкании цепи лампа не светится, следовательно, дистиллированная вода не проводит электрический ток. Повторим опыт, добавив в дистиллированную воду сахар.
Лампа не светится и в этом случае. Раствор сахара в воде также не является проводником. А теперь добавим в дистиллированную воду небольшое количество соли, например, хлорида меди(II) 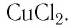
Изучая химию, вы узнали, что при растворении солей, кислот и щелочей в воде происходит электролитическая диссоциация, т. е. распад молекул электролита на ионы. В проведённом опыте хлорид меди(II) 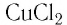
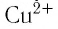
Ионы 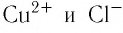
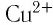
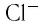
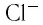
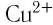
Электролиз — процесс выделения на электроде вещества, связанный с окислительно-восстановительными реакциями, протекающими при прохождении электрического тока через растворы (расплавы) электролитов.
Таким образом, свободные носители электрического заряда в электролитах — положительно и отрицательно заряженные ионы, которые образуются в результате электролитической диссоциации, а проводимость электролитов является ионной. Электролиты относят к проводникам второго рода.
Техническое применение электролиза
Электролиз нашёл различные применения в промышленности. Рассмотрим некоторые из них.
1. Нанесение защитных и декоративных покрытий на металлические изделия (гальваностегия).
Для предохранения металлов от окисления, а также для придания изделиям прочности и улучшения внешнего вида их покрывают тонким слоем благородных металлов (золотом, серебром) или малоокисляющимися металлами (хромом, никелем).
Предмет, подлежащий гальваническому покрытию, например, ложку (рис. 202), погружают в качестве катода в электролитическую ванну. Электролитом является раствор соли металла, которым осуществляется покрытие. Анодом служит пластина из такого же металла. Пропуская через электролитическую ванну в течение определённого промежутка времени электрический ток. ложку покрывают слоем металла нужной толщины. Для наиболее равномерного покрытия ложки её необходимо поместить между двумя или более анодными пластинами. После покрытия ложку вынимают из ванны, сушат и полируют.
2. Производство металлических копий с рельефных моделей(гальванопластика).
Для получения копий предметов (монет, медалей, барельефов и т. п.) делают слепки из какого-нибудь пластичного материала (например, воска). Для придания слепку электропроводности его покрывают графитовой пылью, погружают в электролитическую ванну в качестве катода и получают на нём слой металла нужной толщины. Затем, нагревая, удаляют воск.
Процесс гальванопластики был разработан в 1836 г. русским академиком Б. С. Якоби (1801-1874).
3. Получение металлов из расплавленных руд и их очистка, электрохимическая обработка металлов.
Процесс очистки металлов происходит в электролитической ванне. Анодом служит металл, подлежащий очистке, катодом — тонкая пластина из чистого металла, а электролитом — раствор соли данного металла. Например, пластину из неочищенной меди помещают в качестве анода в ванну с раствором медного купороса, где катодом служит лист чистой меди (рис. 203). В загрязнённых металлах могут содержаться ценные примеси. Так, в меди часто содержатся никель и серебро. При пропускании через ванну электрического тока медь с анода переходит в раствор, из раствора на катоде выделяется чистая медь, а примеси выпадают в виде осадка или переходят в раствор.
Электрический ток в газах
Газы при нормальных условиях не проводят электрический ток, т. е. являются диэлектриками. Это обусловлено тем, что газы состоят из нейтральных атомов (молекул). Однако при определённых условиях газы, в том числе и воздух, становятся проводниками. При каких условиях это возможно?
Природа электрического тока в газах
Проведём опыт и убедимся, что электрическая проводимость газа (воздуха) может изменяться. Два металлических диска, заряженных разноимёнными зарядами и расположенных на некотором расстоянии друг от друга, соединим с электрометром (рис. 204). Стрелка электрометра при этом отклонится на некоторый угол.
Электрометр не разряжается, значит, при небольшой разности потенциалов между дисками воздух не проводит электрический ток.
Повторим опыт, нагревая пламенем (спиртовки, свечи) воздушный промежуток между дисками. Электрометр разряжается, т. е. через воздух проходит электрический ток (рис. 205).
Вывод очевиден: в воздушном промежутке между дисками появились свободные носители электрического заряда.
Если убрать пламя, то электрический ток исчезнет, т. е. воздух между дисками опять станет диэлектриком.
Объясним результаты рассмотренного опыта. Нагревание газа пламенем приводит к образованию свободных электронов и положительно заряженных ионов, т. е. к ионизации газа.
Для отрыва электрона от атома (молекулы) необходима энергия, минимальное значение которой называют энергией ионизации атома (молекулы). Наряду с ионизацией может происходить присоединение образовавшихся при отрыве электронов к нейтральным атомам (молекулам) газа. Это приводит к образованию отрицательно заряженных ионов.
Под действием электрического поля в газе возникает направленное движение положительно заряженных ионов к отрицательному электроду (катоду) и направленное движение электронов и отрицательно заряженных ионов к положительному электроду (аноду). В ионизированном газе возникает электрический ток, который называют газовым разрядом.
Таким образом, носители электрического заряда в ионизированных газах — положительно и отрицательно заряженные ионы и свободные электроны, а проводимость газов является ионно-электронной.
Если устранить внешнее воздействие (в данном случае нагревание пламенем), электрический ток в газе прекращается. Это обусловлено тем, что при столкновении положительно заряженного иона с электроном они образуют нейтральный атом (молекулу) газа. Ионы противоположных знаков при столкновении также превращаются в нейтральные атомы (молекулы) — рекомбинируют. При рекомбинации освобождается энергия, равная энергии, затраченной на ионизацию.
Таким образом, чтобы в газе появились свободные носители электрического заряда, его атомы (молекулы) необходимо ионизировать. Это можно осуществить нагреванием газа до высокой температуры, воздействием на газ ультрафиолетовым, рентгеновским, радиоактивным излучениями и др.
Внешние воздействия, в результате которых происходит ионизация, называют ионизаторами. Разряд, возникающий в результате ионизации газа под действием ионизатора, называют несамостоятельным.
Однако в ряде случаев газовый разряд может существовать и после прекращения действия ионизатора. В этом случае имеющееся между электродами сильное электрическое поле является причиной сохранения газового разряда, который называют самостоятельным.
Виды самостоятельного газового разряда и их применение
В зависимости от напряжённости электрического поля, давления газа, формы и вещества электродов различают следующие виды самостоятельного газового разряда: тлеющий, дуговой, коронный и искровой.
Тлеющий разряд характеризуется небольшой силой тока (десятки миллиампер), относительно высоким напряжением (десятки и сотни вольт), низким давлением газа (десятые доли миллиметра ртутного столба). Тлеющий разряд широко используют в различных газосветных трубках (рис. 206), применяемых для световой рекламы и декораций, лампах дневного света (рис. 207), неоновых лампах.
Дуговой разряд представляет собой столб ярко светящегося газа (рис. 208). Он характеризуется большой силой тока (десятки и сотни ампер) и сравнительно небольшим напряжением (несколько десятков вольт). Дуговой разряд является мощным источником света. Его используют в осветительных установках, для сварки и резки металлов (рис. 209), электролиза расплавов, в промышленных электропечах для плавки стали и др.
Интересно знать:
В 1802 г. профессор физики Петербургской медико-химической академии В. В. Петров получил электрическую дугу. Он установил, что если присоединить к полюсам большой электрической батареи два кусочка древесного угля, привести их в соприкосновение, а затем слегка раздвинуть на небольшое расстояние, то между концами углей образуется яркое пламя, а сами концы углей раскаляются добела, испуская ослепительный свет (электрическая дуга). Впервые электрическая дуга была применена в 1876 г. русским инженером П. Н. Яблочковым для уличного освещения.
Коронный разряд возникает вблизи заострённой части проводника при атмосферном давлении под действием сильно неоднородного электрического поля. Он сопровождается слабым свечением, напоминающим корону, и характерным потрескиванием (рис. 210).
Коронный разряд используют в электрофильтрах для очистки промышленных газов от твёрдых и жидких примесей. Однако возникновение коронного разряда вокруг высоковольтных линий электропередачи нежелательно, так как приводит к потерям электрической энергии.
Интересно знать:
Часто перед грозой, во время шторма или снежной бури в атмосфере резко возрастает напряжённость электрического поля. Это приводит к возникновению слабого свечения вблизи заострённых предметов, например, вблизи корабельных мачт, шпилей на зданиях и др. (рис. 211). Моряки, бороздившие моря и океаны, часто наблюдали это явление (коронный разряд), которое получило название «огни Святого Эльма». Один из участников кругосветного плавания Магеллана писал: «Во время тех штормов нам много раз являлся сам Святой Эльм в виде света. чрезвычайно тёмными ночами на грот-мачте, где оставался в течение двух и более часов, избавляя нас от уныния».
Искровой разряд наблюдают при высоком напряжении (рис. 212). Он сопровождается ярким свечением газа, звуковым эффектом, который создаётся резким повышением давления воздуха. Примером искрового разряда в природе служит молния (рис. 213).
Интересно знать:
Перед появлением молнии напряжение между облаком и поверхностью Земли достигает 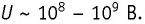
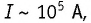
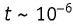
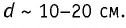
Плазма
При достаточно высокой температуре любое вещество испаряется, превращаясь в газ. При дальнейшем увеличении температуры усиливается термическая ионизация. Нейтральные молекулы газа распадаются на составляющие их атомы, которые в дальнейшем превращаются в ионы. Кроме того, ионизация газа может быть обусловлена его взаимодействием с электромагнитным излучением (фотоионизация) или бомбардировкой газа заряженными частицами, например, ионизация электронным ударом.
Плазма — полностью или частично ионизованный газ, в котором концентрации положительных и отрицательных зарядов практически совпадают, т. е. средние плотности положительных 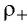
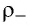
В зависимости от степени ионизации различают частично ионизованную и полностью ионизованную плазму. В зависимости от скорости теплового движения заряженных частиц различают низкотемпературную 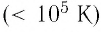
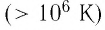
Плазма заполняет космическое пространство между Рис 214 звёздами и галактиками и является самым распространённым состоянием вещества во Вселенной (рис. 214). Концентрация плазмы в межгалактическом пространстве очень мала, в среднем одна частица на кубический метр. Верхний слой атмосферы Земли также представляет собой слабо ионизованную плазму. Причиной ионизации являются ультрафиолетовое и рентгеновское излучение Солнца и других звёзд, быстрые заряженные частицы и др.
Независимо от способа получения плазма в целом является электрически нейтральной. Проводимость плазмы растёт с увеличением отношения числа ионизованных атомов (молекул) к их общему числу. Полностью ионизованная плазма по своей проводимости приближается к сверхпроводникам.
Электрический ток в полупроводниках
Полупроводники — широкий класс как неорганических, так и органических веществ в твёрдом или жидком состоянии. Полупроводники обладают многими замечательными свойствами, благодаря которым они нашли широкое применение в различных областях науки и техники. Каковы особенности строения полупроводников?
Зависимость сопротивления полупроводников от температуры и освещённости
Удельное сопротивление полупроводников находится в пределах от 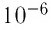
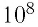
Изучить свойства полупроводников можно на опытах. Соберём электрическую цепь, состоящую из источника тока, полупроводника и миллиамперметра (рис. 215). Из опыта следует, что при нагревании полупроводника сила тока в цепи возрастает. Возрастание силы тока обусловлено тем, что при увеличении температуры сопротивление полупроводника уменьшается.
Проведём ещё один опыт. Изменяя освещённость поверхности полупроводника, наблюдаем изменение показаний миллиамперметра (рис. 216). Результаты наблюдений означают, что при освещении поверхности полупроводника его сопротивление уменьшается.
Таким образом, уменьшить сопротивление полупроводника можно, либо нагревая его, либо воздействуя электромагнитным излучением, например освещая его поверхность.
Природа электрического тока в полупроводниках
Экспериментально установлено, что при прохождении электрического тока в полупроводниках, как и в металлах, никаких химических изменений не происходит, т. е. перенос заряда при прохождении тока не сопровождается переносом вещества. Это свидетельствует о том, что свободными носителями электрического заряда в полупроводниках, как и в металлах, являются электроны.
Рассмотрим механизм проводимости полупроводников на примере кристалла германия Ge, валентность атомов которого равна четырём.
Атомы германия на внешней оболочке имеют четыре сравнительно слабо связанных с ядром валентных электрона. При этом каждый атом кристалла связан с четырьмя соседними атомами ковалентными связями. Два соседних атома объединяют два своих валентных электрона (по одному от каждого атома), которые образуют электронную пару. Поэтому все валентные электроны атома германия участвуют в образовании ковалентных связей. На рисунке 217 изображена плоская схема пространственной решётки кристалла германия. При температуре, близкой к абсолютному нулю, ковалентные связи германия достаточно прочны, поэтому свободные электроны отсутствуют и германий является диэлектриком.
Для того чтобы разорвать ковалентную связь и сделать электрон свободным, кристаллу германия необходимо сообщить некоторую энергию, например, нагревая кристалл или облучая его поверхность. При этом часть электронов получает энергию, достаточную для того, чтобы покинуть атомы и стать свободными.
Нейтральный атом, которому принадлежал освободившийся электрон, становится положительно заряженным ионом, а в ковалентных связях образуется вакантное место с недостающим электроном. Его называют дыркой (рис. 218).
Интересно знать:
Дырочная проводимость в действительности обусловлена «эстафетным» перемещением по вакансиям от одного атома кристалла полупроводника к другому электронов, которые осуществляют ковалентную связь. Дырок как положительных зарядов, существующих реально, в действительности нет. Тем не менее представление о них является хорошей физической моделью, которая даёт возможность рассматривать электрический ток в полупроводниках на основе законов физики.
Дырки считают подвижными носителями положительного заряда, который равен модулю заряда электрона.
При наличии внешнего электрического поля на беспорядочное движение свободных электронов и дырок накладывается их упорядоченное движение, т. е. возникает электрический ток. Причём движение свободных электронов происходит в направлении, противоположном направлению напряжённости 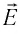
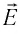
Проводимость, обусловленную движением свободных электронов и дырок в чистом полупроводнике, называют собственной проводимостью полупроводника.
Примесная проводимость полупроводников
Изменить свойства полупроводников можно не только нагреванием или воздействием электромагнитного излучения, но и добавлением в чистый полупроводник примесей. Тогда в полупроводнике наряду с собственной проводимостью возникает примесная проводимость.
Проводимость, обусловленную наличием примесей в полупроводнике, называют примесной проводимостью полупроводника.
Рассмотрим механизм этой проводимости на примере кристалла германия 
Четыре валентных электрона атома мышьяка образуют ковалентные связи с соседними атомами германия (рис. 220). Пятые электроны атомов мышьяка не задействованы в образовании ковалентных связей и могут свободно перемещаться, почти как электроны в металлическом проводнике. Проводимость такого кристалла будет преимущественно электронной. Дырки, образующиеся в результате разрыва отдельных ковалентных связей между атомами германия, являются неосновными носителями электрического заряда, так как их концентрация мала по сравнению с концентрацией свободных электронов. Такие полупроводники называют электронными полупроводниками или полупроводниками п-типа (от лат. negativ — отрицательный).
Теперь рассмотрим механизм примесной проводимости полупроводника на примере кристалла германия Ge, содержащего примесь атомов индия In, валентность которых равна трём.
Валентные электроны атома индия образуют ковалентные связи лишь с тремя соседними атомами германия (рис. 221). На образование связи с четвёртым атомом германия у атома индия электрона нет. Поэтому возле каждого атома индия одна из ковалентных связей будет незаполненной, т. е. возникает дырка. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов германия. Но при этом дырка образуется на том месте, где до этого находился электрон.
В результате введения такой примеси в кристалле разрывается множество ковалентных связей и образуются дырки. Проводимость такого кристалла будет преимущественно дырочной. Свободные электроны, которые возникают за счёт собственной проводимости полупроводника, являются неосновными носителями электрического заряда, так как их концентрация мала по сравнению с концентрацией дырок. Такие полупроводники называют дырочными полупроводниками или полупроводниками р-типа (от лат. positiv — положительный).
Техническое применение полупроводников
Приборы, работа которых основана на свойстве полупроводников изменять своё сопротивление при изменении температуры, называют термисторами или терморезисторами.
Терморезисторы (рис. 222) используют для защиты телефонных станций и линий от токовых перегрузок, для пускозащитных реле компрессоров холодильников, поджига люминесцентных ламп, подогрева дизельного топлива; в различных электронагревательных устройствах: нагревательных решётках тепловентиляторов, сушилках для обуви.
Приборы, работа которых основана на свойстве полупроводников изменять своё сопротивление при изменении освещённости их поверхности, называют фоторезисторами или фотосопротивлениями (рис. 223). Их используют для регистрации слабых потоков света, при сортировке и счёте готовой продукции, для контроля качества и готовности самых различных деталей; в полиграфической промышленности для обнаружения обрывов бумажной ленты, контроля количества листов бумаги, подаваемых в печатную машину; в медицине, сельском хозяйстве и других областях.
Широкое применение находят полупроводниковые диоды, которые являются основными элементами выпрямителей переменного тока и детекторов электромагнитных сигналов. С помощью полупроводниковых диодов можно осуществить непосредственное превращение энергии электромагнитного излучения в электрическую энергию. Такие диоды называют фотодиодами (рис. 224).
В электрических устройствах (схемах) используют транзистор — прибор, предназначенный для усиления, генерации, преобразования и коммутации сигналов в электрических цепях.
Светоизлучающий диод (светодиод) — это полупроводниковый прибор, преобразующий электрическую энергию непосредственно в световое излучение. Он представляет собой миниатюрный полупроводниковый диод, помещённый в прозрачный корпус (рис. 225). Используя светодиоды, изготавливают, например, светодиодные светильники (рис. 226).
Из истории физики:
В 2000 г. уроженцу Беларуси Жоресу Ивановичу Алфёрову (1930-2019) совместно с американскими учёными Гербертом Кремером и Джеком Килби была присуждена Нобелевская премия по физике за «исследование полупроводниковых гетероструктур, лазерных диодов и сверхбыстрых транзисторов».
Обобщение и систематизация знаний:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Электростатика
- Закон сохранения заряда в физике
- Электрическое поле заряженного шара
- Электрические явления в физике
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Изменение агрегатного состояния вещества
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Эбоненок. Электродинамика. ЕГЭ по физике 2024 | Саня ЭбонитСкачать

Магнитное поле в веществе. Теорема о циркуляции векторов В и H
Для количественного описания намагничивания магнетиков вводят векторную величину — намагниченность, определяемую магнитным моментом единицы объема магнетика:
где рт = ? Д, — магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул [см. (62.7)].
В веществе на магнитное поле макротоков (в частности, токов проводимости) накладывается магнитное поле, создаваемое намагниченным веществом (магнитное поле микротоков). Следовательно, вектор магнитной индукции результирующего магнитного поля в магнетике равен векторной сумме магнитных индукций внешнего
поля Ва (создаваемого намагничивающим током в вакууме) и поля микротоков В’ (создаваемого молекулярными токами):
Запишем выражение для циркуляции [см. (58.1)| поля (64.1):
Согласно формуле (58.2),
где I — алгебраическая сумма макротоков (токов проводимости), охватываемых замкнутым контуром, по которому производится интегрирование.
Для поля микротоков должно выполняться такое же соотношение
где Г — алгебраическая сумма микротоков (молекулярных токов), охватываемых тем же замкнутым контуром L.
Подставив формулы (64.3) и (64.4) в выражение (64.2), получим
т. е. циркуляция вектора магнитной индукции В по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Выражение (64.5) — закон полного тока для магнитного
поля в веществе (теорема о циркуляции вектора В)
|является обобщением закона (58.2)).
Таким образом, вектор В характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнетиках, поэтому линии вектора магнитной индукции В не имеют источников и являются замкнутыми.
Из теории известно, что циркуляция намагниченности J по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:
Тогда закон полного тока для магнитного поля в веществе (64.5) можно записать в виде
Циркуляция величин, стоящих в скобках под знаком интеграла, определяется только макроскопическими токами. Вектор
называют напряженностью магнитного пом.
Учитывая формулу (64.8), выражение (64.7) запишется в виде
т. е. циркуляция вектора Н по произвольному неподвижному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром. Выражение (64.9) представляет собой теорему о циркуляции вектора Н.
Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и //) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смешения D является вектор напряженности Н магнитного поля.
В случае вакуума J = 0, поэтому
и формула (64.9) переходит в формулу (58.2).
Из формулы (64.10) можно определить единицу напряженности магнитного поля в СИ — ампер на метр (А/м): I А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4л • 10
Как показывает опыт, в несильных полях намагниченность пропорциональна напряженности поля, вызывающего намагничивание, т. е.
где х — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнетиков х отрицательна (поле молекулярных токов противоположно внешнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).
Используя формулу (64.11), выражение (64.8) можно записать в виде
называют магнитной проницаемостью вещества.
Согласно формулам (64.12) и (64.13), можем записать, что
Так как абсолютное значение магнитной восприимчивости для диа- и парамагнетиков очень мало (порядка 10 4 —КТ 6 ), то для них ц незначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков % 0 и р > I.
📺 Видео
Линейная электродинамикаСкачать

Физика - Магнитное полеСкачать

ВСЁ ЭЛЕКТРИЧЕСТВО ЗА 8 ЧАСОВ С НУЛЯ I Физика ОГЭ ЕГЭ 2024 I Эмиль Исмаилов - Global_EEСкачать

Электростатика с нуля за 1 час | физика, подготовка к ЕГЭ | 10, 11 классСкачать

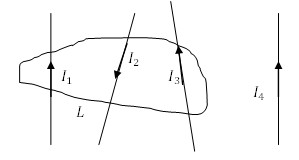

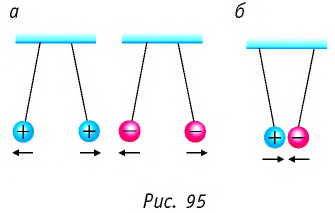
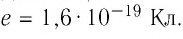
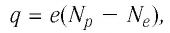
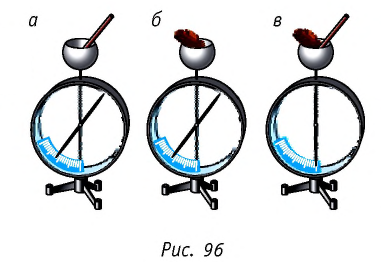

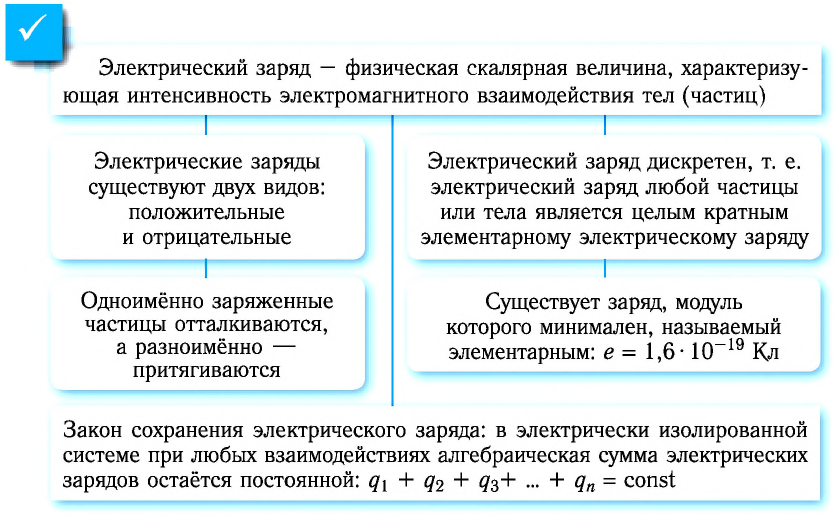
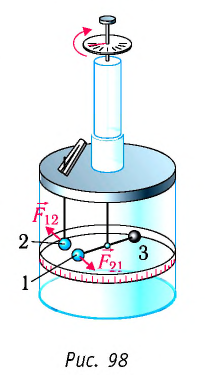
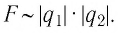

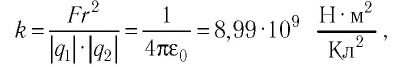
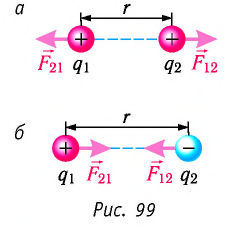
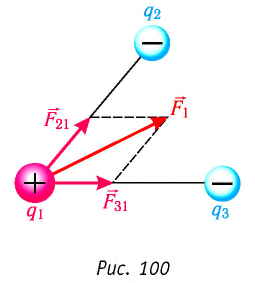
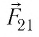
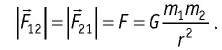

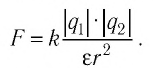

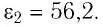
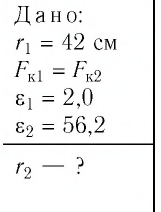
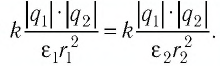
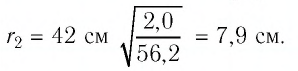
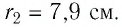

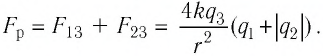
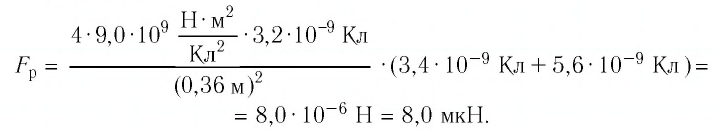
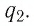
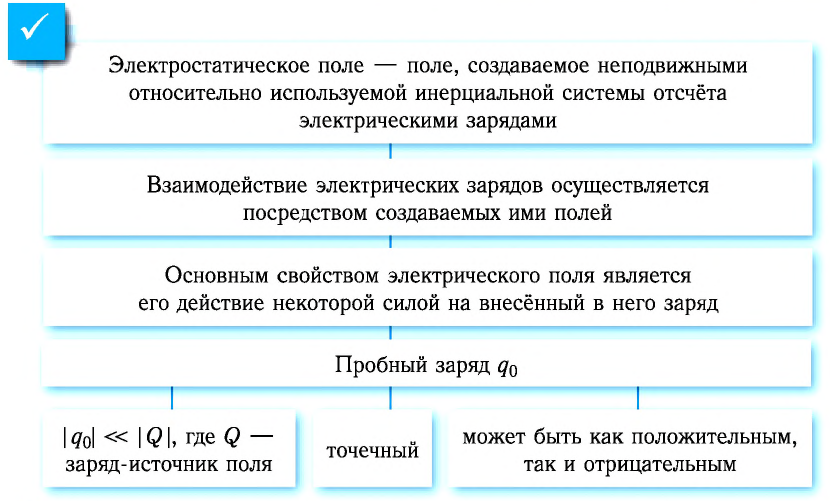
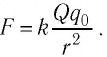


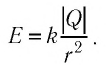
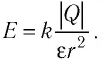
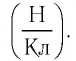
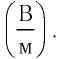
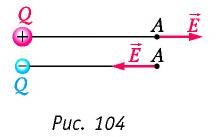
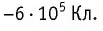

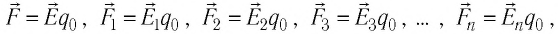
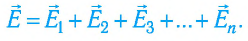
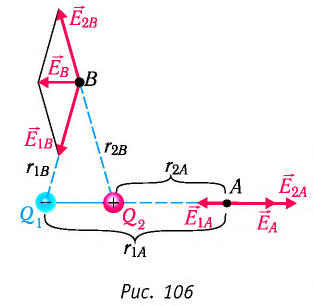


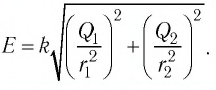
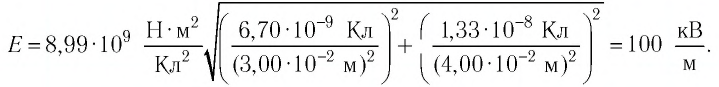
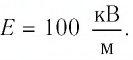
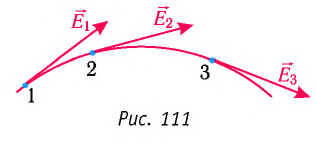
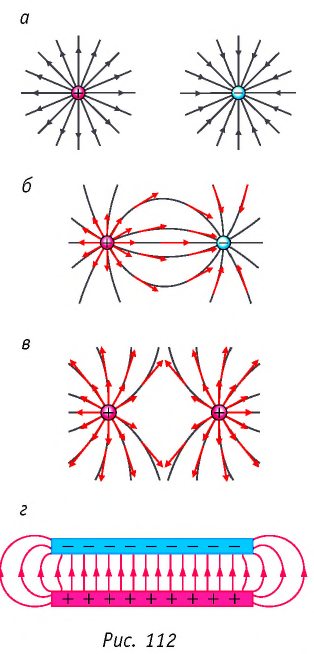
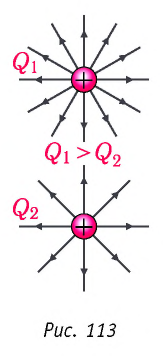
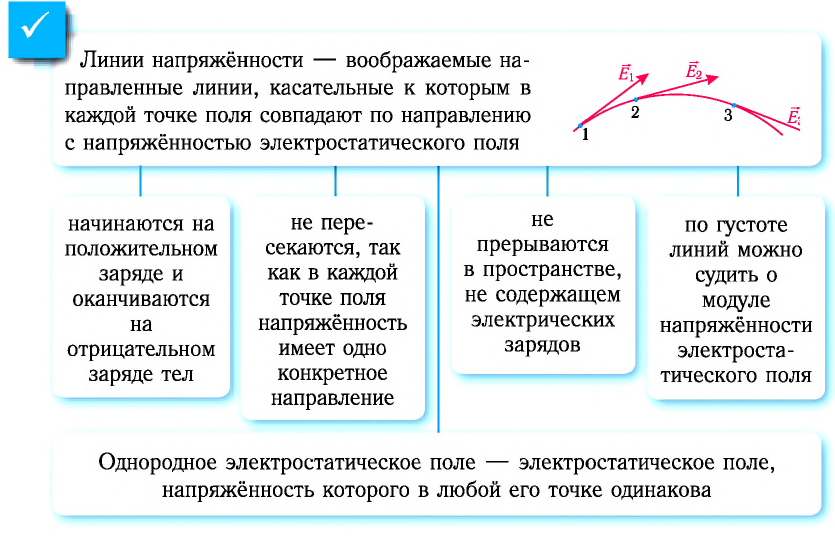
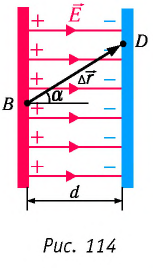

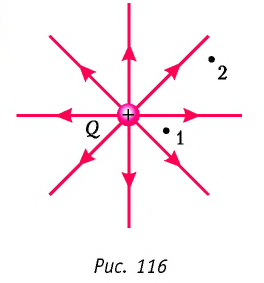
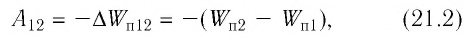



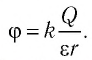
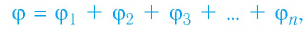

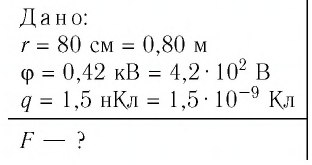


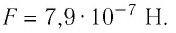
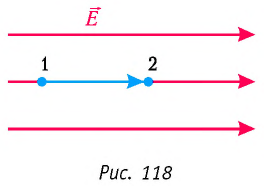
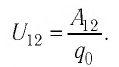
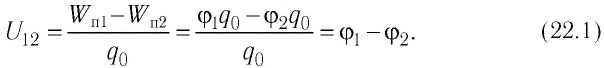
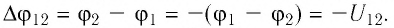
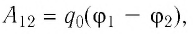
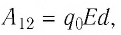


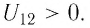
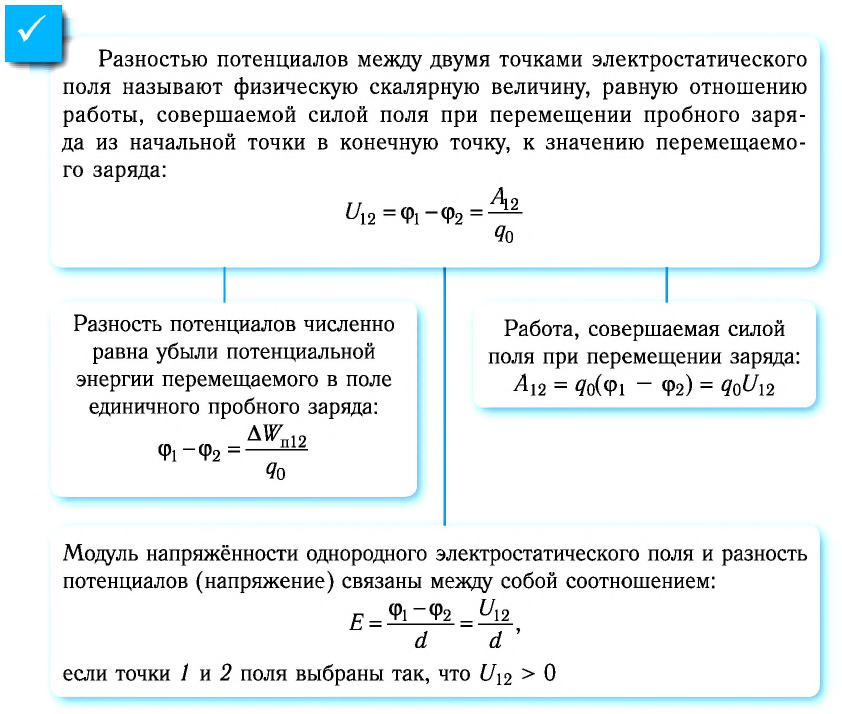
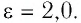
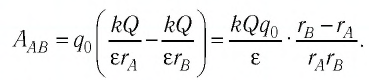
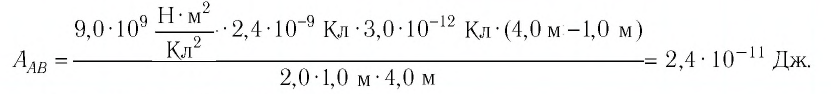
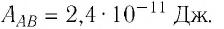
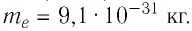
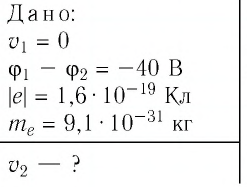
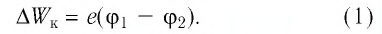
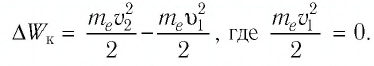
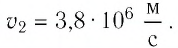
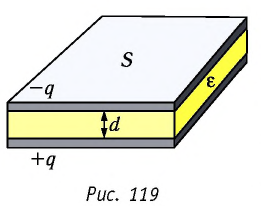
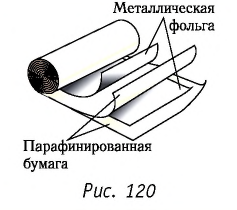

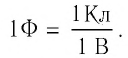
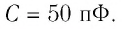
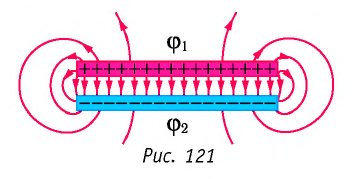
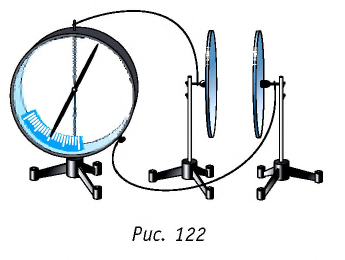
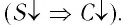
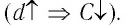
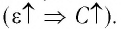
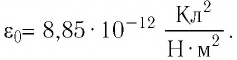
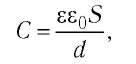
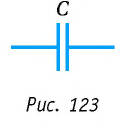
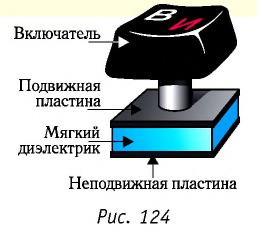
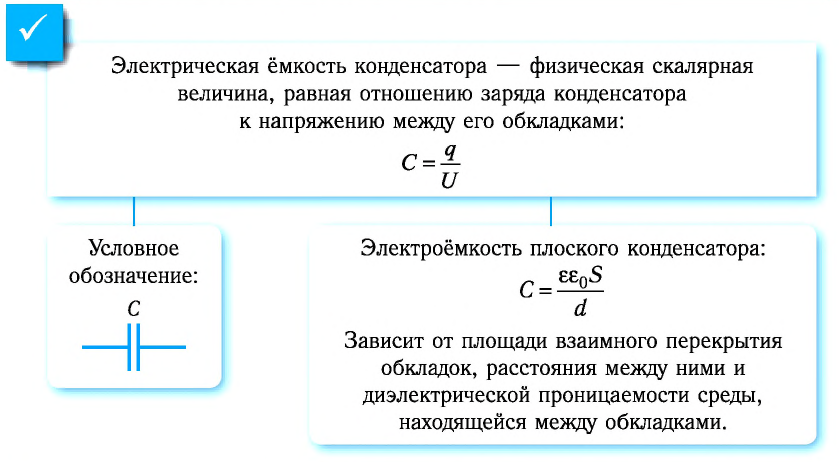
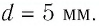
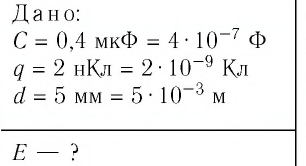
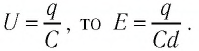
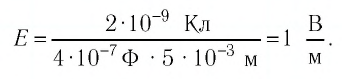
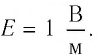
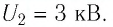
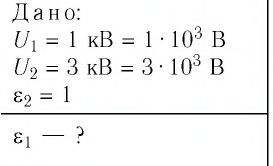
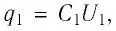


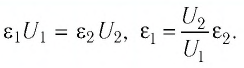
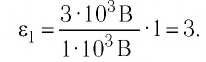
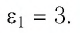
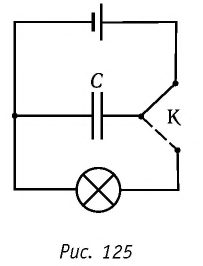
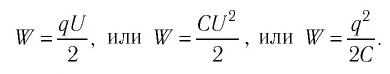
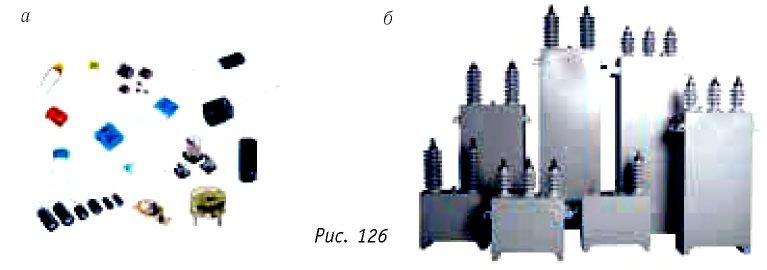
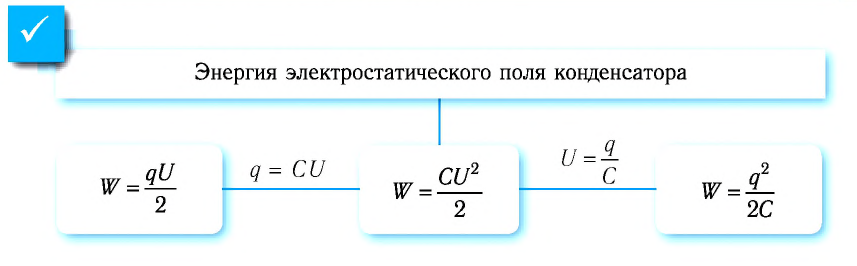
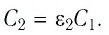
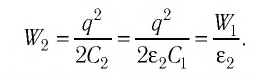
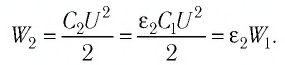
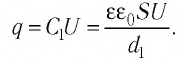
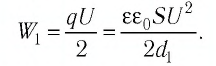
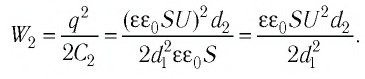
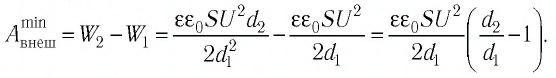
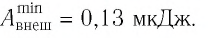
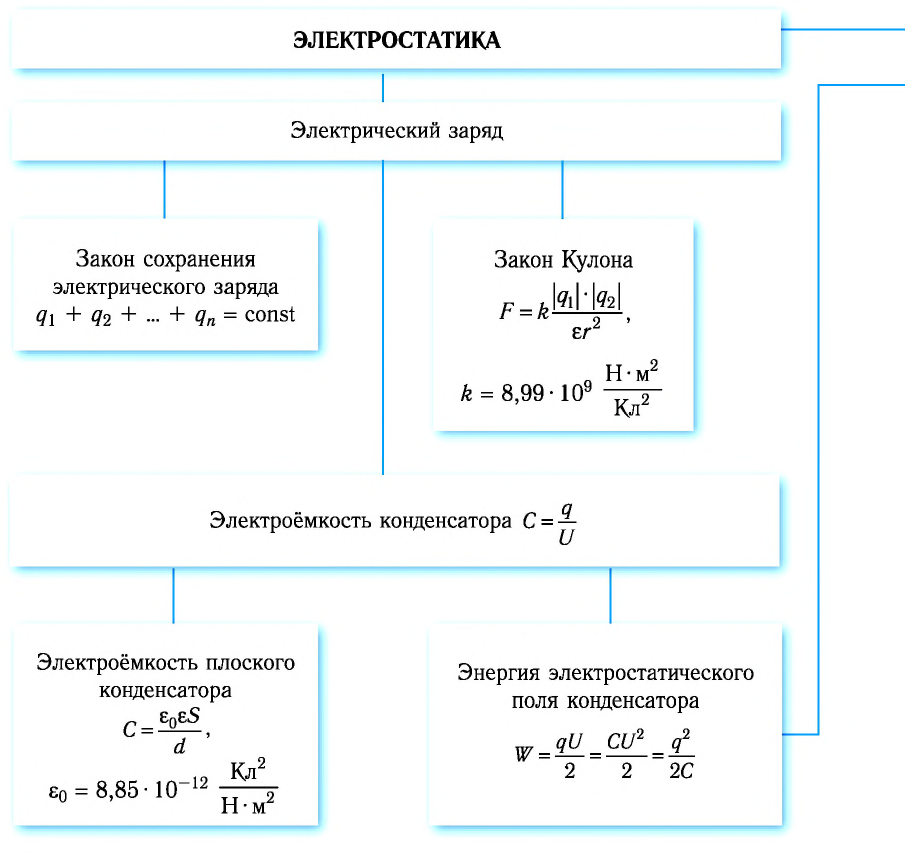
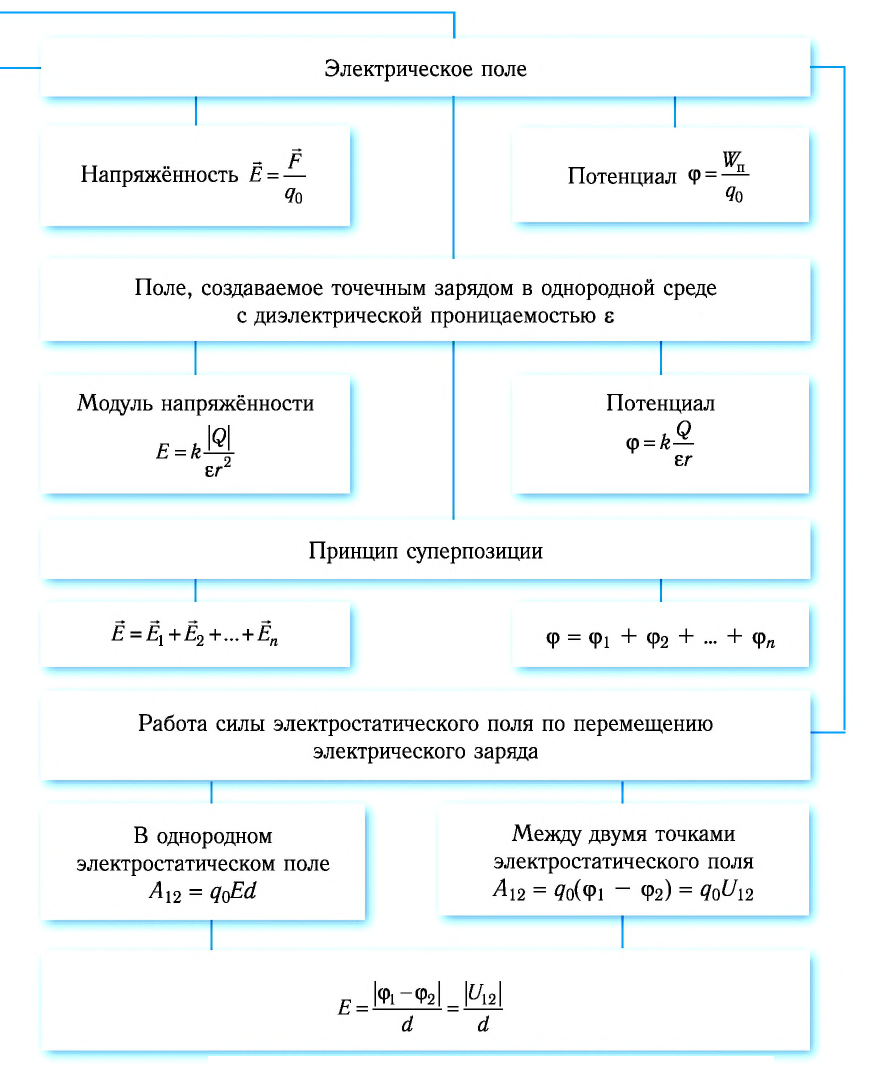
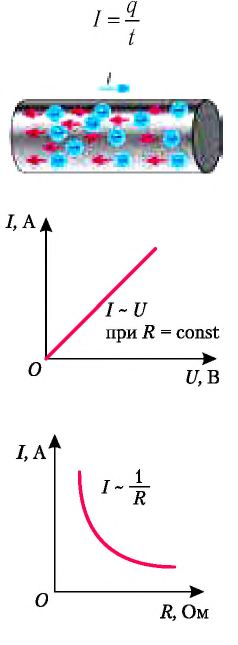
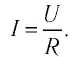
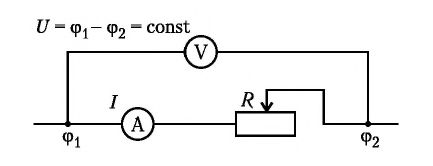
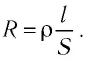
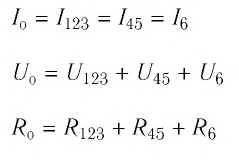
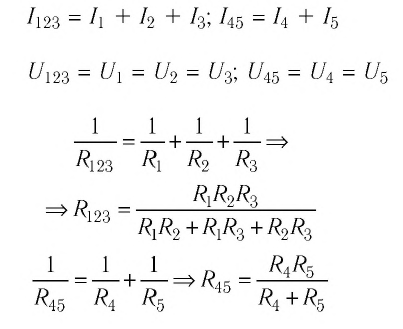
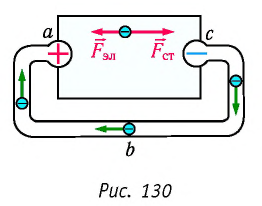

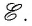

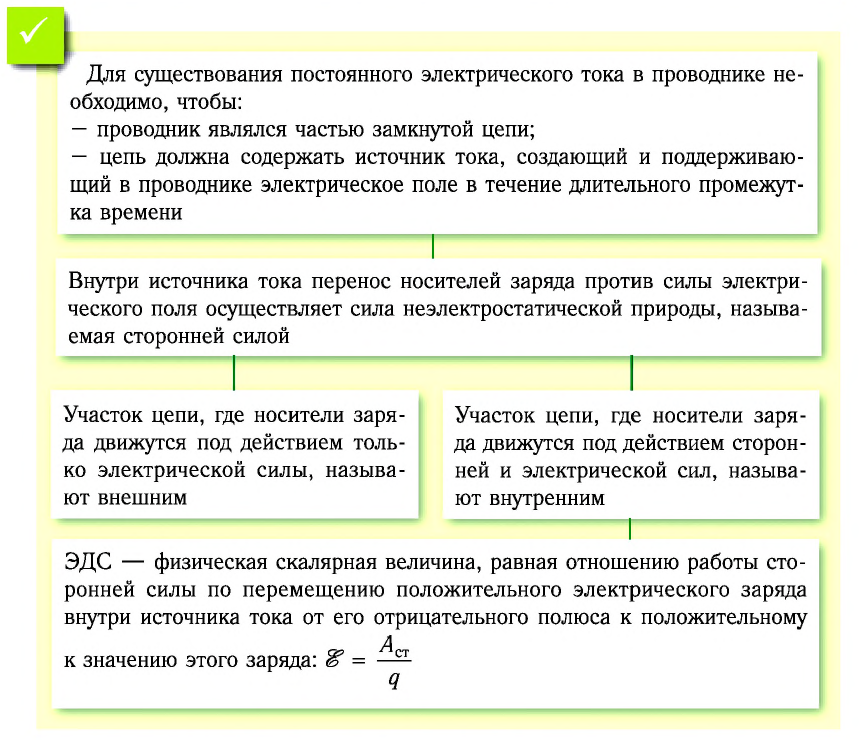
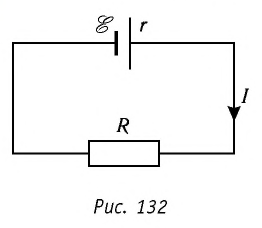
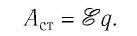





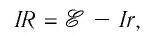

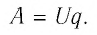
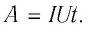
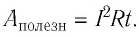
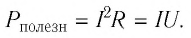
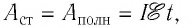
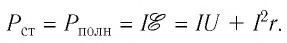
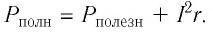
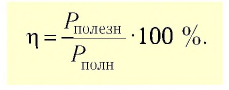
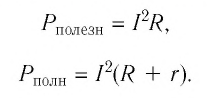
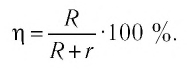
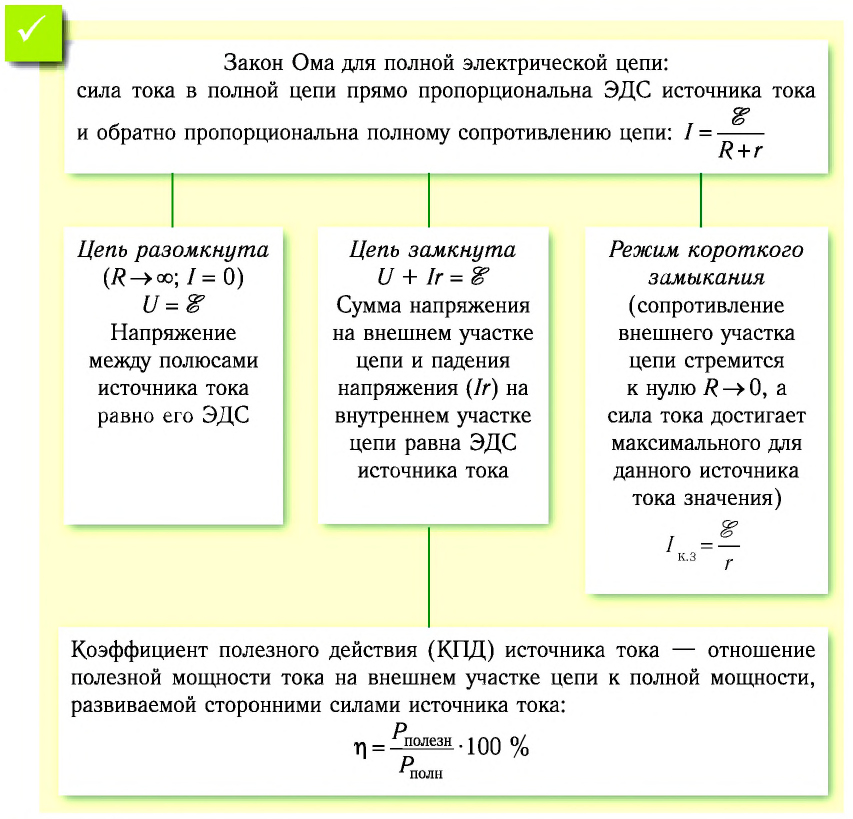

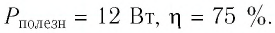
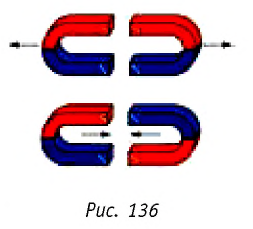
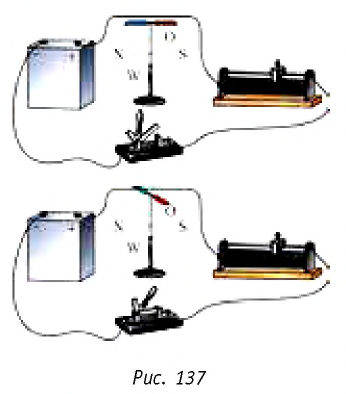
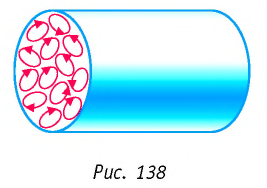
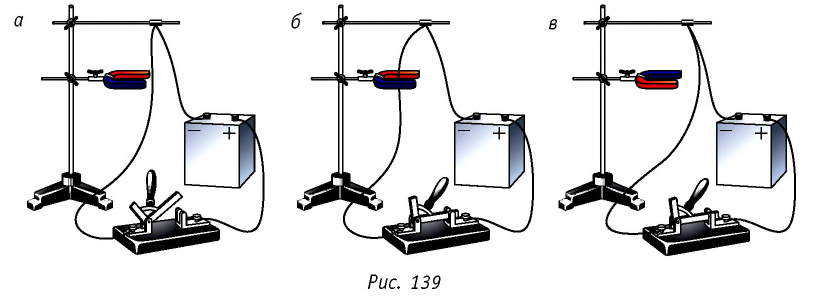
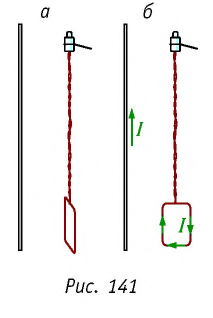


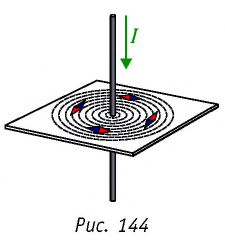
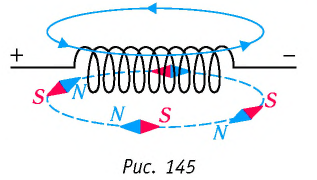
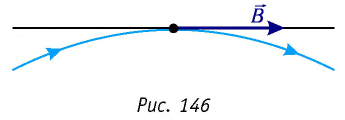
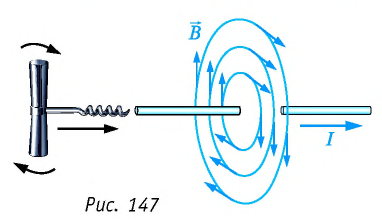

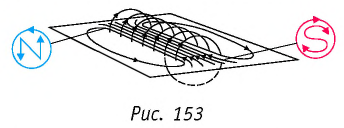
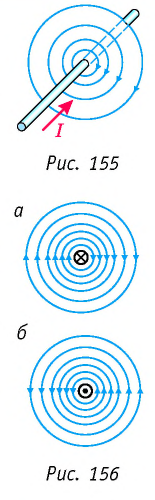
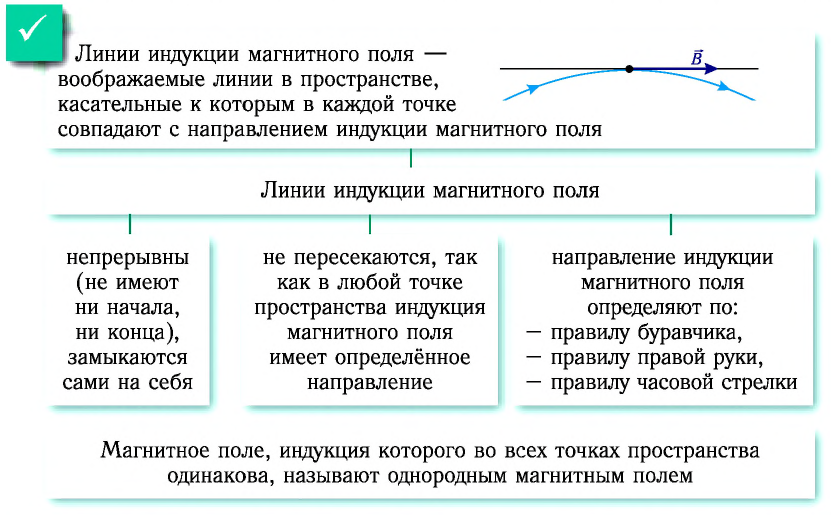
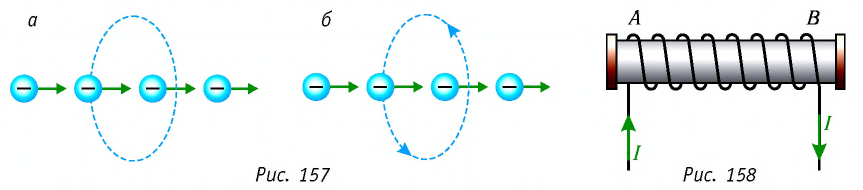
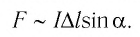

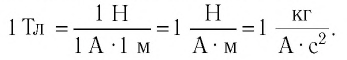
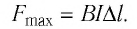

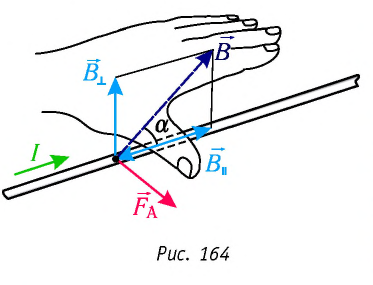


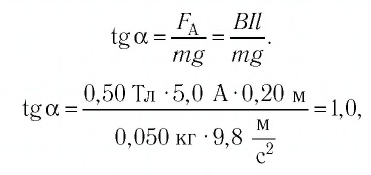
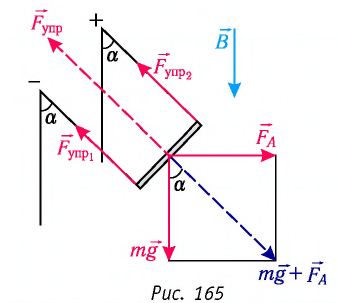
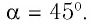
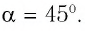
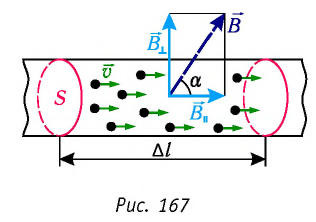
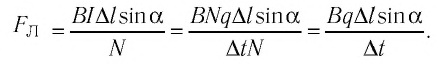

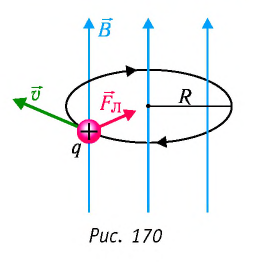
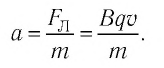
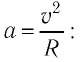
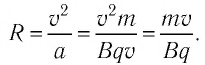
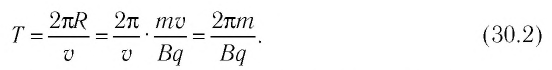
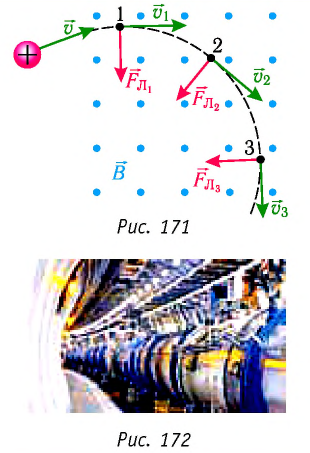

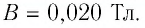
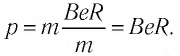
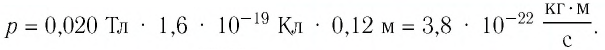
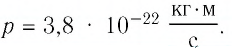
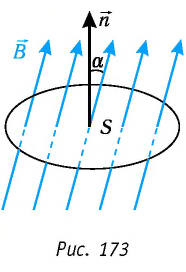

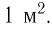
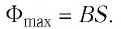
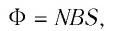
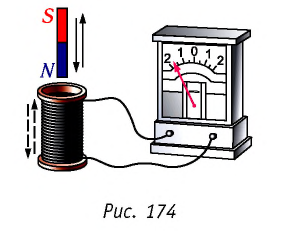
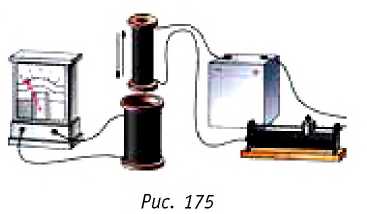
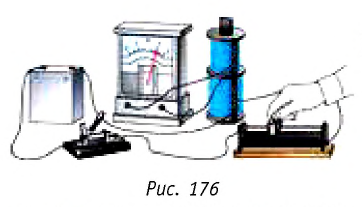
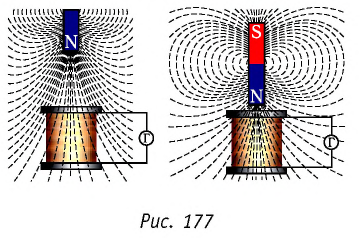
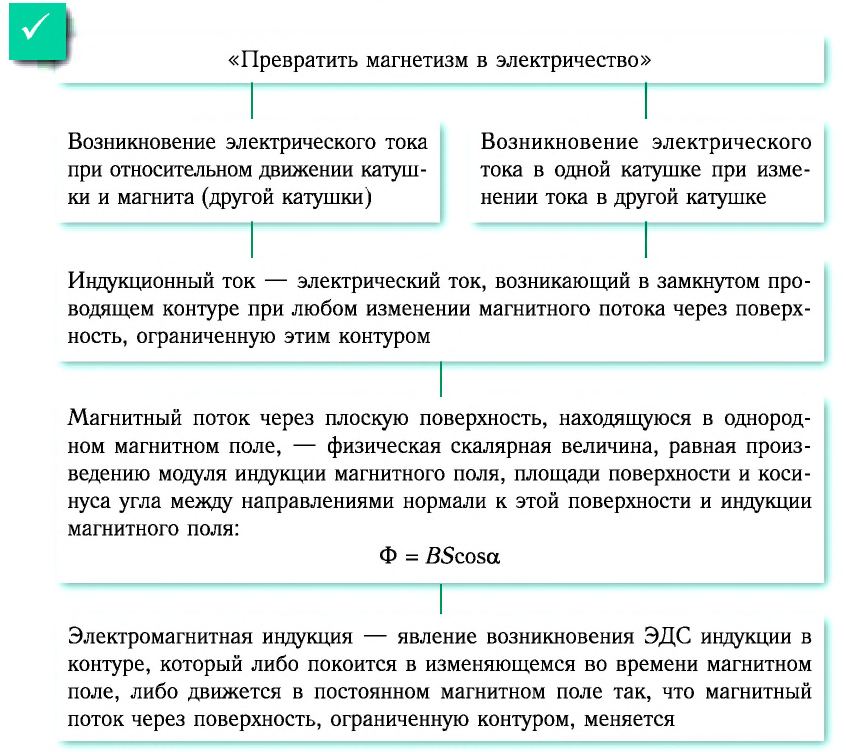
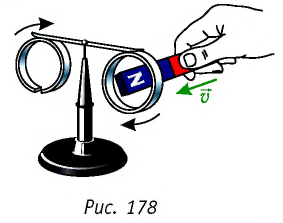
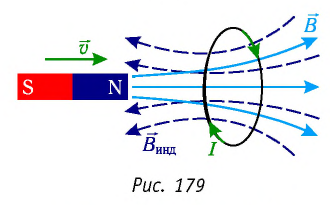
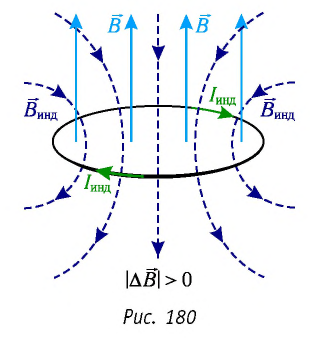
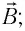
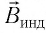 : если приращение магнитного потока
: если приращение магнитного потока 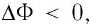 то направления индукций внешнего магнитного поля
то направления индукций внешнего магнитного поля 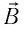 и магнитного поля индукционного тока
и магнитного поля индукционного тока 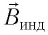 совпадают, если
совпадают, если 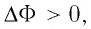 то — противоположны;
то — противоположны;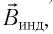 по правилу буравчика (правилу часовой стрелки) определить направление индукционного тока.
по правилу буравчика (правилу часовой стрелки) определить направление индукционного тока.