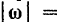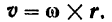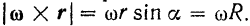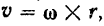Вектор мгновенной угловой скорости это

Видео:Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Определение и формула угловой скорости

Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.

Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.

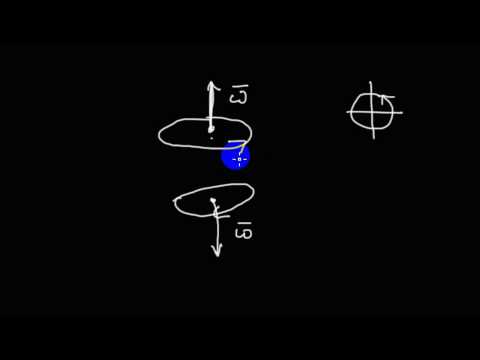
Перемещение при вращении характеризуют при помощи угла поворота $(varphi)$ . Часто используют вектор элементарного поворота $bar$ , который равен по величине элементарному углу поворота тела $(d varphi)$ за маленький отрезок времени dt и направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.

Угловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой $omega$ . Математически определение угловой скорости записывают так:

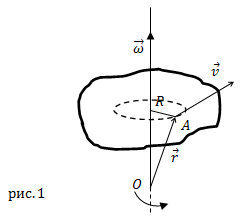
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).

Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($bar$ при этом изменяет направление).

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Равномерное вращение

Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:

где $(varphi)$ – угол поворота, t – время, за которое этот поворот совершён.

Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($Delta varphi=2 pi$). Угловая скорость связана с периодом обращения как:

С числом оборотов в единицу времени ($nu) угловая скорость связана формулой:

Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.

Видео:Механика | кинематика на плоскости | движение по окружности | вектор угловой скоростиСкачать

Формула, связывающая линейную и угловую скорости

Линейная скорость $bar$ точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:

где $bar$ – перпендикулярная к оси вращения компонента радиус-вектора точки $A (bar)$ (рис.1). Вектор $bar$ проводят от точки, находящейся на оси вращения к рассматриваемой точке.

Видео:угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать

Единицы измерения угловой скорости

Основной единицей измерения угловой скорости в системе СИ является: [$omega$]=рад/с

В СГС: [$omega$]=рад/с

Видео:Мгновенный центр вращенияСкачать

Примеры решения задач

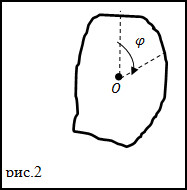
Задание. Движение тела с неподвижной осью задано уравнением $varphi=2 t-4 t^$, $(varphi)$ в рад, t в сек. Начало вращения при t=0 c. Положительным считают углы указанные направлением стрелки (рис.2). В каком направлении ( относительно часовой стрелки поворачивается тело) в момент времени t=0,5 c.

Решение. Для нахождения модуля угловой скорости применим формулу:

Используем заданную в условии задачи функцию $varphi(t)$, возьмем производную от нее по времени, получим функцию $omega(t)$:

Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):

Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.

Видео:Средняя и мгновенная скоростиСкачать

Угловая скорость тела как вектор

Угловая скорость тела как вектор. Выражение скорости точки тела в виде векторного произведения. Понятие о свободном движении твердого тела

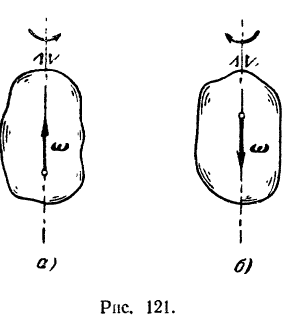
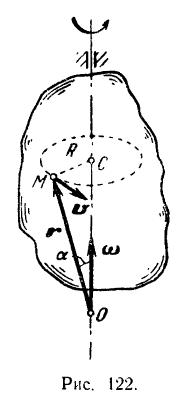
Вектором угловой скорости тела называется вектор, направленный вдоль оси вращения так, чтобы, смотря с конца его, мы видели вращение тела совершающимся против хода стрелки часов (рис. 121, а и б).

Вектор есть вектор скользящий, т. е. за его начало можно взять любую точку, лежащую на оси вращения тела.

В случае вращения тела вокруг неподвижной оси модуль этого вектора равен абсолютному значению производной от угла поворота тела по времени .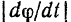

Задание вектора угловой скорости полностью определяет вращательное движение тела, так как позволяет знать положение оси вращения тела, сторону вращения и численное значение угловой скорости.

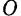
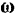
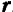
Отложим на оси вращения из какой-либо произвольной ее точки вектор угловой скорости тела и из этой же точки проведем радиус-вектор , определяющий положение данной точки тела (рис. 122).

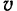
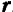
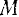
Вспоминая еще раз (стр. 62) понятие о векторном произведении двух векторов, мы придем к выводу, что скорость любой точки вращающегося твердого тела равна векторному произведению вектора угловой скорости тела на радиус-вектор данной точки (если за начало этого радиуса-вектора взята точка на оси вращения тела):

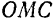
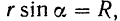
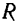
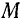
В самом деле, из прямоугольного треугольника будем иметь , где — расстояние точки до оси вращения. Модуль векторного произведения

Направлен же вектор

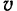
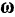
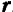
так же как и вектор , перпендикулярно к плоскости и в сторону вращения тела, т. е. в сторону, откуда кратчайший переход от к будет представляться совершающимся против хода стрелки часов.

Любое движение свободного твердого тела, как это доказывается в более полных курсах механики, можно считать составленным из двух движений: поступательного движения со скоростью произвольно выбранной точки тела (полюса) и вращательного движения вокруг некоторой оси, проходящей через выбранный полюс.

Каждому моменту времени (мгновению) соответствует свое положение этой оси в пространстве и относительно данного тела, и поэтому, в отличие от неподвижной оси, она называется мгновенной осыо вращения тела.

Угловая скорость вращения тела вокруг мгновенной оси называется мгновенной угловой скоростью.

Мгновенную угловую скорость тела, как и в случае вращения тела вокруг неподвижной оси, можно представить в виде вектора, направленного вдоль мгновенной оси. Вследствие непрерывного изменения положения мгновенной оси, вектор 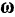мгновенной угловой скорости изменяется со временем не только по абсолютной величине, по и по направлению.

Скорости точек тела, лежащих на мгновенной оси, равны нулю. Отсюда следует, что скорости любых точек тела при его вращении вокруг мгновенной оси можно вычислять в каждый данный момент времени по установленной выше формуле (91)

где 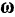— соответствующий данному моменту времени вектор мгновенной угловой скорости тела и — радиус-вектор точки, имеющий начало на мгновенной оси вращения.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Магия тензорной алгебры: Часть 6 — Кинематика свободного твердого тела. Природа угловой скорости

Видео:Мгновенная скорость (видео 6) | Векторы. Прямолинейное движение | ФизикаСкачать

Введение

Что такое угловая скорость? Скалярная или векторная величина? На самом деле это не праздный вопрос.

Читая лекции по теоретической механике в университете, я, следуя традиционной методике изложения курса кинематики, вводил понятие угловой скорости в теме «Скорость точки тела при вращательном движении». И там угловая скорость впервые появляется как скалярная величина, со следующим определением.

Угловая скорость твердого тела — это первая производная от угла поворота тела по времени

А вот потом, при рассмотрении каноничной формулы Эйлера для скорости точки тела при вращении

Угловая скорость тела — это псевдовектор, направленный вдоль оси вращения тела в ту сторону, откуда вращение выглядит происходящим против часовой стрелки

Ещё одно частное определение, которое, во-первых, утверждает неподвижность оси вращения, во-вторых навязывает рассмотрение лишь правой системы координат. И наконец термин «псевдовектор» обычно объясняется студентам так: «Посмотрите, ведь мы показали, что омега — скалярная величина. А вектор мы вводим для того, чтобы выписать формулу Эйлера».

При рассмотрении сферического движения оказывается потом, что ось вращения меняет направление, угловое ускорение направлено по касательной к годографу угловой скорости и так далее. Неясности и вводные допущения множатся.

Учитывая уровень подготовки школьников, а так же вопиющую глупость, допускаемую в программах подготовки бакалавров, когда теормех начинается с первого (вдумайтесь!) семестра, такие постепенные вводные, на палках, веревках и желудях наверное оправданы.

Но мы с вами заглянем, что называется, «под капот» проблемы и, вооружившись аппаратом тензорного исчисления, выясним, что угловая скорость — это псевдовектор, порождаемый антисимметричным тензором второго ранга.

Думаю для затравки вполне достаточно, а поэтому — начнем!

Видео:Кугушев Е. И. - Классическая механика - Мгновенная угловая скорость твердого тела, формула ЭйлераСкачать

1. Свободное движение твердого тела. Тензор поворота

Если движение, совершаемо телом не ограничено связями, то такое его движение называют свободным

Это — самый общий случай движения тела. Следующий рисунок иллюстрирует тот факт, что свободное движение тела можно представить как сумму двух движений: поступательного вместе с полюсом и сферического вокруг полюса.

Рис. 1. Обычная иллюстрация из курса теоретической механики: определение положения свободного твердого тела в пространстве.

Напомню, что речь идет об абсолютно твердом теле, то есть теле, расстояния между точками которого не изменяется с течением времени. Ещё можно сказать, что твердое тело представляет собой неизменяемую механическую систему.

Как видно из рисунка 1, обычной практикой является рассмотрение двух систем координат — одна считается неподвижной и называется базовой, другая жестко связанна с телом и поворачивается относительно базовой вместе с ним. Такую систему координат называют связанной.

Сначала я тоже хотел ограничиться декартовыми координатами. Но тогда бы мои читатели задали бы мне логичный вопрос — «а зачем тогда тут тензоры?». Поэтому, потратив четыре для в мучительных раздумьях и «нагуляв» окончательное решение пару часов назад, я решил замахнуться на «Вильяма, нашего, Шекспира» и изложить дальнейшие рассуждения в криволинейных координатах.

Рис. 2. Ориентация твердого тела в локальном базисе.

Пусть положение полюса задается вектором

Причем под этим вектором не следует понимать радиус-вектор, так как в криволинейных координатах такое понятие бессмысленно.

В точке O₁ задан локальный репер базовой системы координат, образованный тройкой векторов . С движущимся телом связан подвижный репер . Поворот связанного репера относительно базового можно задать линейным оператором. Получим этот оператор и исследуем его свойства

Рассмотрим некоторую точку M, принадлежащую телу. К ней из полюса можно провести вектор неподвижный относительно связанного репера. Его можно разложить по векторам этого репера

и по векторам базового репера

Каждый вектор связанного репера можно разложить через векторы базового репера

Подставляем (4) в (2) и сравниваем с (3)

Из (5) понятно, что компоненты вектора в базовой системе координат, пересчитываются через его компоненты в связанной системе путем применения линейного оператора

или в безиндексной форме

где столбцы матрицы

– контравариантные компоненты векторов связанного репера по отношению к базовому. Точка, как мы уже отмечали в прошлой статье, обозначает умножение тензоров с последующей сверткой по соседней паре индексов. Линейный оператор

действует на векторы таким образом, что поворачивает их относительно некоторой оси, не меняя длины и угла между векторами. Такое преобразование пространства называется ортогональным. Для того, чтобы таковое преобразование было возможным, оператор (7) должен обладать вполне определенными свойствами. Если длина векторов базиса и углы между ними не меняются, то это означает равенство всех попарных скалярных произведений векторов репера как в базовой, так и в связанной системах координат

Правая часть (8) — это локальный метрический тензор

Преобразование координат при повороте является тождественным для метрического тензора, то есть переводит метрический тензор сам в себя.

В выражении (10) нетрудно увидеть преобразование метрического тензора про смене системы координат, о котором мы подробно говорили в самой первой статье цикла

Стоп! Но мы же знаем, что матрицы поворота обычно ортогональны, то есть произведение матрицы поворота на её транспонированную дает единичную матрицу, иными словами, чтобы обратить матрицу поворота её достаточно транспонировать.

Но ортогональность свойственна матрицам поворота, преобразующим ортонормированный декартов базис. Здесь мы имеем дело с локальным базисом, при повороте которого должны сохранятся длины векторов и углы между ними. Если мы примем базис декартовым, то из (10) мы получим привычные свойства матрицы поворота, к примеру её ортогональность.

Для дальнейших вычислений нам потребуется знать, как будет выглядеть матрица обратного преобразования, то есть . Что же, посмотрим. Для этого умножим (10) слева на и справа на

откуда незамедлительно получаем

Выходит, что матрица обратного преобразования действительно получается из транспонированной матрицы преобразования, но с участием метрического тензора. Выражения (10) и (11) очень пригодятся нам, а пока сделаем некоторые выводы.

Закон свободного движения твердого тела можно выписать в криволинейных координатах в виде системы уравнений

При этом (12) — закон движения полюса, а (13) — закон сферического движения тела вокруг полюса. При этом (13) — тензор ранга (1,1), называемый тензором поворота.

Видео:Мгновенная скоростьСкачать

2. Скорость точки тела при свободном движении. Угловая скорость выходит на сцену

Вычислим скорость точки M, положение которой в связанной системе координат задается постоянными, в силу твердости тела, криволинейными координатами

Из курса теоретической механики известна формула, определяющая скорость точки тела в данном движении

где — скорость полюса; — скорость точки вокруг полюса.

Так как все координаты, кроме (13) определены относительно базового репера, мы можем записать

Индекс в круглых скобках означает систему координат, в которой берутся компоненты (0 — базовая, 1 — связанная). Дифференцируем (15) по времени с учетом (13)

Перейдем в (16) к связанной системе координат, домножив (15) слева на

где — компонента оператора обратного преобразования .

Теперь сравним (17) и (14). В последнем слагаемом должно вылезти векторное произведение. Вспоминая определение векторного произведения через тензор Леви-Чивиты, данное во второй статье цикла, замечаем, что на выходе оно дает ковектор, поэтому в (17) перейдем к ковариантым компонентам, домножив это выражение на метрический тензор слева

Теперь представим себе, как выглядел бы ковектор скорости точки относительно плюса, записанный через вектор угловой скорости

🎬 Видео

Лекция 10. Угловая скорость и угловое ускорение │Физика с нуляСкачать

Соотношение угловой скорости и линейной скоростиСкачать

Мгновенный центр скоростейСкачать

Урок 24. Мгновенная скорость. Равноускоренное движение. УскорениеСкачать

Линейная и угловая скорости при равномерном движении по окружностиСкачать

Лекция 6.2 | Угловая и линейная скорость | Александр Чирцов | ЛекториумСкачать

Угловая скорость и радианная мера углаСкачать

Мгновенная скорость. Сложение скоростей | Физика 10 класс #4 | ИнфоурокСкачать

Урок 102. Метод мгновенных осейСкачать

Механика | средняя и мгновенная скорости | 1Скачать