Как найти периметр призмы — Рецепты
- Содержание
- Что такое призма?
- Периметр призмы
- Зачем нужно рассчитывать периметр призмы?
- Пример задачи: периметр прямоугольной призмы
- Призма
- Призма
- Формулы вычисления объема и площади поверхности призмы:
- В основании лежит треугольник.
- В основании лежит четырехугольник
- 1. Прямоугольник
- 2. Ромб
- 3. Трапеция
- Рассмотрим площади правильных многоугольников:
- Подобие треугольников
- Прямоугольный треугольник и его свойства:
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
- Треугольная призма все формулы и примеры задач
- Определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Пример призмы
- Задачи на расчет треугольной призмы
- 📹 Видео
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Содержание
Вы можете видеть призмы как на уроках математики, так и в повседневной жизни. Кирпич — это прямоугольная призма. Коробка апельсинового сока — это разновидность призмы. Коробка для салфеток представляет собой прямоугольную призму. Сараи представляют собой разновидность пятиугольной призмы. Пентагон — это пятиугольная призма. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.
Призмы по определению являются твердыми объектами с одинаковыми формами концов, одинаковыми поперечными сечениями и плоскими боковыми гранями (без кривых). И хотя большинство математических задач и реальных примеров расчета призм связаны с формулой объема или формулой площади поверхности, есть одно вычисление, которое вам необходимо понять, прежде чем вы сможете это сделать: периметр призмы.
Видео:Геометрия Найдите площадь боковой поверхности правильной треугольной призмы, описанной околоСкачать

Что такое призма?
Общее определение призмы — это трехмерная сплошная форма, которая имеет следующие характеристики:
- Это многогранник (то есть это прочная фигура).
- В поперечное сечение объекта одинакова по всей длине объекта.
- Это параллелограмм (4-сторонняя форма, в которой противоположные стороны параллельны друг другу).
- Лица объекта плоский (без изогнутых граней).
- Две конечные формы идентичный.
Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольным основанием называется треугольной призмой. Призма с прямоугольным основанием называется прямоугольной призмой. Этот список можно продолжить.
Если посмотреть на характеристики призм, это исключает сферы, цилиндры и конусы как призмы, поскольку они имеют изогнутые грани. Это также исключает пирамиды, потому что они не имеют одинаковых форм основания или одинаковых поперечных сечений.
Видео:Площадь поверхности призмы. 11 класс.Скачать

Периметр призмы
Говоря о периметре призмы, вы на самом деле имеете в виду периметр базовой формы. Периметр основания призмы такой же, как и периметр вдоль любого поперечного сечения призмы, поскольку все поперечные сечения одинаковы по длине призмы.
Периметр измеряет сумму длин любого многоугольника. Итак, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.
Например, формула для нахождения периметра треугольной призмы будет представлять собой сумму трех длин треугольника, составляющего основу, или:
Периметр треугольника = a + b + c где а, б а также c — три длины треугольника.
Это будет периметр прямоугольной призмы по формуле:
Периметр прямоугольника: 2l + 2w где л — длина прямоугольника и ш это ширина.
Примените стандартные вычисления периметра к базовой форме призмы, и это даст вам периметр.
Видео:10 класс, 30 урок, ПризмаСкачать

Зачем нужно рассчитывать периметр призмы?
Определение периметра призмы не кажется слишком сложным, если вы понимаете, о чем вас спрашивают. Однако периметр — важный расчет, который учитывается в формулах площади поверхности и объема для некоторых призм.
Например, это формула для определения площади поверхности правой призмы (правая призма имеет одинаковые основания и стороны, все прямоугольные):
Площадь поверхности = 2b + ph
где b равно площади основания, p равно периметру основания, а h равно высоте призмы. Вы можете видеть, что периметр необходим для определения площади поверхности.
Видео:ЕГЭ-2020 по математике: площадь боковой поверхности треугольной призмыСкачать

Пример задачи: периметр прямоугольной призмы
Допустим, вам задали задачу с правильной прямоугольной призмой и попросили определить ее периметр. Вам даны следующие значения:
Чтобы найти периметр, используйте формулу для определения периметра прямоугольной призмы, так как название говорит вам, что основание — прямоугольник:
Периметр = 2l + 2w = 2 (75 см) + 2 (10 см) = 150 см + 20 см = 170 см
Затем вы можете найти площадь поверхности, потому что вам дана высота, у вас есть периметр основания и дано, что эта призма является право призма.
Площадь основания равна длине × ширине (как всегда для прямоугольника), что составляет:
Площадь основания = 75 см × 10 см = 750 см 2
Теперь у вас есть все значения для расчета площади поверхности:
Площадь поверхности = 2b + ph = 2 (750 см 2 ) + 170 см (5 см) = 1500 см 2 + 850 см = 2350 см 2
Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Призма
Видео:Нахождение площади поверхности треугольной призмы при помощи развёртки (видео 5)| Объём и ПлощадьСкачать
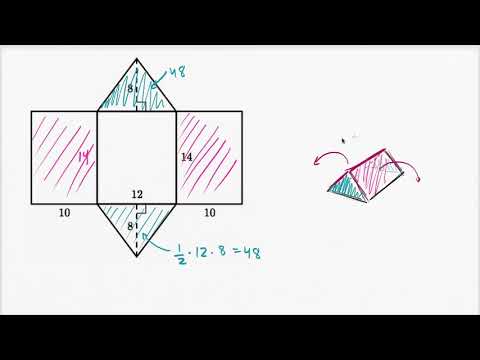
Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_$ — периметр основания;
$S_$ — площадь основания;
$S_$ — площадь боковой поверхности;
$S_$ — площадь полной поверхности;
$h$ — высота призмы.
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/$, где $h_a$ — высота, проведенная к стороне $а$
- $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√
$, где $р$ — это полупериметр $p=/$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S=/$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S=/$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S=/$, где $а$ — длина стороны.
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Цилиндр — это та же призма, в основании которой лежит круг.
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Видео:Правильная треугольная призмаСкачать

Треугольная призма все формулы и примеры задач
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Видео:Г: Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 40 боковоеСкачать

Определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Видео:№221. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 смСкачать

Элементы треугольной призмы
Треугольники ABC и A1B1C1 являются основаниями призмы .
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы .
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Видео:Найти площадь боковой поверхности правильной треугольной пирамидыСкачать

Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн . h, то получим:
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы :
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см 2 , то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм 2 , то высота должна быть выражена в мм, а объем в мм 3 и т. д.
Видео:Хитрый периметрСкачать

Пример призмы
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k 2 = S12 2 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
Формулы по математике для ЕГЭ и ОГЭ
Шар и сфера, объем шара, площадь сферы, формулы
📹 Видео
КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Задача 4.2. Объём прямой треугольной призмыСкачать
