15.
Угол MSK смежен с углом KSN, значит угол KSN равен 180° — 108° = 72°, так как сумма смежных углов равна 180°
Угол NKM равен 180° — 90° — 72° = 22°, так как сумма углов треугольника равна 180°.
Угол KNM = 90°, это видно из рисунка, он обозначен как прямой угол
16.
Числовых данных нет, поэтому буду решать в общем виде.
Угол ABC равен 30°, так как он смежен с углом 150°, а сумма смежных углов равна 180°
Угол CAB равен 60°, так как сумма углов треугольника равна 180° а два других угла равны 30° и 90°. 180° — 90° — 30° = 60°
Углы CAD и DAB равны по 30°, так как AD биссектриса, а биссектриса делит угол пополам. CD — катет, лежащий против угла в 30°, значит он равен половине гипотенузы. CD = 0,5AD
Так как углы DAB и DBA равны, то треугольник BDA — равнобедренный и AD = DB
Отсюда CB = CD+DB = 0,5AD + DB, а так как AD = DB, то CB = 0,5AD+AD=1,5AD
17.
Обратная задача задаче 16. Так как PS = 0,5 RS, то угол PRS равен 30°, значит угол PRQ = 60°, так как RS — биссектриса.
Угол RQP равен 30°(смотрите задачу 16). Значит угол RQT равно 180° — 30° = 150°
SQ = 15,6, так как треугольник RSQ — равнобедренный и RS = SQ(смотрите решение задачи номер 16)
18.
Периметр треугольника MKR равен MK + KR + MR = 32
Треугольники MRE и NRE равны по двум сторонам и углу между ними, так как RE = RE, ME = NE, угол MER равен углу NER и равен 90°
KR + MR = KR + NR = KN = 26
Подставляем в формулу периметра:
P = MK + KR + MR = MK + KR + NR = MK + KN = 32
Видео:Подготовка к ОГЭ по математике. Задача 26Скачать

Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Видео:ОГЭ по математике. Задача 26Скачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:ОГЭ Задание 26 Подобные треугольникиСкачать

Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Видео:ОГЭ задание 26Скачать

Задачки по готовым чертежам. Тема: Теорема Пифагора.Надо найти х.
Задачки по готовым чертежам. Тема: Аксиома Пифагора.
Надо отыскать х.
- Алиса Анучкин-Тимофеева
- Геометрия 2019-06-15 13:38:52 0 1
9) Набросок 1: тр. KML — равнобедренный ( КМ = МL )
Отложим отрезок МN, одинаковый отрезку KM, на её продолжении ***** угол NML = 180 — 120 = 60 ***** тр. NML — равносторонний, то есть на стороне ML построили равносторонний треугольник наружным образом ***** KM = ML = MN = NL = x
По аксиоме Пифагора в тр. KNL:
KN^2 = KL^2 + NL^2
10) тр. RTS — прямоугольный , угол Т = 90
По теореме Пифагора в тр. RTS:
RS^2 = RT^2 + TS^2
TS^2 = 13^2 — 12^2
TS^2 = 169 — 144 = 25
TS = 5
Площадь треугольника RTS:
S rts = TM RS / 2 = RT TS / 2
TM RS = RT TS
TM = RT TS / RS = 12 5 / 13 = 60 / 13 = 4_8/13
11) тр. АСВ — равнобедренный ( АС = СВ )
CD — высота, медиана, биссектриса **** AD = DB = 10/2 = 5
По теореме Пифагора в тр. BCD:
CD^2 = 13^2 — 5^2 = 169 — 25 = 144
CD = 12
Плошадь тр. АСВ:
S acb = CD AB / 2 = AE CB / 2
CD AB = AE CB
AE = CD AB / CB = 12 10 / 13 = 120 / 13 =
9_3/13
12) KMRN — ромб ( KM = MR = RN = KN )
Диагонали ромба взаимно перпендикулярны, разделяющие ромб на 4 одинаковых прямоугольных треугольника. Диагонали ромба точкой скрещения делятся напополам ***** Пусть точка О — точка скрещения диагоналей ромба ***** KO = OR = 10/2 = 5 ***** MO = ON = 12/2 = 6
По аксиоме Пифагора в тр. МОК:
МК^2 = 5^2 + 6^2 = 25 + 36 = 61
МК = V61
13) АBCD — ромб ( AB = BC = CD = AD )
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся напополам ***** Пусть точка О — точка скрещения диагоналей ромба ***** ВO = OD = 12/2 = 6
По аксиоме Пифагора в тр. ВОС:
ОС^2 = 10^2 — 6^2 = 100 — 36 = 64
ОС = 8
АС = 2ОС = 28 = 16
14)
Применим для тр. MNK теорему Пифагора:
MK^2 = MN^2 + NK^2
25^2 = 7^2 + 24^2
625 = 49 + 576
625 = 625
Как следует, по аксиоме, обратной теореме Пифагора, следует, что тр. МNK — прямоугольный ( угол N = 90 )
Площадь тр. MNK:
S mnk = NL MK / 2 = MN NK / 2
NL MK = MN NK
NL = MN NK / MK = 7 24 / 25 = 168/25 = 6,72
15) SRLK — прямоугольник
Явно, что в этой задачке не хватает данных для её решения
Допустим, что в условии задачки знаменита сторона KS = 5, тогда
По теореме Пифагора в тр. LKS:
SL^2 = KS^2 + KL^2
SL^2 = 5^2 + 12^2 = 25 + 144 = 169
SL = 13
16)
Применим для тр. МКТ аксиому Пифагора:
МТ^2 = КТ^2 + МК^2
34^2 = 30^2 + 16^2
1156 = 900 + 256
1156 = 1156
Означает, по аксиоме, оборотной аксиоме Пифагора, следует, что тр. МКТ — прямоугольный ( угол К = 90 )
Пропорциональные отрезки в прямоугольном треугольнике:
МК^2 = MN MT
16^2 = MN 34
256 = MN 34
MN = 256/34 = 128/17 = 7_9/17
🔍 Видео
ОГЭ по математике. Задача 26Скачать

Демо-вариант ОГЭ. Задача 26Скачать

Математика ОГЭ. Задача 26_4Скачать
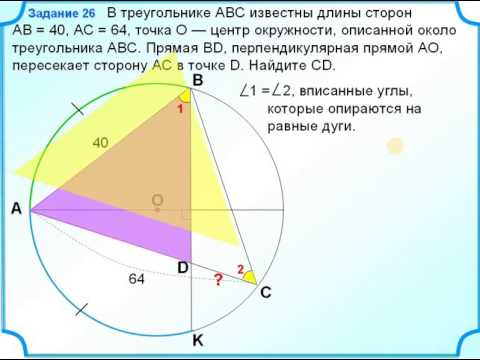
№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
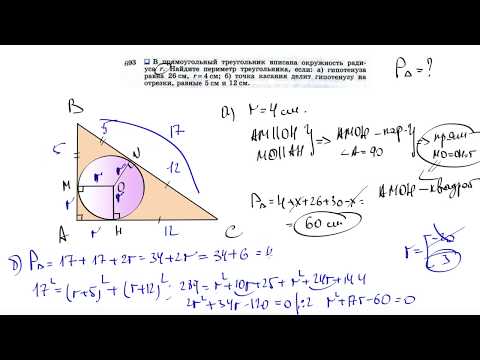
Задание 26 Отношение площадей подобных треугольниковСкачать

ОГЭ по математике, задание 26Скачать

ОГЭ Задание 26 Подобные треугольникиСкачать

ОГЭ Задание 26 Свойства площадейСкачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Площадь треугольника. Как найти площадь треугольника?Скачать

№26. Сторона АС треугольника ABC параллельна плоскости α, а стороныСкачать

ОГЭ Задание 26 Треугольник Вписанная окружность ПлощадьСкачать

Задание 26 ОГЭ по математикеСкачать

ОГЭ по математике. 9 класс. Задача 26 Вариант 3.Скачать

ОГЭ математика. Задача 26. Отношение площадей треугольников.Скачать
