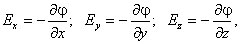Вектор градиента потенциала в точке (3 видео)

Вектор градиента потенциала в точке

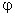
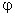
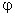
Для установления связи между силовой характеристикой электрического поля — напряжённостью и его энергетической характеристикой — потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: d A = q E d l, эта же работа равна убыли потенциальной энергии заряда q: d A = — d W _п = — q d , где d — изменение потенциала электрического поля на длине перемещения d l. Приравнивая правые части выражений, получаем: E d l = — d или в декартовой системе координат

E_x d x + E_y d y + E_z d z = — d 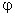, (1.8)

где E_x, E_y, E_z — проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

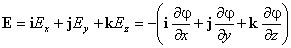
Стоящее в скобках выражение является градиентом потенциала j , т. е.

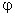
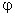
E = — grad = — Ñ .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

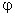
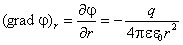
Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4 p e ₀ e r . Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора

Проекция же градиента потенциала на направление вектора t , перпендикулярного вектору r, равна

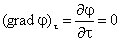
т. е. в этом направлении потенциал электрического поля является постоянной величиной ( 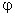= const ) .

В рассмотренном случае направление вектора r совпадает с направлением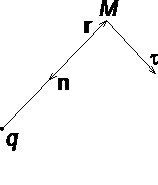
рис. 1.6

силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.

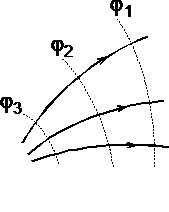
рис. 1.7

При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали — штриховыми.

Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.

1) Какова связь между напряженностью и потенциалом. Выведите ее и объясните.

2) Электростатическое поле имеет вид Е = a i + b j , где a и b константы. Является ли поле однородным. Написать выражение для потенциала поля.

3) Потенциал некоторого электростатического поля имеет вид 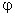= ( x 2 + y 2 + z 2 ). Что можно сказать о характере поля. Найти модуль напряженности поля в точке с координатами x , y , z

4) Чему равна работа по перемещению заряда вдоль эквипотенциальной поверхности

Видео:Градиент в точке.Скачать

Вектор градиента потенциала в точке

§7 Работа силы электростатического поля при перемещении заряда.

Потенциальный характер сил поля.

Циркуляция вектора напряженности

Рассмотрим электростатическое поле, создаваемое зарядом q . Пусть в нем перемещается пробный заряд q ₀ . В любой точке поля на заряд q ₀ действует сила

де — модуль силы, — орт радиус-вектора , определяющего положение заряда q ₀ относительно заряда q . Так как сила меняется от точки к точке, то работу силы электростатического поля запишем как работу переменной силы:

Ввиду того, что рассматривали перемещение заряда из точки 1 в точку 2 по произвольной траектории, можно сделать вывод, что работа по перемещению точечного заряда в электростатическом поле не зависит от формы пути, а определяется лишь начальным и конечным положением заряда. Это свидетельствует о том, что электростатическое поле является потенциальным, а сила Кулона – консервативной силой. Работа по перемещению заряда в таком поле по замкнутому пути всегда рвана нулю.

— проекция на направление контура ?.

Учтем, что работа по замкнутому пути равно нулю

— ЦИРКУЛЯЦИЯ вектора напряженности.

Циркуляция вектора напряженности электростатического поля, взятая по произвольному замкнутому контуру всегда равна нулю.

§7 Потенциал.

Связь между напряженностью и потенциалом.

Градиент потенциала.

Эквипотенциальные поверхности

Поскольку электростатическое поле является потенциальным работа по перемещению заряда в таком поле может быть представлена, как разность потенциальных энергий заряда в начальной и конечной точках пути. (Работа равна уменьшению потенциальной энергии, или изменению потенциальной энергии, взятому со знаком минус.)

Постоянную определяют из условия, что при удалении заряда q ₀ на бесконечность его потенциальная энергия должна быть равна нулю.

Различные пробные заряды q ₀ _i , помещенные в данную точку поля будут обладать в этой точке различными потенциальными энергиями:

…

Отношение W _пот _i к величине пробного заряда q ₀ _i , помещенного в данную точку поля является величиной постоянной для данной точки поля для всех пробных зарядов. Это отношение называется ПОТЕНЦИАЛОМ.

ПОТЕНЦИАЛ – энергетическая характеристика электрического поля. ПОТЕНЦИАЛ численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Работу по перемещению заряда можно представить в виде

Потенциал измеряется в Вольтах

ЭКВИПОТЕНЦИАЛЬНЫМИ ПОВЕРХНОСТЯМИ называются поверхности равного потенциала (φ = const ). Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Связь между напряженностью и потенциалом φ можно найти, исходя из того, что работу по перемещению заряда q на элементарном отрезке d ? можно представить как

С другой стороны

— градиент потенциала.

Напряженность поля равна градиенту потенциала, взятому со знаком минус.

Градиент потенциала показывает, как меняется потенциал на единицу длины. Градиент перпендикулярен функции и направлен в сторону возрастания функции. Следовательно, вектор напряженности перпендикулярен эквипотенциальной поверхности и направлен в сторону убывания потенциала.

Рассмотрим поле, создаваемое системой N точечных зарядов q ₁ , q ₂ , … q_N . Расстояния от зарядов до данной точки поля равны r ₁ , r ₂ , … r_N . Работа, совершаемая силами этого поля над зарядом q ₀ , будет равна алгебраической сумме работ сил, каждого заряда в отдельности.

гле

Потенциал поля, создаваемого системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в этой же точке каждым зарядом в отдельности.

§9 Вычисление разности потенциалов плоскости, двух плоскостей, сферы, шара, цилиндра

Используя связь между φ и определим разность потенциалов между двумя произвольными точками

Разность потенциалов поля равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ.

2. Разность потенциалов поля двух бесконечных параллельных разноименно заряженных плоскостей с поверхностной плотностью заряда σ.

Если х₁ = 0; х₂ = d , то или

3. Разность потенциалов поля равномерно заряженной сферической поверхности радиуса R .

Внутри сферической поверхности потенциал всюду одинаков и равен

4. Разность потенциалов поля объемно заряженного шара радиуса R с общим зарядом Q.

Вне шара r ₁ , r ₂ > R ,

Внутри шара

5. Разность потенциалов поля равномерно заряженного цилиндра (или бесконечно длинной нити).

r > R :

Видео:ГрадиентСкачать

Связь меяеду напряженностью и потенциалом электростатического поля

Силовая характеристика электростатического поля — напряженность Е и энергетическая характеристика — потенциал . Модуль этого вектора равен изменению потенциала со знаком «минус». Знак «минус» говорит о том, что вектор напряженности Е электростатического поля направлен в сторону убывания потенциала q>.

Рассмотрим связь между напряжённостью Е и потенциалом , не вдоль линии напряжённости Е, то вводят координатные оси о х, о у, о z и определяют проекции вектора напряженности Е на оси о х, о у, о z