Как построить чертеж параллелепипеда по векторам (2 видео)

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Содержание

Правило параллелепипеда
Разложение вектора по двум неколлинеарным векторам
Сумма нескольких векторов
Правило многоугольника или правило цепи
Свойство сочетательности
Правило параллелепипеда
Ориентированные площади и объёмы
Ориентированная площадь параллелограмма
Ориентированный объем параллелепипеда
📺 Видео

Видео:Правило параллелепипеда для векторовСкачать

Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

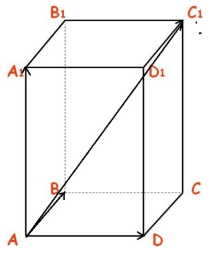
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow $ и $overrightarrow $ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

Доказательство.

Существование: Пусть нам даны три некомпланарных вектора $overrightarrow , overrightarrow $ и $overrightarrow $. Выберем произвольную точку $O$ и построим следующие векторы:

[overrightarrow =overrightarrow, overrightarrow =overrightarrow, overrightarrow =overrightarrow и overrightarrow

=overrightarrow]

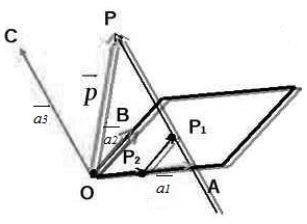
Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:

Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow$ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

$ по векторам $overrightarrow , overrightarrow $ и $overrightarrow $:

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

Видео:§20 Нахождение объёма параллелипипеда Скачать

Сумма нескольких векторов

Сумма нескольких векторов а ₁, а ₂, а ₃, … , а _n, это вектор, получающийся после ряда последовательных сложений: к вектору а ₁ прибавляется вектор а ₂, к полученному вектору прибавляется вектор а ₃ и т.д.

Из определения вытекает такое построение

Видео:Площадь параллелограмма, построенного на данных векторахСкачать

Правило многоугольника или правило цепи

Из произвольного начала О строим вектор ОА ₁ = а ₁, из точки А ₁, как из начала, строим вектор А ₁ А ₂ = а ₂, из точки А ₂ строим вектор А ₂ А ₃ = а ₃ и т.д. Вектор ОА _n (на рисунке n = 6) есть сумма векторов а ₁, а ₂, … , а _n.

Видео:Площадь параллелограмма по векторамСкачать

Свойство сочетательности

Слагаемые векторы можно группировать как угодно.

Так, если найти сначала сумму векторов

и к ней прибавить вектор а ₁ ( ОА ₁), то получим то же вектор:

Видео:№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

Правило параллелепипеда

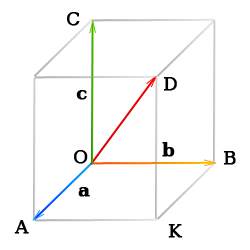
Если три вектора а , b , с после приведения к общему началу не лежат в одной плоскости, то сумму а + b + c можно найти таким построением:

Из любого начала О строим векторы ОА = а , ОВ = b , ОС = с , на отрезках ОА , ОВ , ОС , как на ребрах, строим параллелепипед. Вектор диагонали OD есть сумма векторов a , b , и c (так как ОА = а , АК = ОВ = b , KD = OC = c и OD = OA + AK + KD ).

К векторам, которые (после приведения к общему началу) лежат в одной плоскости, это построение неприменимо.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Ориентированные площади и объёмы

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Ориентированная площадь параллелограмма

Ориентированной площадью параллелограмма , построенного на неколлинеарных векторах и , называется его площадь , взятая со знаком плюс, если ориентация пары векторов и правая , и со знаком минус, если ориентация — левая

Внешним (косым) произведением неколлинеарных векторов и на плоскости называется число, равное ориентированной площади параллелограмма, построенного на этих векторах. Если векторы и коллинеарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается . Его свойства повторяют алгебраические свойства векторного произведения, т.е. для любых векторов на плоскости и любого числа справедливы равенства:

4) Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то внешнее произведение этих векторов находится по формуле

Если — координатные столбцы векторов в стандартном базисе на плоскости, то их внешнее произведение находится по формуле

Приведенные свойства внешнего произведения следуют из алгебраических свойств векторного произведения, если векторы на плоскости рассматривать как векторы в пространстве с нулевыми аппликатами.

Рассмотрим задачу разложения вектора по базису на плоскости. Отложим все векторы от произвольной точки . Сначала разберем случаи, когда векторы и коллинеарны: одинаково направлены (рис.1.49,а) или противоположно направлены (рис. 1.49,6). В этих случаях ордината вектора равна нулю, а абсцисса находится как отношение

так как пара в первом случае правая (рис.1.49,а), а во втором случае — левая (рис.1.49,б).

Пусть теперь векторы и не коллинеарны (рис.1.49,в). Построим проекции и на прямые, содержащие базисные векторы: . Из концов векторов и опустим перпендикуляры и соответственно на прямую, содержащую вектор . Учитывая, что векторы и противоположно направлены, а также подобие прямоугольных треугольников с гипотенузами и , находим абсциссу вектора :

так как пара — правая, а пара — левая. Аналогично находится ордината (векторы и одинаково направлены)

Таким образом, вектор имеет следующее разложение по базису на плоскости:

Рассмотрим применение формулы (1.19) для решения системы двух линейных уравнений с двумя неизвестными:

Эту систему можно записать в виде .Рассматривая полученные столбцы как координатные столбцы векторов в стандартном базисе на плоскости, получаем разложение .

Таким образом, нахождение решения системы уравнений свелось к задаче разложения вектора по векторам и . Предполагая, что коэффициенты при неизвестных не пропорциональны, т.е. (векторы и не коллинеарны), по формуле (1.19), полагая , получаем:

Видео:Как строить сечения параллелепипедаСкачать

Ориентированный объем параллелепипеда

Ориентированным объемом параллелепипеда , построенного на некомпланарных векторах , называется его объем , взятый со знаком плюс, если ориентация тройки векторов правая и со знаком минус, если ориентация — левая .

Внешним (косым) произведением некомпланарных векторов называется число, равное ориентированному объему параллелепипеда, построенного на этих векторах. Если векторы компланарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается .

Внешнее произведение трех векторов совпадает с их смешанным произведением (в силу первого геометрического свойства смешанного произведения), т.е. . В ортонормированием базисе

так как определитель транспонированной матрицы равен определителю исходной матрицы.

При помощи ориентированных объемов задача разложения вектора по базису в пространстве решается так же как и на плоскости с использованием ориентированных площадей. В результате получаем

Формула (1.21) соответствует правилу Крамера решения системы трех линейных уравнений с тремя неизвестными.

Пример 1.23. Заданы координатные столбцы

векторов в стандартном базисе. Разложить вектор по векторам .

Решение. По формуле (1.20) находим смешанные произведения

Коэффициенты разложения определяем по формуле (1.21):