Вектор электрического смещения и магнитная индукция (5 видео)

Вектор электрической индукции

Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

D → = ε 0 E → + P → , где ε 0 — электрическая постоянная, E → — вектор напряженности, P → — вектор поляризации.

Вектор электрического смещения в СНС определяется как:

Содержание

Вектор индукции
Связь вектора напряженности и вектора электрического смещения
ЭЛЕМЕНТЫ ТЕОРИИ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Вихревое электрическое поле
Ток смещения. Обобщенная теорема о циркуляции вектора Н
Вектор электрической индукции
Определение вектора электрической индукции
Физический смысл вектора электрической индукции
Теорема Гаусса — Остроградского для поля в диэлектрике
Примеры задач с решением
🔍 Видео

Видео:Лекция 237. Вектор электрической индукцииСкачать

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

По уравнению d i v D → = ρ видно, что для D → единственным источником будут являться свободные заряды, на которых данный вектор начинается и заканчивается. В точках с отсутствующими свободными зарядами вектор электрической индукции является непрерывным. Изменения напряженности поля, вызванные наличием связанных зарядов, учитываются в самом векторе D → .

Видео:Электромагнитная индукция. Простыми словамиСкачать

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

D → = ε 0 E → + ε 0 χ E → = ε 0 + ε 0 χ E → = ε ε 0 E → .

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

D 2 n — D 1 n = σ

n 2 → D 2 → — D 1 → = σ ,

где σ – поверхностная плотность распределения зарядов на границе диэлектриков, n 2 → — нормаль, проведенная в сторону второй среды.

Формула тангенциальной составляющей:

D 2 τ = ε 2 ε 1 D 1 τ .

Единица вектора электрической индукции измеряется в системе С И как К л м 2 .

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Имеются пластины плоского конденсатора с зарядом q . Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью ε ≠ ε υ o z d .

Поле конденсатора в первом случае характеризовалось вектором смещения ε v o z d = 1 , то есть D 1 → = ε v o z d ε 0 E 1 → = ε 0 E 1 → .

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ .

Формула плотности связанных зарядов:

Произведем подстановку σ s υ = χ ε 0 E в E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ , тогда:

Далее выражаем из ( 1 . 6 ) напряженность поля Е . Формула принимает вид:

E = E 1 1 + χ = E 1 ε .

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

D = ε ε 0 E 1 ε = ε 0 E 1 = D 1 .

Ответ: вектор электрической индукции не изменяется.

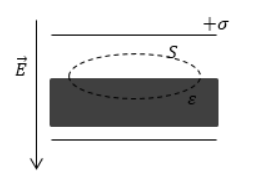
Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Φ D = ∫ S D → · d S → .

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

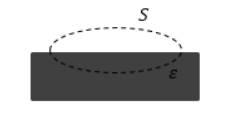
Изображена замкнутая поверхность S , проходящая с захватом части пластины изотропного диэлектрика на рисунке 2 . Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности > 0 . Какой вывод можно сделать из данной задачи?

Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Φ D = ∫ S D → · d S → = Q = 0 .

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.

Видео:45. Электрическое смещениеСкачать

ЭЛЕМЕНТЫ ТЕОРИИ МАКСВЕЛЛА ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Видео:1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

Вихревое электрическое поле

Для объяснения ЭДС индукции в неподвижных проводниках (см. § 70) Максвелл предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. Согласно представлениям Максвелла, контур, в котором появляется ЭДС, играет второстепенную роль, являясь своего рода лишь «прибором», обнаруживающим это поле.

Таким образом, согласно Максвеллу, изменяющееся во времени магнитное поле порождает электрическое поле Е_в, циркуляция которого [см. (70.3)1,

по неподвижному контуру L представляет собой ЭДС электромагнитной индукции. В формуле

(77.1) Е_В1 — проекция вектора Е_в на направление d/.

Учитывая, что Ф = J BdS |см. (60.2)), выра-

жение (77.1) можно записать в виде

Если поверхность и контур неподвижны, то операции дифференцирования и интегрирования можно поменять местами. Следовательно,

где символ частной производной подчеркивает тот

факт, что интеграл J Z?d5 является функцией толь-

Циркуляция вектора напряженности электростатического поля (обозначим его E_Q) вдоль любого замкнутого контура, согласно (7.3), равна нулю:

Из выражений (77.2) и (77.3) следует, что рассматриваемые поля (Ё„ и t_Q) различаются принципиально: циркуляция вектора Ё_н в отличие от циркуляции вектора E_Q не равна нулю.

Следовательно, электрическое поле Е_д, возбуждаемое магнитным полем, как и само магнитное поле (см. § 58), является вихревым.

Видео:Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Ток смещения. Обобщенная теорема о циркуляции вектора Н

Максвелл высказал гипотезу, что если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое иоле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля.

Для установления количественных связей между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.

Согласно теореме Гаусса (20.3) для электростатического поля в диэлектрике, поток вектора электрического смещения сквозь произвольную замкнутую поверхность 5

где Q — алгебраическая сумма свободных электрических зарядов, охватываемых этой поверхностью.

Продифференцируем выражение (78.1) по времени:

где операции дифференцирования и интегрирования поменяли местами (поверхность неподвижна и не деформируется), а символ частной производной подчеркивает тот факт, что интеграл ф DdS

является только функцией времени.

Оказалось, что правая часть выражения (78.3) имеет размерность силы тока. Кроме того, сравнивая выражения (78.3) и / = JydS [см. (30.5)],

видим, что — имеет размерность плотности тока.

Эту величину Максвелл назвал плотностью тока смещения.

Током смещения сквозь произвольную поверхность S называют

т. е. ток смещения определяется потоком вектора плотности тока смещения сквозь поверхность S.

Рассмотрим направление векторов j и j_cu. При зарядке конденсатора (рис. 105, а) через проводник, соединяющий обкладки, ток течет от верхней обкладки к нижней. В данном случае поле в

конденсаторе усиливается — > 0 , вектор j = —

направлен в ту же сторону, что и D, т. е. направления у и у_см совпадают.

В случае разрядки конденсатора (рис. 105, б) через проводник, соединяющий обкладки, ток течет от нижней обкладки к верхней. Поле в конден-

саторе ослабляется — д ‘ ) д1

направлен противоположно вектору D. Однако

вектор — опять-таки направлен как и вектор j .

Из рассмотренных примеров следует, что направление вектора у, а следовательно, и вектора

у_см совпадает с направлением вектора —, как

это и следует из формулы (78.4).

Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 105 штриховыми линиями).

В диэлектрике вектор электрического смещения |см. (19.2)]

где Ё — напряженность электростатического

поля, а Р — поляризованность (см. § 18). Тогда по (78.4) плотность тока смещения

где е₀ — — плотность тока смещения в вакууме;

нием зарядов, а обусловленная только изменением электрического поля во времени, также возбуждает магнитное поле, является принципиально новым утверждением Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возникновению в окружающем пространстве магнитного поля.

Максвелл ввел понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока

Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рассмотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Максвелл обобщил теорему о циркуляции, добавив в правую часть уравнения (64.9) ток смещения (78.4) сквозь поверхность S, натянутую на замкнутый контур L:

Выражение (78.8) — обобщенная теорема о циркуляции вектора Н: циркуляция вектора напряженности Н магнитного поля по произвольному неподвижному замкнутому контуру равна алгебраической сумме токов проводимости и тока смещения, охватываемых этим контуром.

Выражение (78.8) справедливо всегда, свидетельством чего является полное соответствие теории и опыта. Экспериментальным подтверждением этого уравнения являются опыты А.А. Эйхенвальда, изучившего магнитное поле тока поляризации, который, как следует из (78.6), является частью тока смещения.

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор электрической индукции

Допустим, что одно вещество имеет диэлектрическую проницаемость равную $_1$, а вторая $_2$, тогда нормальная составляющая вектора напряженности электростатического поля ($E_n$) уменьшается во столько раз, во сколько увеличивается диэлектрическая проницаемость среды:

где $E_$ — нормальная компонента напряженности поля в веществе 1; $E_$ — нормальная составляющая электростатического поля во втором веществе. Отметим, что при переходе из одного вещества в другое тангенциальная компонента вектора напряженности ($E_$) изменяется без скачка. Говорят, что на границе двух веществ происходит «преломление» силовых линий поля.

Для сохранения всех преимуществ, которые дает теорема Остроградского — Гаусса при рассмотрении электростатического поля в вакууме, в веществе вводят физическую величину, которая не испытывает скачка при переходе из одного вещества в другое с разными $varepsilon $.

Так как при переходе из вакуума в вещество с диэлектрической проницаемостью равной $varepsilon $ число силовых линий уменьшается в $varepsilon $ раз, то векторная величина, равная:

будет оставаться неизменной при переходе из одного вещества в другое.

Видео:Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать

Определение вектора электрической индукции

Векторная величина, обозначаемая $overline$, равная:

где $overline

$ — вектор поляризации.

Выражение (3) является наиболее общим определение вектора электрической индукции (вектора электрического смещения). Для большинства диэлектриков (исключением являются, например, сегнетоэлектрики) вектор поляризации пропорционален напряженности поля:

В таком случае от формулы (3) мы приходим к определению вектора электрической индукции вида (2).

Название «вектор индукции» указывает на связь вектора $overline$ и явления электризации по влиянию (явление электростатической индукции).

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Физический смысл вектора электрической индукции

Допустим, что в веществе, с диэлектрической проницаемостью равной $varepsilon $ имеется очень тонкий вакуумный зазор, грани которого перпендикулярны направлению поля в точке рассмотрения (рис.1). В эту щель помещают точечный единичный положительный пробный заряд. Сила, с которой поле будет оказывать действие на этот пробный заряд, равна $overline.$

И так, вектор электрической индукции — это сила, которая действует на точечный единичный положительный заряд, находящийся в бесконечно узком зазоре, грани которого перпендикулярны направлению поля.

Силовые линии вектора $overline$ начинаются и заканчиваются на свободных зарядах. Величина $overline$ не зависит от диэлектрической проницаемости вещества.

В некоторых источниках вектор электрической индукции называют формальным, так как он равен сумме физических величин, относящихся к разным объектам к полю и к веществу (см формулу (3), где $overline$ — характеристика электрического поля; $overline

$ — характеристика вещества). Тогда говорят, что вектор электрической индукции не имеет физического смысла.

Видео:Лекция №4 "Диэлектрики, вектор электрической индукции"Скачать

Теорема Гаусса — Остроградского для поля в диэлектрике

Поток вектора электрической индукции равен алгебраической сумме свободных зарядов, которые находятся внутри рассматриваемой замкнутой поверхности:

По теореме (5) поток вектора $overline$ через любую замкнутую поверхность равен нулю, если внутри данной поверхности нет свободных зарядов. Заряды, находящиеся вне рассматриваемой поверхности на поток вектора $overline$, не влияют.

Видео:Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать

Примеры задач с решением

Задание. Чему равен вектор поляризации в некоторой точке однородного изотропного диэлектрика, если известен вектор электрической индукции в этой точке ($overline$)? Диэлектрическая проницаемость вещества равна $varepsilon $.

Решение. За основу решения задачи примем определение вектора электрического смещения вида:

Выразим вектор поляризации из (1.1):

Так как по условию рассматриваемый диэлектрик является однородным и изотропным, то:

[overline=varepsilon _0overline left(1.3right),]

Подставим правую часть формулы (1.4) вместо $overline$ в уравнение (1.2), имеем:

Ответ. $overline

=left(1-fracright)overline$

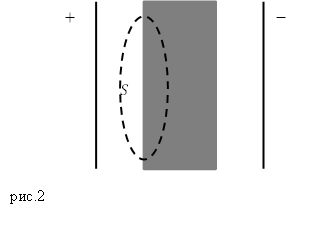
Задание. Между двумя бесконечными заряженными пластинами, несущими одинаковые по величине, но противоположные по модулю заряды поместили пластину из диэлектрика. Пластина сторонних зарядов не имеет. Каков поток вектора электрической индукции через поверхность, которая изображена на рис.2?

Решение. В соответствии с теоремой Гаусса поток вектора электрической индукции равен алгебраической сумме свободных зарядов, которые находятся внутри выделенной замкнутой поверхности (рис.2). Так как по условию задачи свободных зарядов между пластинами и в диэлектрике нет, то поток вектора $overline$ будет равен нулю:

Ответ. $ointnolimits_S<overlinedoverline~~=0 >$~~