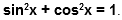Ординатой точки единой окружности называется

sin α = y —
ордината точки P_α
cos α = x —
абсцисса точки P_α

1. Определение тригонометрических функций
Через единичную окружность (R = 1)	Через произвольную окружность (R — радиус окружности)	Через прямоугольный треугольник (для острых углов)

tg α = y/x = sin α / cos α

ctg α = x/y = cos α / sin α

2. Тригонометрические функции числового аргумента

sin (числа α) = sin (угла в α радиан)

cos (числа α) = cos (угла в α радиан)

tg (числа α) = tg (угла в α радиан)

ctg (числа α) = ctg (угла в α радиан)

3. Линии тангенсов и котангенсов

tg α = y_A —
ордината соответствующей точки линии тангенсов

СВ — линия котангенсов (СВ || Oх)
ctg α = x_B —
абсцисса соответствующей точки линии котангенсов

Объяснение и обоснование

1. Определение тригонометрических функций. Из курса геометрии вам известно определение тригонометрических функций острого угла в прямоугольном треугольнике. Напомним их.

Синусом острого угла α в прямоугольном треугольнике называется отношение длины противолежащего катета к длине гипотенузы: sin α = a / c (рис. 61).

Косинусом острого угла α в прямоугольном треугольнике называется отношение длины прилежащего катета к длине гипотенузы: cos α = b / c.

Тангенсом острого угла α в прямоугольном треугольнике называется отношение длины противолежащего катета к длине прилежащего: tg α = a / b.

Котангенсом острого угла α в прямоугольном треугольнике называется отношение длины прилежащего катета к длине противолежащего: ctg α = b / a.

В курсе геометрии было обосновано, что синус и косинус острого угла зависят только от величины угла и не зависят от длин сторон треугольника и его расположения, то есть синус и косинус (а таким образом, и тангенс, и котангенс) являются функциями величины угла, которые называются тригонометрическими функциями.

Для сокращения формулировок мы будем использовать термин «тригонометрическая функция угла», понимая, что рассматривается «тригонометрическая функция величины угла» (при этом величина угла может быть выражена как в радианах, так и в градусах).

Также в курсе геометрии с использованием окружности с центром в начале координат было введено определение тригонометрических функций для углов от 0° до 180°. Эти определения можно применить для нахождения тригонометрических функций любых углов. Напомним их (но теперь будем рассматривать любые углы α от –∞ до +∞).

Возьмем окружность радиуса R с центром в начале координат. Обозначим точку окружности на положительной полуоси абсцисс через P₀ (рис. 62). Необходимые нам углы будем образовывать поворотом радиуса OP₀ около точки O. Пусть в результате поворота на угол α около точки O радиус OP₀ займет положение OP_α (говорят, что при повороте на угол α радиус OP₀ переходит в радиус OP_α, а точка P₀ переходит в точку P_α). Напомним, что при α > 0 радиус OP₀ поворачивается против часовой стрелки, а при α * . Удобно взять R = 1, что позволит несколько упростить приведенные определения тригонометрических функций.

* Это следует из того, что две концентрические окружности гомотетичны (центр гомотетии — точка О, а коэффициент гомотетии k — отношение радиусов этих окружностей), тогда и точки Pα на этих окружностях также будут гомотетичны. Таким образом, при переходе от одной окружности к другой в определениях тригонометрических функций числитель и знаменатель соответствующей дроби умножаются на k, а значение дроби не изменяется.

Окружность радиуса 1 с центром в начале координат будем называть единичной окружностью.

Пусть при повороте на угол α точка P₀ (1; 0) переходит в точку P_α (x; y)
(то есть при повороте на угол α радиус OP₀ переходит в радиус OP_α) (рис. 63).

Синусом угла α называется ордината точки P_α (x; y) единичной окружности:

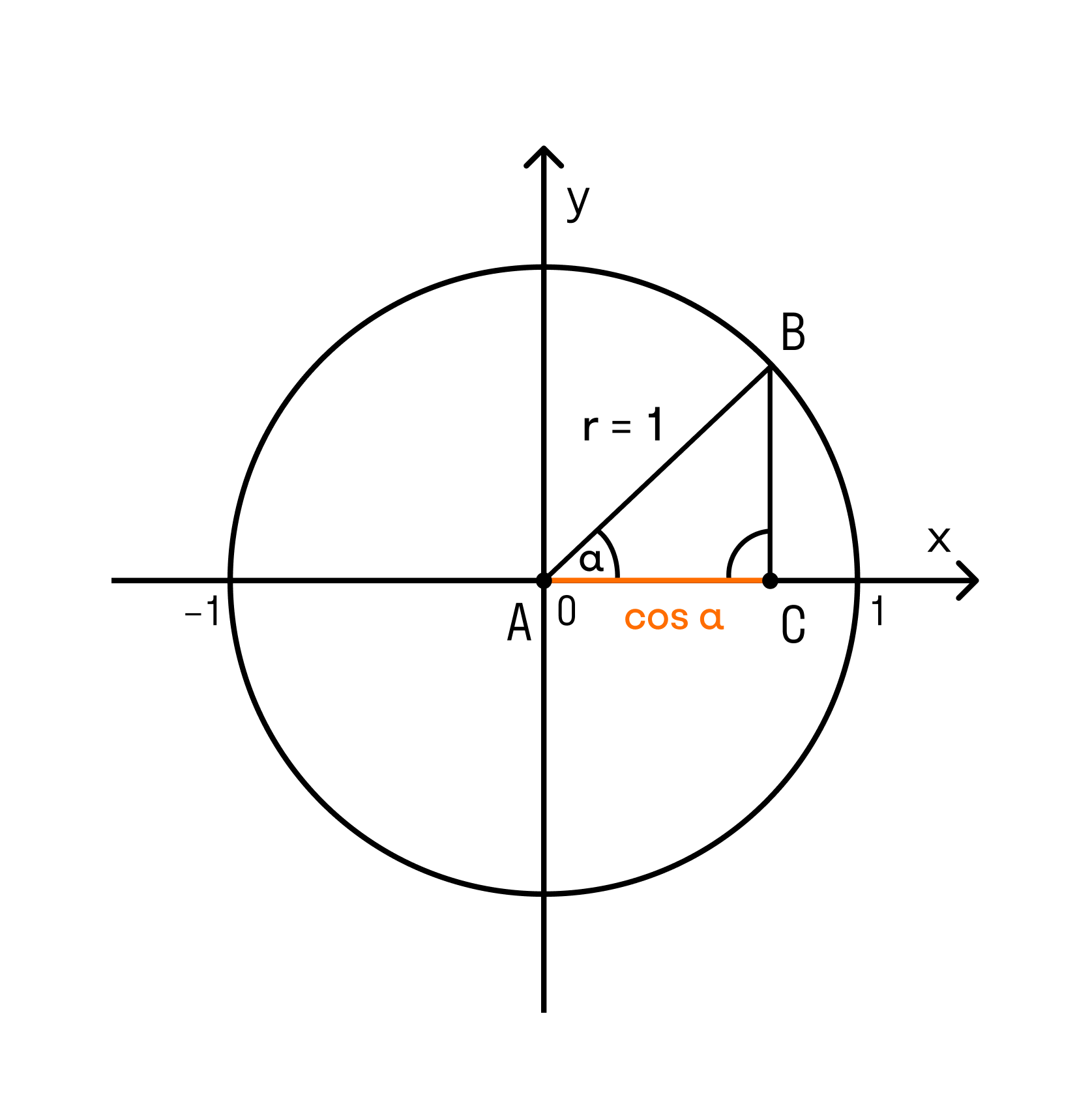
Косинусом угла α называется абсцисса точки P_α (x; y) единичной окружности:

Тангенсом угла α называется отношение ординаты точки P_α (x; y) единичной окружности к ее абсциссе, то есть отношение sin α / cos α.

Таким образом, tg α = sin α / cos α (где cos α ≠ 0).

Заметим, что при cos α = 0 значение функции tg α не определено, а значение функции ctg α не определено при sin α = 0.

Пример

Пользуясь этими определениями, найдем синус, косинус, тангенс и котангенс угла 2π / 3 радиан.

♦ Рассмотрим единичную окружность (рис. 64). При повороте на угол 2π / 3 радиус OP₀ переходит в радиус OP_2π/3 (а точка P₀ переходит в точку P_2π/3). Координаты точки P_2π/3 можно найти, используя свойства прямоугольного треугольника OAP_2π/3 (с углами 60° и 30° и гипотенузой 1): x = — OA=−1/2; y = AP_2π/3 = √3/2. Тогда: sin 2π/3 = y = √3/2; cos 2π/3 = x = -1/2; tg 2π/3 = sin 2π/3 / cos 2π/3 = — √3; ctg 2π/3 = — 1/√3.◊

Аналогично находятся значения синуса, косинуса, тангенса и котангенса углов, градусные и радианные меры которых указаны в верхней строке таблицы 19 (с. 156).

Укажем, что таким образом можно найти тригонометрические функции только некоторых углов. Тригонометрические функции произвольного угла обычно находят с помощью калькулятора или таблиц.

2. Тригонометрические функции числового аргумента. Введенные определения позволяют рассматривать не только тригонометрические функции углов, но и тригонометрические функции числовых аргументов, если рассматривать тригонометрические функции числа α как соответствующие тригонометрические функции угла в α радиан. То есть:

синус числа α — это синус угла в α радиан;
косинус числа α — это косинус угла в α радиан.

Например: sin π/6 = sin (π/6 радиан) = sin 30° = 1/2 (см. также пункт 2 табл. 7).

α	градусы	0 º	30 º	45 º	60 º	90 º	180 º	270 º	360 º
	радианы	0	π/6	π/4	π/3	π/2	π	3π/2	2π
sin α		0	1/2	√2/2	√3/2	1	0	-1	0
cos α		1	√3/2	√2/2	1/2	0	-1	0	1
tg α		0	√3/3	1	√3	—	0	—	0
ctg α		—	√3	1	√3/3	0	—	0	—

3. Линии тангенсов и котангенсов. Для решения некоторых задач полезно иметь представление о линиях тангенсов и котангенсов.

♦ Проведем через точку P₀ единичной окружности прямую AP₀, параллельную оси Oy (рис. 65). Эта прямая называется линией тангенсов.
Пусть α — произвольное число (или угол), для которого cos α ≠ 0. Тогда точка P_α не лежит на оси Oy и прямая OP_α пересекает линию тангенсов в точке A. Поскольку прямая OP_α проходит через начало координат, то ее уравнение имеет вид y = kx. Но эта прямая проходит через точку P_α с координатами (cos α; sin α), значит, координаты точки P_α удовлетворяют уравнению прямой y = kx, то есть sin α = k cos α. Отсюда k = sin α / cos α = tg α. Следовательно, прямая OP_α имеет уравнение

y = (tg α) x. Прямая AP₀ имеет уравнение x = 1. Чтобы найти ординату точки A, достаточно в уравнение прямой OP_α подставить x = 1. Получаем y_A = tg α. Таким образом,

тангенс угла (числа) α — это ордината соответствующей точки на линии тангенсов.◊

Аналогично вводится и понятие линии котангенсов: это прямая CB (рис. 66), которая проходит через точку C (0; 1) единичной окружности параллельно оси Ox.

Если α — произвольное число (или угол), для которого sin α ≠ 0 (то есть точка P_α не лежит на оси Ox), то прямая OP_α пересекает линию котангенсов в некоторой точке B (x_B; 1).

Аналогично вышеизложенному обосновывается, что x_B = ctg α, таким образом,

котангенс угла (числа) α — это абсцисса соответствующей точки на линии котангенсов.

Вопросы для контроля

1. Сформулируйте определения тригонометрических функций острого угла в прямоугольном треугольнике.

2. Сформулируйте определения тригонометрических функций произвольного угла:
а) используя окружность радиуса R с центром в начале координат;
б) используя единичную окружность.

3. Что имеют в виду, когда говорят о синусе, косинусе, тангенсе и котангенсе числа α?

Упражнения

1°. Постройте на единичной окружности точку Pα, в которую переходит точка P₀ (1; 0) единичной окружности при повороте на угол α. В какой координатной четверти находится точка P_α в заданиях 3–6?
1) α = 3π; 2) α = –4π; 3) α=7π/6;

4) α=−3π/4; 5) α=4π/3; 6) α=7π/4.

2. Найдите значение sin α, cos α, tg α, ctg α (если они существуют) при:
1) α = 3π; 2) α = –4π; 3) α=−π/2;

4) α=5π/2; 5*) α=−5π/6; 6*) α=3π/4.

3°. Пользуясь определением синуса и косинуса, с помощью единичной окружности укажите знаки sin α и cos α, если:
1) α=6π/5; 2) α=−π/6; 3) α=5π/6;

4*. Пользуясь линией тангенсов, укажите знак tg α, если:
1) α=4π/3; 2) α=−3π/4; 3) α=11π/6;

5*. Пользуясь линией котангенсов, укажите знак сtg α, если:
1) α=−4π/3; 2) α=3π/4; 3) α=−11π/6;

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Тест по теме «Основы тригонометрии»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Раздел «Основы тригонометрии».

Тест разработан для учащихся 10-11 классов, а также студентов 1 курса СПО, обучающихся на базе 9 классов.

Косинусом называется … точки единичной окружности.

Тангенс угла определяется отношением

нет правильного ответа

Если угол содержит градусов, то его радианная мера равна

При каких значениях угла (в градусной мере) не существует тангенс?

Установите соответствие между видами тригонометрических уравнений.

Тригонометрическое уравнение, приводимое к квадратному

Однородное тригонометрическое уравнение

Простейшее тригонометрическое уравнение

Тригонометрическое уравнение, решаемое с помощью формул преобразования суммы одноименных тригонометрических функций в произведении

Если существует такое число Т (называемое периодом), что для всех х выполняется равенство и , то функция называется …

Укажите функцию с периодом :

На единичной окружности тангенс – это

отношение абсциссы к ординате

отношение ординаты к абсциссе

у становите соответствие:

основное тригонометрическое тождество

формула половинного аргумента

формула сложения аргументов

формула двойного аргумента

Сжатие функции произойдет, если

Установите соответствие между тригонометрическим уравнением и его решением

При , какое из уравнений не будет иметь решения?

Область определения функции

Ординатой точки единичной окружности называется:

Абсциссой точки единичной окружности называется:

Основное тригонометрическое тождество имеет вид:

sin 2 х — cos 2 х = 1

sin х + cos x = 0

sin 2 x + cos 2 х = 1

sin x + cos x — 1

Какая из функций является четной:

Укажите не верное утверждение

a .

b .

c .

d .

Продолжить выражение .

нет ни одного верного

Множество значений функций у = sin x, у = cos x является отрезок:

Арккосинусом числа а называется такое число из отрезка . косинус которого равен а

Период функций у = cos x, у = sin x равен

cos 2 a — sin 2 a

Установите соответствие между радианной и градусной мерой

При построении графика функции у = sin2x произойдет

растяжение по оси ОУ

сжатие по оси ОУ

сжатие по оси ОХ

растяжение по оси ОХ

Какие из функций являются нечетными

у = tg х, у = ctg x, у = cos х

у = tg x, у = sin x, у = cos х

у = tg х, у = ctg х, y = sin x

у = c tg x , у = sin x, у = cos х

Арктангенсом числа a называется такое число из интервала …, тангенс которого равен α.

Арккотангенсом числа а называется такое число из интервала …, котангенс которого равен α.

Синус двойного аргумента определяется формулой

в радианной мере угол в 120 0

Выразите в градусах

При построение графика функции у = 2sin x произойдет:

растяжение функции у = sin x вдоль оси ОХ

сужение функции у = sin x вдоль оси ОХ

растяжение функции у = sin x вдоль оси 0Y

сужение функции у = sin x вдоль оси 0Y

Найдите число arctg 0

Существует ли arсctg 0

Продолжить выражение cos  cos  + sin  sin 

Упростите

a.

b.

c.

d.

Укажите выражения, имеющие знак плюс

cos 250 0 ·sin 330 0

tg 175 0 ·ctg 200 0

cos 100 0 ·sin 100 0

cos 150 0 ·sin 150 0

Преобразуйте

Какая функция на отрезке является возрастающей

Шарапова Юлия Владимировна,

ОАОУ СПО «Астраханский социально педагогический колледж»,

414040 г. Астрахань, ул. Коммунистическая , 48

Дистанционные курсы для педагогов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 934 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 323 человека из 72 регионов

Ищем педагогов в команду «Инфоурок»

• Шарапова Юлия ВладимировнаНаписать 14484 29.08.2015

Номер материала: ДA-021380

29.08.2015 602

29.08.2015 741

29.08.2015 5744

29.08.2015 660

29.08.2015 1022

29.08.2015 1247

29.08.2015 347

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

530 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Первый мониторинг вузов РФ по новым показателям пройдёт в 2023 году

Время чтения: 2 минуты

В местах сдачи ЕГЭ будут применены антиковидные меры

Время чтения: 1 минута

Первые результаты по сокращению отчетности у учителей ожидаются осенью

Время чтения: 1 минута

Федеральный перечень учебников будет дополнен новыми учебниками

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

🎦 Видео